Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2004 Nov;20(4):367-95.
doi: 10.1123/jab.20.4.367.

Neuromusculoskeletal modeling: estimation of muscle forces and joint moments and movements from measurements of neural command

Thomas S Buchanan  1 , David G Lloyd, Kurt Manal, Thor F Besier
Affiliations

Neuromusculoskeletal modeling: estimation of muscle forces and joint moments and movements from measurements of neural command

Thomas S Buchanan et al. J Appl Biomech. 2004 Nov.

Abstract

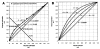
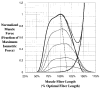
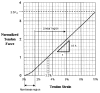
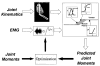
This paper provides an overview of forward dynamic neuromusculoskeletal modeling. The aim of such models is to estimate or predict muscle forces, joint moments, and/or joint kinematics from neural signals. This is a four-step process. In the first step, muscle activation dynamics govern the transformation from the neural signal to a measure of muscle activation-a time varying parameter between 0 and 1. In the second step, muscle contraction dynamics characterize how muscle activations are transformed into muscle forces. The third step requires a model of the musculoskeletal geometry to transform muscle forces to joint moments. Finally, the equations of motion allow joint moments to be transformed into joint movements. Each step involves complex nonlinear relationships. The focus of this paper is on the details involved in the first two steps, since these are the most challenging to the biomechanician. The global process is then explained through applications to the study of predicting isometric elbow moments and dynamic knee kinetics.

PubMed Disclaimer

Figures

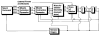
Figure 1
Figure 1
Forward dynamics approach to studying human movement. This flowchart depicts the neural command and forces for three muscles and the moments and joint angles for a two-joint system. As seen here, the three main steps require models of muscle activation dynamics, muscle contraction dynamics, and musculoskeletal geometry.
Figure 2
Figure 2
Inverse dynamics approach to studying human movement. This flowchart depicts the angular position for two joints, and the forces for three muscles. Note that the data processing flows from right to left.
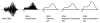
Figure 3
Figure 3
Muscle activation dynamics: Transformation from EMG to muscle activation.
Figure 4
Figure 4
Nonlinearization neural to muscle activation relationship: e(t) → a(t). (A) Dots represent data from Woods and Bigland-Ritchie (1983) for the biceps brachii for the isometric EMG-force relationship (demonstrating that other muscles showed a linear relationship), and the curves represent Equation 11. In this scheme, a perfectly linear relationship would fall on line A= 0. As values for A increase, a nonlinear region is added for lower force levels (left side of the A-line), while linear relationships continue for higher values (right side of the A-line). Point P marks where these two curves join. (B) Equation 12 is used to accomplish the same goals. Here the different shape factors, A, produce different curvature of the relationship. We limit A to be from −3<A<0, where 0 is a straight line.
Figure 5
Figure 5
(A) Schematic of muscle-tendon unit showing muscle fiber in series with the tendon. Note the pennation angle, φ, of the muscle fiber relative to the tendon and that the total tendon length, ℓt, is twice that of the tendon on either end of the muscle fiber, ℓt/2. (B) Schematic of muscle fiber with the contractile element and parallel elastic component. The nonlinear tendon stiffness is given by k. The force produced by the contractile element, Fm, is a function of ℓm and νm, while the tendon force, Ft, is a function of ℓt. The total muscle fiber force, Fm, is the sum of FAm and Fpm.
Figure 6
Figure 6
Normalized force-length relationship for muscle. Thick dark lines indicate maximum activation, whereas the light thin lines are lower levels of activation. Note that the optimal fiber length is longer as the activation decreases. In the figure, λ = 0.15, which means the optimal fiber length is 15% longer at zero activation.
Figure 7
Figure 7
Normalized force-length relationship for tendon (adapted from Zajac, 1989).
Figure 8
Figure 8
Flowchart of the modeling procedure. EMG is processed to obtain muscle activation while the position data is used to obtain musculoskeletal lengths, velocities, and moment arms. Together these are put into a Hill-type model to estimate musculotendon forces, and these in turn are multiplied by their moment arms and summed to obtain joint moment. This estimated moment is compared with the measured moment. In the optimization process, parameters in the model are adjusted to minimize the difference between measured and predicted joint moments. Once the parameters are tuned, the optimization part of the model is removed and it can now be used to predict joint moments for novel tasks.
Figure 9
Figure 9
Output of the model described in the section on Model Tuning and Validation. Values for elbow moment recorded experimentally are compared with those estimated by the model before model parameter adjustment and after optimization or tuning.
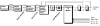
Figure 10
Figure 10
Hybrid Forward-Inverse dynamics approach to studying human movement and determining muscle forces for people performing tasks in movement laboratory. This simplified schematic depicts the angular position for one joint, and the forces for three muscles. Note that both the forward and inverse dynamics approaches provide estimates for joint moments, which can be used for validation of modeling.
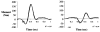
Figure 11
Figure 11
Typical results for predictions of knee joint moments from the calibrated Hybrid Forward-Inverse Dynamics approach: Crossover cut (left) and straight run (right). Thick line represents the EMG-driven model results; thin line represents the inverse dynamics results. (Adapted from Lloyd & Besier, 2003)
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. An KN, Takahashi K, Harrigan TP, Chao EY. Determination of muscle orientations and moment arms. Journal of Biomechical Engineering. 1984;106:280–282. - PubMed
    1. Anderson FC, Pandy MG. Dynamic optimization of human walking. Journal of Biomechical Engineering. 2001;123:381–390. - PubMed
    1. Bouisset, S. (1973). EMG and muscle force in normal motor activities Basel: Karger.
    1. Buchanan TS. Evidence that maximum muscle stress is not a constant: Differences in specific tension in elbow flexors and extensors. Medical Engineering and Physics. 1995;17:529–536. - PubMed
    1. Buchanan TS, Almdale DPJ, Lewis JL, Rymer, WZ Characteristics of synergic relations during isometric contractions of human elbow muscles. Journal of Neurophysiology. 1986;5:1225–1241. - PubMed
  NODES
Note 4
twitter 2