3D Finite Element Meshing from Imaging Data
- PMID: 19777144
- PMCID: PMC2748876
- DOI: 10.1016/j.cma.2004.11.026
3D Finite Element Meshing from Imaging Data
Abstract
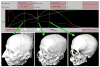
This paper describes an algorithm to extract adaptive and quality 3D meshes directly from volumetric imaging data. The extracted tetrahedral and hexahedral meshes are extensively used in the Finite Element Method (FEM). A top-down octree subdivision coupled with the dual contouring method is used to rapidly extract adaptive 3D finite element meshes with correct topology from volumetric imaging data. The edge contraction and smoothing methods are used to improve the mesh quality. The main contribution is extending the dual contouring method to crack-free interval volume 3D meshing with feature sensitive adaptation. Compared to other tetrahedral extraction methods from imaging data, our method generates adaptive and quality 3D meshes without introducing any hanging nodes. The algorithm has been successfully applied to constructing the geometric model of a biomolecule in finite element calculations.
Figures
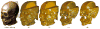
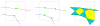

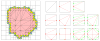
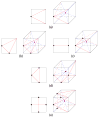

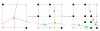










Similar articles
-
Adaptive and Quality Quadrilateral/Hexahedral Meshing from Volumetric Data.Comput Methods Appl Mech Eng. 2006 Feb 1;195(9):942-960. doi: 10.1016/j.cma.2005.02.016. Comput Methods Appl Mech Eng. 2006. PMID: 19750180 Free PMC article.
-
Feature-Sensitive Tetrahedral Mesh Generation with Guaranteed Quality.Comput Aided Des. 2012 May 1;44(5):400-412. doi: 10.1016/j.cad.2012.01.002. Comput Aided Des. 2012. PMID: 22328787 Free PMC article.
-
Quality Meshing of Implicit Solvation Models of Biomolecular Structures.Comput Aided Geom Des. 2006 Aug 1;23(6):510-530. doi: 10.1016/j.cagd.2006.01.008. Comput Aided Geom Des. 2006. PMID: 19809581 Free PMC article.
-
A voxel-based finite element model for the prediction of bladder deformation.Med Phys. 2012 Jan;39(1):55-65. doi: 10.1118/1.3668060. Med Phys. 2012. PMID: 22225275
-
A Robust Adaptive Mesh Generation Algorithm: A Solution for Simulating 2D Crack Growth Problems.Materials (Basel). 2023 Sep 29;16(19):6481. doi: 10.3390/ma16196481. Materials (Basel). 2023. PMID: 37834618 Free PMC article. Review.
Cited by
-
Continuum simulations of acetylcholine diffusion with reaction-determined boundaries in neuromuscular junction models.Biophys Chem. 2007 May;127(3):129-39. doi: 10.1016/j.bpc.2007.01.003. Epub 2007 Jan 19. Biophys Chem. 2007. PMID: 17307283 Free PMC article.
-
Influence of nonuniform geometry on nanoindentation of viral capsids.Biophys J. 2008 Oct;95(8):3640-9. doi: 10.1529/biophysj.108.136176. Epub 2008 Jul 11. Biophys J. 2008. PMID: 18621831 Free PMC article.
-
Variational Generation of Prismatic Boundary-Layer Meshes for Biomedical Computing.Int J Numer Methods Eng. 2009 Aug 20;79(8):907-945. doi: 10.1002/nme.2583. Int J Numer Methods Eng. 2009. PMID: 20161102 Free PMC article.
-
Patient-Specific Vascular NURBS Modeling for Isogeometric Analysis of Blood Flow.Comput Methods Appl Mech Eng. 2007 May 15;196(29-30):2943-2959. doi: 10.1016/j.cma.2007.02.009. Comput Methods Appl Mech Eng. 2007. PMID: 20300489 Free PMC article.
-
Automated measurement of heterogeneity in CT images of healthy and diseased rat lungs using variogram analysis of an octree decomposition.BMC Med Imaging. 2014 Jan 6;14:1. doi: 10.1186/1471-2342-14-1. BMC Med Imaging. 2014. PMID: 24393332 Free PMC article.
References
-
- Bajaj C, Coyle E, Lin KN. Arbitrary topology shape reconstruction from planar cross sections. Graphical Modeling and Image Processing. 1996;58(6):524–543.
-
- Bajaj C, Coyle E, Lin KN. Tetrahedral meshes from planar cross sections. Computer Methods in Applied Mechanics and Engineering. 1999;179:31–52.
-
- Bajaj C, Pascucci V, Schikore D. Fast isocontouring for improved interactivity. Proceedings of the IEEE Symposium on Volume Visualization. 1996:39–46.
-
- Bajaj C, Pascucci V, Schikore D. The contour spectrum. IEEE Visualization. 1997:167–174.
-
- Bajaj C, Wu Q, Xu G. ICES Technical Report. Vol. 301. The Univ. of Texas at Austin; 2002. Level set based volume anisotropic diffusion.
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
