Datei:01-Squaring the circle-Ramanujan-1914.gif

Originaldatei (778 × 714 Pixel, Dateigröße: 77 KB, MIME-Typ: image/gif, Endlosschleife, 32 Bilder, 2 min 49 s)
![]()
Diese Datei und die Informationen unter dem roten Trennstrich werden aus dem zentralen Medienarchiv Wikimedia Commons eingebunden.
Inhaltsverzeichnis
Beschreibung
| Beschreibung01-Squaring the circle-Ramanujan-1914.gif |
Deutsch: Quadratur des Kreises, Näherungskonstruktion nach Ramanujan von 1914, mit Weiterführung der Konstruktrion, Animation am Ende Pause 30 s
English: Squaring the circle, approximitiy construction according Ramanujan of 1914, with continuation of the construction, animation at the end pause 30 s |
| Datum | |
| Quelle | Eigenes Werk |
| Urheber | Petrus3743 |
| Andere Versionen |
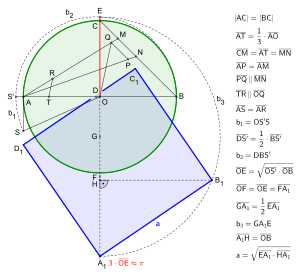 Squaring the circle, approximitiy construction according Ramanujan of 1914, with continuation of the construction |
Im Jahr 1914 ermittelte Ramanujan für eine noch genauere Quadratur als die von 1913, den folgenden Näherungswert für die Kreiszahl 
in dem acht Nachkommastellen mit denen von 
Ramanujan konstruierte in dieser Quadratur nicht die Seitenlänge des gesuchten Quadrates, es genügte ihm die Strecke OS darzustellen.[2] In der obigen Weiterführung der Konstruktion, wird die Strecke OS zusammen mit der Strecke OB zur Darstellung der mittleren Proportionalen (rote Strecke OG) herangezogen.[3]
Fehler
Bei einem Kreis mit Radius r = 1 [LE]:
- Konstruierte Seite des Quadrates a = 1,77245385062141... [LE]
- Soll-Seite des Quadrates as =
= 1,772453850905516... [LE]
- Absoluter Fehler = a - as = -0,00000000028411... = -2,841...E-10 [LE]
- Fläche des konstruierten Quadrates A = a2 = 3,14159265258265... [FE]
- Soll-Fläche des Quadrates As =
= 3,141592653589793... [FE]
- Absoluter Fehler = A - As = -0,000000001007143... = -1,007...E-9 [FE]
Beispiele zur Veranschaulichung der Fehlers
- Bei einem Kreis mit dem Radius r = 10.000 km wäre der Fehler der Seite a ≈ -2,8 mm
- Bei einem Kreis mit dem Radius r = 10 m wäre der Fehler der Fläche A ≈ -0,1 mm2
Error
In a circle of radius r = 1 [unit length, ul]:
- Constructed side of the square a = 1.77245385062141... [ul]
- _target side of the square as =
= 1.772453850905516... [ul]
- Absolute error = a - as = -0.00000000028411... = -2.841...E-10 [ul]
- Surface of the constructed square A = a2 = 3.14159265258265... [unit area, ua]
- _target area of the square As =
= 3.141592653589793... [ua]
- Absolute error = A - As = -0,000000001007143... = -1,007...E-9 [ua]
Examples to illustrate the errors:
- In a circle of radius r = 10,000 km would be the error of the side a ≈ -2.8 mm
- In the case of a circle with the radius r = 10 m would be the error of the surface A ≈ -0.1 mm2
Lizenz
- Dieses Werk darf von dir
- verbreitet werden – vervielfältigt, verbreitet und öffentlich zugänglich gemacht werden
- neu zusammengestellt werden – abgewandelt und bearbeitet werden
- Zu den folgenden Bedingungen:
- Namensnennung – Du musst angemessene Urheber- und Rechteangaben machen, einen Link zur Lizenz beifügen und angeben, ob Änderungen vorgenommen wurden. Diese Angaben dürfen in jeder angemessenen Art und Weise gemacht werden, allerdings nicht so, dass der Eindruck entsteht, der Lizenzgeber unterstütze gerade dich oder deine Nutzung besonders.
- Weitergabe unter gleichen Bedingungen – Wenn du das Material wiedermischst, transformierst oder darauf aufbaust, musst du deine Beiträge unter der gleichen oder einer kompatiblen Lizenz wie das Original verbreiten.
- ↑ S. A. Ramanujan: Modular Equations and Approximations to π In: Quarterly Journal of Mathematics. 12. Another curious approximation to π is, 43, (1914), S. 350–372. Aufgelistet in: Published works of Srinivasa Ramanujan Abgerufen am 21. November 2016
- ↑ Modular Equations and Approximations to π In: Quarterly Journal of Mathematics. 12. Another curious approximation to π is ... Fig. 2, 44, (1914), S. 350–372. Aufgelistet in: Published works of Srinivasa Ramanujan Abgerufen am 21. November 2016
- ↑ Universität Magdeburg A.14 Mittelwerte. Mittlere Proportionale, Seite 2 (PDF-Datei) Abgerufen am 21. November 2016
Kurzbeschreibungen
In dieser Datei abgebildete Objekte
Motiv
Einige Werte ohne einen Wikidata-Eintrag
21. November 2016
image/gif
e307c4a46a81fa185b7d44d75b9922152fdde18a
79.204 Byte
169 Sekunde
714 Pixel
778 Pixel
Dateiversionen
Klicke auf einen Zeitpunkt, um diese Version zu laden.
| Version vom | Vorschaubild | Maße | Benutzer | Kommentar | |
|---|---|---|---|---|---|
| aktuell | 14:04, 25. Dez. 2016 |  | 778 × 714 (77 KB) | Petrus3743 | ≈ π ergänzt |
| 12:08, 25. Dez. 2016 |  | 778 × 714 (77 KB) | Petrus3743 | Konstruktion vereinfacht | |
| 12:13, 9. Dez. 2016 |  | 883 × 826 (82 KB) | Petrus3743 | Kurzbeschreibung korrigiert | |
| 19:38, 21. Nov. 2016 |  | 883 × 826 (95 KB) | Petrus3743 | User created page with UploadWizard |
Dateiverwendung
Keine Seiten verwenden diese Datei.
Metadaten
Diese Datei enthält weitere Informationen (beispielsweise Exif-Metadaten), die in der Regel von der Digitalkamera oder dem verwendeten Scanner stammen. Durch nachträgliche Bearbeitung der Originaldatei können einige Details verändert worden sein.
| GIF-Dateikommentar | Created with GIMP |
|---|
![{\displaystyle \pi \approx {\sqrt[{4}]{9^{2}+{\frac {19^{2}}{22}}}}=3{,}141592652\dots }](https://wikimedia.org/api/rest_v1/media/math/render/svg/a8181d220358716c2f95c2bbc5cf5ba3e2b2e686)