Abstract
The recognition and content analysis of the components in petrographic thin section image is a valuable study in geology. In this paper, we propose a two-stage method to segmentation and recognition of petrographic thin section image. In the first stage, we propose an image segmentation algorithm that can adaptively generate superpixel numbers based on SLIC algorithm. The algorithm is able to continually correct the number of superpixels in the iteration and then cluster the pixels of the image into superpixels by both color and spatial features. In the second stage, we designed a convolutional neural network and trained it with mineral grain images, which is then used to classify the superpixels obtained by first-stage. Finally, we count the categories and content of the components in the image based on the segmentation and classification results. We collected some images and invited geologists to label them for experimentation. The experimental results demonstrate the following: (1) Our proposed image segmentation algorithm is capable of dynamically generating the superpixels by the number of mineral grains in the image. (2) The CNN model we designed can accurately identify the categories of superpixel regions and has a small size. (3) The two-stage method is very effective in identifying the category of major components in an image and accurately estimating the content.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
The recognition and analysis of petrographic thin section plays an important role in the development of oil and gas resources. The traditional method of recognizing petrographic thin section is to cut and grind them into tens of micrometers of thin section, and then the researchers analyzes the image under the microscope [1]. Traditional methods require the knowledge of a researcher to complete, and the analysis of rock composition is cumbersome, time-consuming, and inaccurate. With the rapid development of digital image processing, image recognition technology has been widely used in petrographic thin section analysis. Segmentation and recognition of mineral grains in thin section images by image segmentation and recognition algorithms can accurately measure the categories and contents of major components in rock samples, thus better assisting petroleum development.
Because rock samples are usually formed by the bonding of mineral grains, there is a good idea for the analysis of the composition of petrographic thin section images. Using the image segmentation algorithm to segment the grains in the image and then identify each grain, the category and content of the main components in the thin section can be counted. In principle, almost all existing image segmentation algorithms can be used in the automatic segmentation of grain, such as region growing [2], ERS [3] and TurboPixel [4]. However, these algorithms are designed for ordinary scene images and may not be suitable for processing petrographic thin section image which contains large numbers of mineral grains. The superpixel segmentation algorithm is an image region over-segmentation algorithm. The image is divided into multiple irregular image blocks according to certain feature similarities. The current effective algorithm are LSC [5], SEEDS [6], SLIC [7] and so on. We believe that the sub-regions subdivided by the superpixels are similar to the contours of the mineral grains, so the superpixels obtained by the segmentation can be identified as a single grain. For example, Jiang et al. [8, 9] used a superpixel algorithm to segment and merge sandstone thin section images to obtain the contours of sandstone grains. However, the currently existing superpixel algorithm is very inefficient, or it is necessary to set the number of superpixels desired in advance. Therefore, we propose an algorithm that is fast and can dynamically adjust the number of superpixels based on the number of grains in the image.
After the image is segmented, the segmented sub-regions need to be identified. Since the crystal grains constituting the rock are generally colorless and transparent and have similar refractive indices, adjacent grains exhibit similar colors under a plane polarizing microscope, and it is sometimes difficult for the human eye to discern the difference. Unlike plane polarized light images, grains produce different interference colors under orthogonally polarized light [10]. For example, quartz and feldspar in sandstones require experts to combine orthogonal polarized and plane polarized images to distinguish them [11]. In recent years, convolutional neural networks have achieved remarkable success in a lots of computer vision tasks, such as image recognition [12, 13], object detection [14] and semantic segmentation [15]. Therefore, we have designed a CNN model that can combine the orthogonal polarized and plane polarized images to identify the sub-regions obtained by the previous segmentation. After identifying the category of each sub-regions, the area of each sub-regions of each category is counted, and the categories and contents of the major components in the image can be approximated.
In this paper, we have mainly completed the following work: (1) We propose a two-stage method to identify the major components of petrographic thin section. In the first stage, the image is segmented into over-segmented superpixel images. In the second stage, the CNN model is trained to identify each superpixel region to obtain the category of the mineral grain to which each superpixel region belongs. (2) We have enhanced the SLIC algorithm and proposed an algorithm that can generate superpixel adaptively based on the number of mineral grains in the image. For different images, our algorithm only needs to set a fixed \( K \) value, and the algorithm can dynamically adjust the number of superpixels to be segmented in multiple iterations. (3) We designed a CNN model that effectively classifies mineral grains that are common in petrographic thin section images. The CNN model can receive orthogonal polarized and plane polarized images as inputs, and can adapt to any size. (4) We created a dataset that included thousands of petrographic thin section images. The details of the dataset are described in Sect. 2.3.
2 Proposed Method
The compositional analysis of the petrographic thin section image is divided into two stage. In the first stage, we proposed the SLIC method of adaptive superpixel number (AS-SLIC). The AS-SLIC algorithm can adaptively generate multiple superpixels based on the number and characteristics of mineral grains in the image. In the second stage, the CNN is trained to identify the superpixels obtained by the previous stage. By identifying the category of mineral grains in each superpixel region, the approximate content of the major components in each thin section image can be calculated.
2.1 The SLIC of Adaptive Superpixel Number (AS-SLIC)
We first introduce the original SLIC algorithm. The original SLIC superpixels correspond to clusters in the CIELAB color space and spatial space. First, the algorithm needs to set two values \( m \) and \( K \), \( m \) is a constant value, and \( K \) represents the number of superpixels that are desired to be divided. Then, the image is divided into \( K \) grids, and the center point of each grid is used as the initial cluster \( C_{k} = \left[ {l_{k} ,a_{k} ,b_{k} ,x_{k} ,y_{k} } \right]^{T} \). A pixel \( P_{i} \) color is represented in the CIELAB color space \( \left[ {l,a,b} \right]^{T} \), as shown in Eq. (1), the \( d_{c} \) is color distance between \( P_{i} \) and \( C_{k} \). The \( \left[ {x,y} \right]^{T} \) represents the position of the pixel. As shown in Eq. (2), the \( d_{s} \) represents the spatial space distance between \( P_{i} \) and \( C_{k} \). The \( D_{dist} \) computes the distance between \( P_{i} \) and \( C_{k} \) is measured in both color and spatial space, which is defined as Eq. (3). In the Eq. (3), \( S = \sqrt {N/K} \), where \( N \) is the number of pixels of the input image. Since the initial superpixel approximates an \( S \times S \) region, the search for similar pixels is done in a region \( 2S \times 2S \) around the cluster center. In one iteration, each pixel is assigned to the nearest cluster center, then the new cluster center is recalculated and the next iteration continues.
In the petrographic thin section image especially the sandstone thin section image, the mineral grains of different origins are different in size, so the number of grains in the image varies from tens to hundreds. The original SLIC algorithm needs to set the number of superpixels divided in advance. When the number of mineral grains in the image is large, setting a smaller \( K \) will cause a superpixel to contain multiple grains. Conversely, if the number of grains in the image is small, setting a larger \( K \) will cause over-segmentation. Both of the above cases are not conducive to subsequent classification. As shown in Fig. 2(a), we use the original SLIC algorithm and set \( K \) to 20. The results on the left Fig. 2(a) are acceptable, but because the grain area in the right of Fig. 2(a) is small, many superpixels contain multiple grain regions.
We proposed AS-SLIC algorithm takes into account the properties of mineral grains in petrographic thin section image. Most of the mineral grain composition is relatively single, so a single grain exhibits a uniform color in the image. Because of the optical properties of the crystals that make up the mineral grains, the differently oriented grain will show different colors under an orthogonal polarizing microscope. When a plurality of grain regions are included in one superpixel obtained by the segmentation, the superpixel will present a plurality of regions of different colors. So we can use the color histogram of all the pixels in the superpixel to determine whether the superpixel contains only a single grain. As shown in Fig. 1(a), this superpixel contains two grain regions, so the gray histogram of the superpixel has two peaks as shown in Fig. 1(b).
Our method still needs to set \( K \) at the beginning, and \( K \) represents the number of cluster centers in the first iteration. Because the number of cluster centers will gradually increase during the iteration, the initial set \( K \) value is relatively small. In the original SLIC algorithm, once each pixel has been assigned to the appropriate cluster, then the mean vector of all the pixels belonging to each cluster are recalculated to update the cluster center. The difference between the algorithm we designed and the original SLIC lies in the update strategy of the cluster center. First, for each cluster center, the gray histogram \( H_{k} \) of all the pixels belonging to the cluster is counted. If the resulting gray histogram has only one peak, then it is likely that only one whole grain or a local region of one grain is included in the cluster. In this case, the average vector \( V_{k}^{i} = \left[ {l_{i} ,a_{i} ,b_{i} ,x_{i} ,y_{i} } \right]^{T} \) of all the pixels belonging to this cluster \( C_{k} \) is used as the new cluster center \( C_{k}^{{\prime }} \), as shown in the Eq. (4). If the gray histogram has two or more peaks, the pixels belonging to this cluster \( C_{k} \) are from multiple grain regions. Therefore, it is necessary to split the cluster \( C_{k} \) into multiple cluster. It is assumed that there are \( T \) peaks in the gray histogram \( H_{k} \), the corresponding gray value at the peak is represented by \( Peak_{i} \), and \( V_{k}^{j} \) represents a vector of pixels in the cluster \( C_{k} \) whose gray value is equal to \( Peak_{i} \). The previous cluster \( C_{k} \) is split into \( T \) new cluster according to peak. The calculation method of the new cluster \( C_{k}^{i} \) is as shown in the Eq. (5), where \( m \) represents the number of pixels in the cluster center \( C_{k} \) whose gray value is equal to \( Peak_{i} \).
In order to avoid a superpixel splitting too many sub-regions, in each iteration we only select the two peaks containing the largest number of pixels in \( H_{k} \) to split. And in the experiment we set a maximum value \( K_{max} \), when the number of cluster in the iteration is greater than \( K_{max} \), the splitting strategy is no longer executed. We use \( L_{2} \) norm shown in Eqs. (6) and (7) to compute the residual error \( R \) between the new cluster and previous cluster locations. The iteration is stopped when \( R \) is less than a certain threshold. The entire algorithm is shown in Table 1.
2.2 Classification of Mineral Grains
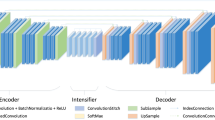
Convolutional neural networks have been used for classification tasks for many years. Therefore, we designed a CNN model to identify the superpixel region obtained by the first stage segmentation. The orthogonal polarized image of the thin section focuses on the color features of the rock, and the plane polarized image focuses on the texture features of the rock. In order to make full use of the information in plane polarized and orthogonal polarized images, and to adapt to the superpixels of various sizes as input, we designed the CNN model to combine depthwise separable convolution [16] and spatial pyramid pooling [17].
Our CNN model architecture is shown in Table 2. The input to the model is two images, which are the orthogonal polarized image \( I_{o} \) and the plane polarized image \( I_{p} \) of the rock thin section. We expect the model to extract specific low-level semantic features from the two images, respectively. In the first input layer, the input \( I_{o} \) and \( I_{p} \) are group convolved with a 3 × 3 × 3 × 32 convolutional filter. The layer in front of the model uses a depth separable convolution, which is computationally intensive and leaves no information to communicate between the two images entered. After extracting the low-level semantic features from the two images, in order to combine the features in the two images to obtain the high-level semantic features of the rock sample as a whole, the \( 1 \times 1 \) pointwise convolution is used for information exchange. All layers are followed by a ReLU nolinearity and batchnorm. Down sampling is handled with strided convolution in the depthwise convolutions.
Since the size of the superpixel obtained in the first stage is uncertain, and in order to prevent loss of features due to image scaling, we hope that the model can accept superpixel regions of any size or scale as input. Therefore, our model uses the strategy of spatial pyramid pooling to produce a fixed-size representation. There are two fully connected layers after the spatial pyramid pooling layer and feeds into a softmax layer for classification. To prevent overfitting, the dropout strategy is used and the value is set to 0.3. Finally, cross entropy loss is employed as the loss function to train the network. Counting convolutions and fully connected layers, our model has 28 layers.
2.3 Image Dataset
To verify the effect of our method on petrographic thin section images, we collected the images and invited geologists to mark them. First, we created the Petrographic Thin Section Image Dataset (PTSID). The PTSID includes images of 801 rock samples in 7 categories, each sample with a plane polarized image and a orthogonal polarized image. So there are 1602 images in the PTSID, and the resolution of each image is \( 1392 \times 1040 \) pixels. Each image is detailed with the category of sample, the category and content of the main components (the content is expressed as a decimal, and the sum of the components is 1). There are 500 images in the PTSID that are pixel-level annotations for typical mineral grains, with a total of 2126 mineral grains in 21 categories. To train the CNN model we designed, we also produced the Mineral Grain Classification Dataset (MGCD). The mineral grain region marked in the PTSID is first extracted to generate a sub-image whose size is equal to the minimum circumscribed rectangle of the grain contour. In addition to the grain region in the sub-image, the pixel values of the other regions are filled with 0. The sub-image is then rotated, scaled, and cropped to augment the dataset. In order to maintain data balance between categories, we rotate the categories with fewer images to rotate more angles to get more new images. After the above process, a total of 8150 mineral grain images in 21 categories were included in the MGCD.
3 Experiments
3.1 Superpixel Segmentation Experiment
We selected sandstone thin section images from PTSID to verify the performance of the AS-SLIC algorithm. The reason for selecting the sandstone image is that it contains a large number of grains of different sizes, which can reflect the characteristics of the algorithm adaptively generating the number of superpixels. Figure 2 shows a comparison of our AS-SLIC with the original SLIC. The initial \( K \) values of both algorithms are set to 20. As shown in the right column of Fig. 2, when the number of grains in the image is large, the superpixels segmented by the original SLIC contain multiple grains, which is not as good as our AS-SLIC. Obviously, our algorithm can generate different superpixel number segmentation results for different images.
In terms of performance, we have found that majority of the image clusters do not change after 4 iterations. After 11 iterations, the residual error \( R \) of most images will be less than the threshold. Therefore, the time complexity of our algorithm in practical applications is close to that of the SLIC algorithm. We experimented with an image with a resolution of \( 1392 \times 1040 \). The average computational complexity of our AS-SLIC and other existing superpixel algorithms is shown in Table 3. Because our algorithm needs to count the gray histogram in the iteration, and the number of clusters may increase, it takes more time than the original SLIC algorithm. However, compared to other classic superpixel algorithms such as GC [18], TP [4] and QS [19], our algorithm is still very fast.
3.2 Image Classification Result
Training Methods.
Our model was built on the TensorFlow framework and was trained using the GTX 1080 GPU. We used the “Xavier” algorithm [20] to initialize the weights of all layers. The initial learning rate was 0.001 and reduced to \( \sqrt {0.1} \) every 10 epochs. The training used stochastic gradient descent with 0.9 momentum. The batch size was set to 32 and the training “early stopping” (When the loss of the training set in five consecutive epochs is no longer reduced, the training is stopped) strategy is used. We use the “Multi-Size Training” strategy [17] mentioned in SPPNet for training. We resize the training set to four scales \( {\text{s}} = \left\{ {224,192,160,128} \right\} \) and randomly selected one scale image for training in each epoch.
Results and Analyses.
Our CNN model and other popular models were tested on the MGCD dataset. Table 4 compares our model to the VGG16 [21], ResNet [13], GoogLeNet [22] and MobileNet [16]. Overall, the ResNet34 model has the highest accuracy. This may be because the color and texture features in the thin section image are easily lost after multi-layer convolution, and the “shortcut connection” structure in the ResNet model makes the low-level information easier to forward propagation. Although the VGG model has the largest parameter, it is easier to overfit and the gradient disappears, so the performance is the worst. Our model is nearly as accurate as ResNet and is the smallest one of all models. Compared with the MobileNet and GoogLeNet models of the light weight, our model has the highest accuracy and the smallest model size. This shows that our model architecture is suitable for processing petrographic thin section images.
3.3 Analysis of Components
We summarize the results of the classification of each superpixel in the second stage, and the sum of the areas of the superpixel regions of each category is taken as the content of the mineral grains. As shown in Fig. 3, and 3(a) is a petrographic thin section image, and Fig. 3(b) is the segmentation and recognition result of Fig. 3(a). Each superpixel in the image covers an entire mineral grain or a part of a mineral grain, so the recognition result of the superpixel can be used as the category of the mineral grain. The different categories of mineral grains identified in the image are represented by different colors, and the percentage of each category of grains in the entire sample is counted. The results of the component analysis in this experiment were reviewed by several geologists. Experts believe that our analysis results are close to the results of manual analysis, and have a good application prospect, which provides a good solution for the automated analysis of petrographic thin section images in the future geology field.
3.4 Computation Cost
Our method is implemented using Python3.6 and Tensorflow1.12 on a PC with an GTX1080 GPU card (8 GB RAM) and Intel Core i7 3.6 GHz. The average processing time for an image with \( 1392 \times 1040 \) resolution is 8.9 s. In the first-stage, since only the CPU was used for calculation, the average time was 7.1 s. In the second-stage, the superpixel region was identified using 1.7 s, and finally the statistics were consumed for 0.1 s. It can be seen that the first stage consumes a lot of time, and in our future research, implementing our superpixel segmentation algorithm as an algorithm that can be executed in parallel on the GPU can achieve faster execution efficiency.
4 Conclusion
In this paper, we propose a two-stage method for recognizing the category and content of the major components in the petrographic thin section image. We proposed an AS-SLIC algorithm, which adaptively adjusts the number of superpixels according to the gray histogram of the superpixel in each iteration. In the experiment, our AS-SLIC algorithm maintains the same speed as the original SLIC algorithm. When the number of grains in the image is large, it can adaptively increase the number of superpixels, and the generated superpixel is more suitable for the edge of the grain. We designed a CNN model to identify mineral grains that showed excellent performance in our MGCD dataset. Our model is a light weight network and has the same excellent classification results as other classic models such as ResNet. The results of our two-stage method for the analysis of petrographic thin section image were recognized and praised after evaluation by several geologists. Our method has important reference value for component analysis in other types of images, such as cancer cell analysis in medical images, remote sensing image analysis, and so on.
References
Tetley, M.G., Daczko, N.R.: Virtual Petrographic Microscope: a multi-platform education and research software tool to analyse rock thin-sections. Aust. J. Earth Sci. 61(4), 631–637 (2014)
Izadi, H., Sadri, J., Mehran, N.A.: A new intelligent method for minerals segmentation in thin sections based on a novel incremental color clustering. Comput. Geosci. 81, 38–52 (2015)
Liu, M.Y., Tuzel, O., Ramalingam, S., Chellappa, R.: Entropy rate superpixel segmentation. In: IEEE Conference on Computer Vision and Pattern Recognition (CVPR), pp. 2097–2104. IEEE (2011)
Levinshtein, A., Stere, A., Kutulakos, K.N., et al.: Turbopixels: fast superpixels using geometric flows. IEEE Trans. Pattern Anal. Mach. Intell. 31(12), 2290–2297 (2009)
Li, Z., Chen, J.: Superpixel segmentation using linear spectral clustering. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), pp. 1356–1363. IEEE (2015)
Bergh, M.V.D., Boix, X., Roig, G., et al.: SEEDS: superpixels extracted via energy-driven sampling. In: Fitzgibbon, A., Lazebnik, S., Perona, P., Sato, Y., Schmid, C. (eds.) ECCV 2012. LNCS, vol. 7578, pp. 13–26. Springer, Heidelberg (2012). https://doi.org/10.1007/s11263-014-0744-2
Achanta, R., Shaji, A., Smith, K., et al.: SLIC superpixels compared to state-of-the-art superpixel methods. IEEE Trans. Pattern Anal. Mach. Intell. 34(11), 2274–2282 (2012)
Jiang, F., Gu, Q., Hao, H.Z., et al.: Grain segmentation of multi-angle petrographic thin section microscopic images. In: IEEE International Conference on Image Processing (ICIP), pp. 3879–3883. IEEE (2017)
Jiang, F., Gu, Q., Hao, H.Z., et al.: Feature extraction and grain segmentation of sandstone images based on convolutional neural networks. In: 2018 24th International Conference on Pattern Recognition (ICPR), pp. 2636–2641. IEEE (2018)
Tarquini, S., Favalli, M.: A microscopic information system (MIS) for petrographic analysis. Comput. Geosci. 36(5), 665–674 (2010)
Asmussen, P., Conrad, O., Gnther, A., et al.: Semi-automatic segmentation of petrographic thin section images using a seeded-region growing algorithm with an application to characterize wheathered subarkose sandstone. Comput. Geosci. 83, 89–99 (2015)
Krizhevsky, A., Sutskever, I., Hinton, G.E.: ImageNet classification with deep convolutional neural networks. In: Proceedings of Advances in Neural Information Processing Systems, Lake Tahoe, pp. 1097–1105 (2012)
He, K., Zhang, X., Ren, S., et al.: Deep residual learning for image recognition. In: IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, pp. 770–778 (2016)
Girshick, R., Donahue, J., Darrell, T., et al.: Rich feature hierarchies for accurate object detection and semantic segmentation. In: IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Columbus, pp. 580–587 (2014)
He, K., Gkioxari, G., Dollár, P., et al.: Mask R-CNN. arXiv preprint arXiv:1703.06870 (2017)
Howard, A.G., Zhu, M., Chen, B., Kalenichenko, D., et al.: MobileNets: efficient convolutional neural networks for mobile vision applications. arXiv preprint arXiv:1704.04861 (2017)
He, K., Zhang, X., Ren, S., Sun, J.: Spatial pyramid pooling in deep convolutional networks for visual recognition. IEEE Trans. Pattern Anal. Mach. Intell. 37(9), 1904–1916 (2015)
Veksler, O., Boykov, Y., Mehrani, P.: Superpixels and supervoxels in an energy optimization framework. In: Daniilidis, K., Maragos, P., Paragios, N. (eds.) ECCV 2010. LNCS, vol. 6315, pp. 211–224. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-15555-0_16
Vedaldi, A., Soatto, S.: Quick shift and kernel methods for mode seeking. In: Forsyth, D., Torr, P., Zisserman, A. (eds.) ECCV 2008. LNCS, vol. 5305, pp. 705–718. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-88693-8_52
Glorot, X., Bengio, Y.: Understanding the difficulty of training deep feedforward neural networks. In: 13th International Conference on Artificial Intelligence and Statistics, vol. 9, pp. 249–256 (2010)
Simonyan, K., Zisserman, A.: Very deep convolutional networks for large-scale image recognition. arXiv preprint arXiv:1409.1556 (2014)
Szegedy, C., Liu, W., Jia, Y., et al.: Going deeper with convolutions. In: IEEE Conference on Computer Vision and Pattern Recognition (CVPR), pp. 1–9. IEEE (2015)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
Dong, L., Zhang, Z. (2019). A Method for Analyzing the Composition of Petrographic Thin Section Image. In: Zhao, Y., Barnes, N., Chen, B., Westermann, R., Kong, X., Lin, C. (eds) Image and Graphics. ICIG 2019. Lecture Notes in Computer Science(), vol 11901. Springer, Cham. https://doi.org/10.1007/978-3-030-34120-6_40
Download citation
DOI: https://doi.org/10.1007/978-3-030-34120-6_40
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-34119-0
Online ISBN: 978-3-030-34120-6
eBook Packages: Computer ScienceComputer Science (R0)