Introduction

The Leaf Area Index (LAI) is an ecophysiology key parameter characterising the canopy-atmosphere interface where most of the energy fluxes are exchanged. It is related to several vineyard environmental conditions, such as terrain erosion rates, soil organic carbon problems and climate change effects (Rodrigo-Comino 2018). Detailed LAI maps would be valuable for growers, who could use them to optimise decisions and crop management on the basis of available spatial and temporal LAI information. LAI evaluation is thus crucial in viticulture, although the procedures for its assessment are generally laborious and provide information within limited areas. For this reason, producing maps for managing the spatial and temporal variability of the LAI in large croplands with traditional techniques is difficult. New cost-effective, easy and reliable methods for evaluating the LAI on extended regions, with high spatial and temporal resolutions, are thus required. In this work, an innovative methodology to estimate the LAI on extended vineyards is presented. The proposed approach exploits dense 3D point clouds generated by processing UAV-based multispectral imagery by using the structure from motion method. An experiment on a vineyard in Serralunga d’Alba (Piedmont, Northwest of Italy) showed the correlation between the estimated LAI from 3D point cloud and traditional manual measurement.

New systems for crop management are being designed to increase yield and farm production efficiency while reducing resources consumption and impact on the environment (Zhang et al. 2018). In this context, precision agriculture is an essential approach that uses information technology and specialised hardware to perform site-specific crop management in order to deal with spatial and temporal crop variability (Zaman et al. 2019; González Perea et al. 2018; Grella et al. 2017).

Effective precision agriculture techniques rely on detailed and reliable cropland status mapping tools, such as representing weed distribution (Torres-Sospedra and Nebot 2014), missing plants (Primicerio et al. 2017), crop typology (Suh et al. 2018), soil properties (Quebrajo et al. 2018; Näsi et al. 2017), plant water stress (Khanal et al. 2017), vigour (Ampatzidis and Partel 2019; Primicerio et al. 2015), crop layouts (Comba et al. 2015) and nutrients assessment (Corti et al. 2018; Pimstein et al. 2011). Remote sensing by airborne and/or ground devices is a valuable technology that is able to rapidly create reliable and accurate maps of extended cropland by exploiting the different spectral reflectance of crops depending on their status (Quebrajo et al. 2018; Khanal et al. 2017). Among air vehicles, small UAVs have become widely used for remote sensing in precision agriculture applications due to their versatility and adaptability to the needs of the user, field morphology and applications, providing an imagery characterised by high spatial and temporal resolutions (Barrero and Perdomo 2018; Jin et al. 2017; Gago et al. 2015; Vega et al. 2015).

Information from remote sensing can be used to evaluate several indices regarding vegetation status, with Leaf Area Index (LAI) being one of the widely exploited biophysical indices (Córcoles et al. 2013). The LAI, a dimensionless parameter defined as the one-side leaf area per unit ground area (Watson 1947), directly accounts for the interactions between crops and atmosphere, in terms of photosynthesis, transpiration and solar radiation interception (Cotter et al. 2017).

In-field direct and indirect methods for LAI assessment (Jonckheere et al. 2004) include procedures done by trained operators on one or more plants (Qu et al. 2016; Schirrmann et al. 2015). These methods are usually very labour-intensive and time-consuming, making the measuring procedure unsuitable for large numbers of plants and/or extensive cropland, and requires specific approaches in order to obtain reliable measures from pointwise assessments (Martinez et al. 2012). Modern techniques for LAI estimation based on proximal sensing, such as conventional digital cameras (Mora et al. 2016), a set of RGB fisheye cameras (Zarate-Valdez et al. 2012) or thermal imaging (Banerjee et al. 2018), even improving reliability and velocity of LAI assessment, still provide pointwise estimation. In this context, remote sensing represents a favourable technique that can be used to rapidly estimate the LAI within crop areas, such as by airborne laser scanning (Pearse et al. 2017) or multispectral cameras (Herrmann et al. 2019). Satellite-derived LAI products are also available (Copernicus Global Land Service 2019; Johnson et al. 2003), with some limitations in specific applications (Khaliq et al. 2019; Liu et al. 2018a; Mannschatz et al.; 2014).

Recently, accurate 3D crop models (i.e. 3D point clouds) have led to innovative features for crop phenotyping. Point cloud models, large datasets of points representing the surface of visible objects, can be directly provided by laser scanning (such as light detection and ranging systems—LiDAR) (Sanz et al. 2018; Bietresato et al. 2016; Koening et al. 2015; Arnó et al. 2013) or derived from multispectral imagery by photogrammetry and computer vision algorithms such as, for example, structure from motion (Patrick and Li 2017; Jay et al. 2015; Zarco-Tejada et al.; 2014; Guillen-Climent et al. 2012). However, in the case of complex and irregular objects made of partially overlapping items, like crop canopy structures, the quality of the 3D point cloud reconstruction is a relevant aspect to be taken into account (Liu et al. 2018b). Several studies have confirmed the reliability and effectiveness of evaluating the crop phenotype from dense 3D point clouds (Mortensen et al. 2018; Patrick and Li 2017; Lati et al. 2013), leaves shape and distribution (Li and Tang 2017; Jay et al. 2015), branches (Li and Tang 2017), and fruit zone architecture (Schöler and Steinhage 2015). The cited research works have not investigated only external crop features, like crop height and canopy volume, but also intra-canopy characteristics of the monitored crop. Although those studies have provided promising results and showed that crop canopy can be properly and detailly modelled in detail by 3D point cloud model, they were mainly conducted in the laboratory and/or focused on few specific plants. A preliminary 3D point cloud processing method to estimate LAI on an extensive crop field was presented by Mathews and Jensen (2013), but the results were influenced by the low density of the point cloud. Thus, retrieval of plant structural parameters from 3D models derived by structure from motion processing techniques shows an interesting potential for the development of precision agriculture tools.

The objective of this paper is to evaluate the reliability of LAI estimation by processing dense 3D point clouds as a cost-effective alternative to traditional LAI assessments. This would allow for high resolution, extensive and fast mapping of the index, even in hilly and not easily accessible regions. In this setting, the 3D point clouds were generated from UAV-based multispectral imagery and processed by using an innovative methodology presented here. The LAI was estimated by a multivariate linear regression model using crop canopy descriptors derived from the 3D point cloud, which account for canopy thickness, height and leaf density distribution along the wall.

Materials and methods

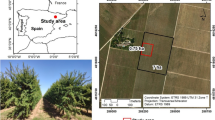
A vineyard located in Serralunga d’Alba (Piedmont, Northwest of Italy) was selected as the study site. It included three contiguous parcels cultivated with Cv. Nebbiolo grapevine covering a total surface of about 2.5 ha. The area is located at approximately 44°62′4″ latitude and 7°99′9″ longitude ({WGS84} reference system) while the elevation ranges from 330 to 420 m above sea level. A loamy soil and a steep slope (ranging from about 8 to 30%) characterise the vineyard, which is exposed towards the southeast (ranging from 120° to 160°) with the vine rows perpendicular to the maximum slope gradient. Due to the irregularity of the vineyard terrain morphology in terms of altitude, soil features and inclination, the vine vigour usually varies within and between parcels. Indeed, vine vigour is influenced by the pedological variability connected to the potentially different availability of water and organic matter in the soil (Rodrigo-Comino et al. 2016). This induces high variability in terms of canopy micro-climatic conditions that obliges the growers to modulate agronomic interventions to achieve high-quality vine standards.

An experiment was conducted during 2017 and 2018 to assess the seasonal development of the vine canopy. In-field LAI measurements and UAV flights were performed on 6 dates. Table 1 reports the dates and the phenological phases at which the experimental campaign was performed.

Table 1 Dates and phenological phases (Meier 2001) at which the experimental campaign was performed
Full size table

Leaf surface varies during the phenological cycle: in Piedmont, it is at its minimum after bud break (April), achieves its peak in the central part of the season (June–July) and decreases during the final phase of grape ripening.

Point cloud generation

Six 3D point clouds of the study site were generated from aerial multispectral image blocks of more than 1000 images each and were acquired with a Parrot Sequoia® multispectral camera (Parrot© SA, 2018). The UAV flights were planned to maintain a flight height of about 35 m with respect to the terrain and to assure an overlapping between adjacent images greater than 80%, with a frame rate acquisition of 1 Hz. With these defined flight parameters, the UAV path required about 30 min flights to cover the study site (2.5 ha) and the ground sample distance of aerial images was 5 cm. The UAV flights were performed as close as possible to noon to reduce shadowing between vines rows. Aerial image blocks were processed with Agisoft PhotoScan® software (Agisoft©, 2018) to generate the 3D point clouds. A radiometric calibration was applied to the image blocks by using reference images of a Micasense calibrated reflectance panel, acquired before and after each UAV flight. The average density of the 3D point clouds is about 1450 points per m2 of site surface. To georeference the 3D point clouds in the {WGS84} reference system, the position of 12 markers located within the three parcels were measured with a differential GNSS system. To allow their visibility from the airborne sensor, markers were placed on the top of the vine trellises, the positions of which were properly chosen to obtain an equidistant distribution within the selected vineyard.

In-field LAI measurements

A set of vineyard blocks, made of 8 vines each and about 8 m long, were selected in the three parcels for the in-field measurements looking for vigour heterogeneity. The estimation of the leaf area per vine, performed by using the indirect method of inclined point quadrat (Wilson 1963), involved 704 vines. The PQ method has been widely used for viticultural purposes (Silvestroni et al. 2018) and was shown to be a reliable method as a standard reference for the assessment of total vine leaf area (Smart and Robinson 1991). Indeed, a high correlation between the PQ results and those obtained by methods that directly measure the vine leaf area was demonstrated (Vitali et al. 2013). To calculate the LAI index, the soil surface on which the plants stand on was taken into account. The PQ method was applied by inserting a thin cane inside the vegetation at three different wall canopy heights (70, 130, 190 cm from the ground level). The cane was inserted every 20 cm along the wall canopy of the selected vineyard blocks for about 120 insertions every eight plants. The cane insertion allows the interception of a number of leaves equal, on average, to the number of leaf layers and, therefore, leaf density. The thickness and height of the canopy were measured simultaneously. The total leaf area per plant (m2) was obtained by multiplying the leaf layer number by both the leaf wall height and the space between vines. The in-field LAI measurements involved 88 vineyard blocks. The position of the vineyard blocks’ endpoints \(a_{\text{j}}^{{\left\{ {{\text{WGS}}84} \right\}}}\) and \(b_{\text{j}}^{{\left\{ {{\text{WGS}}84} \right\}}}\), with j = 1,…, 88, were measured with a differential GNSS receiver in the {WGS84} reference system. The multispectral imaging was done on the entire study site to provide a method to evaluate the LAI on extended vineyards by using remotely sensed data easily.

Point cloud processing algorithm for LAI estimation

This new typology of complex 3D representation of crop canopy can provide valuable information on the plant status. However, this huge amount of data cannot be generally used in raw form. Specific algorithms are required to extract relevant information to describe the cropland (e.g. introducing discrete parameters or indexes). The algorithm here presented was developed to extract information for LAI estimation in vineyards from 3D point clouds. To this extent, a set of canopy descriptors regarding the leaf density distribution along the canopy wall, the canopy thickness, and the canopy height were introduced and computed.

Point cloud processing

A 3D point cloud can be defined as a set of points

$${\mathcal{M}}^{{\left\{ {{\text{WGS}}84} \right\}}} = \left\{ {p_{\text{i}} = \left[ {{\upvarphi }_{\text{i}} ,{\uplambda }_{\text{i}} , e_{\text{i}} } \right]^{\text{T}} \in {\mathbb{R}}^{3} ;{\text{i}} = 1, \ldots ,{\text{card}}\left( {\mathcal{M}} \right)} \right\}$$
(1)

where \(\varphi_{\text{i}}\), \(\lambda_{\text{i}}\) and \(e_{\text{i}}\) are the latitude, longitude and elevation of each point \(p_{\text{i}}\) of the 3D model in the {WGS84} reference system.

The proposed 3D point cloud processing technique was defined by considering vineyard blocks (portions of vine row) of about 8 m length, which include few nearby vines. The vineyard block/section can be represented by a subset of points \({\mathcal{S}}_{\text{j}}\) (Fig. 1a, Supplementary Material 1), extracted from the 3D point cloud \({\mathcal{M}}^{{\left\{ {{\text{WGS}}84} \right\}}}\) in accordance with the position of two points \(a_{\text{j}}^{{\left\{ {{\text{WGS}}84} \right\}}}\) and \(b_{\text{j}}^{{\left\{ {{\text{WGS}}84} \right\}}}\), which are the GPS measured positions of two vines trellises (endpoints of the vineyard block). Subset \({\mathcal{S}}_{\text{j}}\) was then represented in a local Metrical Cartesian reference frame \(\left\{ {{\text{LOC}}_{\text{j}} } \right\}\), with the origin \(O_{{{\text{LOC}}_{\text{j}} }}^{{\left\{ {{\text{WGS}}84} \right\}}}\) located in \(a_{\text{j}}^{{\left\{ {{\text{WGS}}84} \right\}}}\) and with the \(x_{\text{j}}\) and \(z_{\text{j}}\) axes aligned with the wine row (segment \(\overline{{a_{\text{j}} b_{\text{j}} }}\)) and the vertical axis respectively (the \(y_{\text{j}}\) axis completes the Cartesian reference system). With this definition, subset \({\mathcal{S}}_{\text{j}}^{{\{ {\text{LOC}}_{\text{j}} \} }}\) is thus constituted only by points \(p_{\text{i}}\) as

$${\mathcal{S}}_{\text{j}}^{{\{ {\text{LOC}}_{\text{j}} \} }} = \left\{ {p_{\text{i}} = \left[ {x_{\text{i}} ,y_{\text{i}} ,z_{\text{i}} } \right]^{\text{T}} \in {\mathbb{R}}^{3} | 0 \le x_{\text{i}} \le b_{{{\text{j}},{\text{x}}}}^{{\{ {\text{LOC}}_{\text{j}} \} }} ,\left| {y_{\text{i}} } \right| \le \frac{{4\updelta_{\text{j}} }}{5} ; {\text{i}} = 1, \ldots ,{\text{card}}\left( {{\mathcal{S}}_{\text{j}} } \right)} \right\}$$
(2)

where \(b_{{{\text{j}},{\text{x}}}}^{{\{ {\text{LOC}}_{\text{j}} \} }}\) is the \(x\) coordinate of point \(b_{\text{j}}^{{\left\{ {{\text{WGS}}84} \right\}}}\) in the \(\left\{ {{\text{LOC}}_{\text{j}} } \right\}\) reference system and \({\updelta }_{\text{j}}\) is the local inter-row spacing distance, which can be automatically computed by using the methodology presented by Comba et al. (2018). Figure 1a (Supplementary Material 1) shows an sample vineyard block \({\mathcal{S}}_{52} ,\) represented in the local reference frame \(\left\{ {{\text{LOC}}_{52} } \right\}\) with origin in \(a_{52}^{{\left\{ {{\text{WGS}}84} \right\}}} = \left[ {44.62331, 7.99854, 365} \right]\).

Fig. 1
figure 1

a 3D point cloud model of subset \({\mathcal{S}}_{52}\) (green and brown dots). b Points of subsets \({\mathcal{A}}_{52}\) and \({\mathcal{B}}_{52}\) are highlighted in red and blue respectively. c Terrain model \({\upgamma}_{52}\) is blue coloured. d 3D point cloud model of subset \({\mathcal{R}}_{52}\) (green and brown dots) (Color figure online)

Full size image

To extract information from 3D point clouds, the selection of points representing the vine canopy and the knowledge of their height with respect to the terrain are a crucial issue. The reliability of the relative height (\(h_{\text{i}}\)) estimation of points \(p_{\text{i}} \subset {\mathcal{S}}_{\text{j}}\) is influenced by the accuracy of the terrain modelling, which can be particularly difficult when vineyards extend over hilly regions. Indeed, in the case of terracing, two adjacent inter-row paths can have different elevations. In the exemplificative vineyard block \({\mathcal{S}}_{52}\) in Fig. 1a (Supplementary Material 1), being extended over a sharply inclined sloping, the average elevation of the two inter-rows differs by about 0.4 m. The terrain of the two inter-row paths in \({\mathcal{S}}_{\text{j}}\) was therefore modelled by defining two subsets of points

$${\mathcal{A}}_{\text{j}} = \left\{ {p_{\text{i}} = \left[ {x_{\text{i}} ,y_{\text{i}} ,z_{\text{i}} } \right]^{\text{T}} \in {\mathcal{S}}_{\text{j}} | y_{\text{i}} + 0.25 \cdot \updelta < 0} \right\}$$
(3)

and

$${\mathcal{B}}_{\text{j}} = \left\{ {p_{\text{i}} = \left[ {x_{\text{i}} ,y_{\text{i}} ,z_{\text{i}} } \right]^{\text{T}} \in {\mathcal{S}}_{\text{j}} |y_{\text{i}} - 0.25 \cdot \updelta > 0} \right\},$$
(4)

which are highlighted in red and blue in Fig. 1b (Supplementary Material 1) respectively. Since vines are usually planted on the lower inter-row path, the relative height \(h_{\text{i}}\) of point \(p_{\text{i}} \subset {\mathcal{S}}_{\text{j}}\) was here calculated with respect to the terrain represented by the cluster having the lowest elevation between \({\mathcal{A}}_{\text{j}}\) and \({\mathcal{B}}_{\text{j}}\). The lowest elevation between \({\mathcal{A}}_{\text{j}}\) and \({\mathcal{B}}_{\text{j}}\) was determined by evaluating their centroids (arithmetic mean position of all the points). The terrain of subsets \({\mathcal{S}}_{\text{j}}\) having the lowest elevation was thus modelled by the plane

$$\gamma_{\text{j}} = \left\{ {\left[ {x,y,z} \right]^{\text{T}} \in {\mathbb{R}}^{3} { \sim }a_{{\gamma_{\text{j}} }} \left( {x - \bar{x}_{{{\mathcal{D}}_{\text{j}} }} } \right) + b_{{\gamma_{\text{j}} }} \left( {y - \bar{y}_{{{\mathcal{D}}_{\text{j}} }} } \right) + c_{{\gamma_{\text{j}} }} \left( {z - \bar{z}_{{{\mathcal{D}}_{\text{j}} }} } \right) = 0} \right\}$$
(5)

where \(\bar{x}_{{{\mathcal{D}}_{\text{j}} }}\), \(\bar{y}_{{{\mathcal{D}}_{\text{j}} }}\) and \(\bar{z}_{{{\mathcal{D}}_{\text{j}} }}\) are the centroid coordinates of \({\mathcal{D}}_{\text{j}}\), with \({\mathcal{D}}_{\text{j}}\) being the subset with the lowest centroid between \({\mathcal{A}}_{\text{j}}\) and \({\mathcal{B}}_{\text{j}}\). Coefficients \(a_{{\gamma_{\text{j}} }}\), \(b_{{\gamma_{\text{j}} }}\) and \(c_{{\gamma_{\text{j}} }}\) were obtained by solving the following optimisation problem

$$\mathop {\hbox{min} }\limits_{{{\text{a}}_{\text{j}} , {\text{b}}_{\text{j}} , {\text{c}}_{\text{j}} \in {\mathbb{R}}}} \mathop \sum \limits_{{{\text{i}} = 1}}^{{{\text{card}}\left( {{\mathcal{D}}_{\text{j}} } \right)}} \frac{{\left( {a_{\text{j}} \left( {x_{\text{i}} - \bar{x}_{{{\mathcal{D}}_{\text{j}} }} } \right) + b_{\text{j}} \left( {y_{\text{i}} - \bar{y}_{{{\mathcal{D}}_{\text{j}} }} } \right) + c_{\text{j}} \left( {z_{\text{i}} - \bar{z}_{{{\mathcal{D}}_{\text{j}} }} } \right)} \right)^{2} }}{{a_{\text{j}}^{2} + b_{\text{j}}^{2} + c_{\text{j}}^{2} }}$$
(6)

The relative height \(h_{\text{i}}\) of point \(p_{\text{i}} \subset {\mathcal{S}}_{\text{j}}\) was calculated with respect to plane \(\gamma_{\text{j}}\) as

$$h_{\text{i}} = z_{\text{i}} + c_{\text{j}}^{ - 1} \left( {a_{\text{j}} \left( {x_{\text{i}} - \bar{x}_{{{\mathcal{D}}_{\text{j}} }} } \right) + b_{\text{j}} \left( {y_{\text{i}} - \bar{y}_{{{\mathcal{D}}_{\text{j}} }} } \right)} \right) - \bar{z}_{{{\mathcal{D}}_{\text{j}} }} , \forall p_{\text{i}} \subset {\mathcal{S}}_{\text{j}}$$
(7)

thus obtaining a new 3D point cloud in the \(\left\{ {{\text{LOC}}_{\text{j}} } \right\}\) reference system as

$${\mathcal{R}}_{\text{j}} = \left\{ { q = \left[ {x, y, h} \right]^{\text{T}} \in {\mathbb{R}}^{3} : \forall p = \left[ {x, y, z} \right]^{\text{T}} \in {\mathcal{S}}_{\text{j}} } \right\}$$
(8)

An example of \({\mathcal{R}}_{\text{j}}\), obtained by subtracting the terrain model \({\upgamma }_{\text{j}}\) from subset \({\mathcal{S}}_{\text{j}}\), is shown in Fig. 1d. Finally, once the relative point height \(h_{\text{i}}\) with respect to the terrain was obtained by processing \({\mathcal{S}}_{\text{j}}\) (Eqs. 2–7), the procedure to select points representing only the canopy leads the following set

$${\mathcal{C}}_{\text{j}} = \left\{ { q_{\text{i}} = \left[ {x_{\text{i}} , y_{\text{i}} , h_{\text{i}} } \right]^{\text{T}} \in {\mathcal{R}}_{\text{j}} | \left| {y_{\text{i}} } \right| \le 0.8, h_{\text{i}} \ge 0.6} \right\}$$
(9)

which excludes \({\mathcal{R}}_{\text{j}}\) points with a height below 0.6 m with respect to the terrain. Indeed, excluded points mainly represent the trunk portion of vines without canopy.

The presented automatic procedures (Eqs. 2–9) allow only the points representing the vine canopy to be selected. This is crucial to avoid misleading and/or biased results from the following 3D point cloud processing steps, which focus on adequately extracting relevant information to formally describe the vineyard block under study by discrete parameters.

Canopy wall density distribution

An essential vine canopy descriptor for LAI evaluation is related to the spatial distribution of the leaves along the canopy wall. The aim is to represent, with a single numerical value, the complex canopy wall density distribution of the 3D point cloud \({\mathcal{C}}_{\text{j}}\). With the coordinates of subset \({\mathcal{C}}_{\text{j}}\) points within the ranges xmin ≤ x ≤ xmax, ymin ≤ y ≤ ymax and hmin ≤ h ≤ hmax, an analysis of the point density variability was conducted by defining a subset \({\mathcal{T}}_{{{\text{r}},{\text{s}}}}\), within a cuboid (rectangular prism) with height and width equal to \(\ell\), as follows:

$${\mathcal{T}}_{{{\text{r}},{\text{s}}}} \left( \ell \right) = \left\{ {q_{\text{i}} \in {\mathcal{C}}_{\text{j}} | \left( {r - 1} \right) \cdot \ell \le x_{\text{i}} < r \cdot \ell , \left( {s - 1} \right) \cdot \ell \le h_{\text{i}} - h_{ \text{min} } < s \cdot \ell } \right\}$$
(10)

with \({\text{r}} \in {\text{R}} = \left\{ {1,2, \ldots ,\frac{{x_{ \text{max} } - x_{ \text{min} } }}{\ell }} \right\}\) and \({\text{s}} \in {\text{S}} = \left\{ {1,2, \ldots ,\frac{{h_{ \text{max} } - h_{ \text{min} } }}{\ell }} \right\}\). An example of subset \({\mathcal{T}}_{{{\text{r}},{\text{s}}}}\), obtained by processing section \({\mathcal{C}}_{\text{j}}\) with \(\ell\) equal to 0.2 m, is highlighted in red in Fig. 2a (Supplementary Material 2). Indeed, by considering the number of points of subset \({\mathcal{T}}_{{{\text{r}},{\text{s}}}} \left( \ell \right)\), a 2D map \({\mathcal{N}}_{\text{j}}\) can be derived as

Fig. 2
figure 2

a Portion of point cloud \({\mathcal{R}}_{52}^{{\left\{ {{\text{Loc}}_{52} } \right\}_{{}} }}\) and subset \({\mathcal{C}}_{52}\) (green dots). Points of the subset \({\mathcal{T}}_{35,4} \left( \ell \right)\), with \(\ell = 0.2\) m, are highlighted in red. Values of matrix \({\mathcal{N}}_{52}\) are graphically represented in the background (images on the x–h plane), properly aligned with x and h coordinates used to compute \(n_{{{\text{r}},{\text{s}}}}\) values. b Enlargement of a portion of (a), with \({\mathcal{T}}_{35,4}\). The colour bar is related to the colour scale adopted to represent matrix \({\mathcal{N}}_{52}\) (Color figure online)

Full size image
$${\mathcal{N}}_{\text{j}} = \left\{ {n_{{{\text{r}},{\text{s}}}} = {\text{card}}\left( {{\mathcal{T}}_{{{\text{r}},{\text{s}}}} } \right) \cdot \ell^{ - 2} \forall r \in {\text{R}},s \in {\text{S}}} \right\}$$
(11)

which represents the density distribution of the \({\mathcal{C}}_{\text{j}}\) points along the plane x–h. As an example, matrix \({\mathcal{N}}_{\text{j}}\) computed with r ∈ {1, 2,…, 42} and s ∈ {1, 2,…, 7} is graphically represented in Fig. 2a (Supplementary Material 2).

The obtained matrix \({\mathcal{N}}_{\text{j}}\) is affected by the parameter \(\ell\) value, which is related to the specific degree of detail of the 2D canopy density distribution map. Indeed, small values of \(\ell\) could lead to matrix \({\mathcal{N}}_{\text{j}}\) better describing the canopy density inhomogeneities. However, a too small value of \(\ell\) could generate a matrix \({\mathcal{N}}_{\text{j}}\) with empty elements, thus limiting the canopy wall map effectiveness. Several metrics can be defined to properly describe values of matrix \({\mathcal{N}}_{\text{j}}\). The descriptor \(d_{{{\text{x}},{\text{j}}}}\) was here defined as the ratio between the amount of elements greater than \(t_{\text{w}}\) and the overall two-dimensional map size, as

$$d_{{{\text{x}},{\text{j}}}} \left( \ell \right) = \frac{{\mathop \sum \nolimits_{{{\text{r}} = 1}}^{\left\lceil{{\frac{{x_{ \text{max} } - x_{ \text{min} } }}{\ell }}}\right\rceil} \mathop \sum \nolimits_{{{\text{s}} = 1}}^{\left\lceil{{\frac{{h_{ \text{max} } - h_{ \text{min} } }}{\ell }}}\right\rceil} g\left( {n_{{{\text{r}},{\text{s}}}} } \right)}}{{{\left\lceil\frac{{x_{ \text{max} } - x_{ \text{min} } }}{\ell }\right\rceil} \cdot {\left\lceil\frac{{h_{ \text{max} } - h_{ \text{min} } }}{\ell }\right\rceil}}}$$
(12)

where function \(g\left( {n_{{{\text{r}},{\text{s}}}} } \right)\) is equal to 0 if \(n_{{{\text{r}},{\text{s}}}} < t_{\text{w}}\) and to 1 otherwise. The selected value of \(t_{\text{w}}\) was \(0.2 \cdot w_{{\mathcal{N}}}\), with \(w_{{\mathcal{N}}}\) being the average point cloud density.

Canopy thickness

Vine canopy thickness is one of the key parameters necessary to properly evaluate the LAI. The analysis was performed by considering only the points representing crop canopy, collected in subset \({\mathcal{C}}_{\text{j}}\). A projection on the y–z plane of points of subset \({\mathcal{C}}_{52}\) is shown in Fig. 3 (Supplementary Material 3). To find reliable crop canopy thickness descriptors, several metrics of the \(y\) coordinates distribution of points of subsets \({\mathcal{C}}_{\text{j}}\) were considered. The evaluated canopy thickness-based descriptors include difference \(d_{{{\text{y}}_{\text{I}} , {\text{j}}}} = y_{ \text{max} } - y_{ \text{min} }\) and specific differences between percentile pairs, such as \(d_{{{\text{y}}_{\text{II}} , {\text{j}}}} = P_{98} - P_{2}\) between the 98th and 2nd percentiles of the \(y\) coordinates.

Fig. 3
figure 3

a Point cloud subset \({\mathcal{R}}_{52}\) (green and brown dots) together with the projection of canopy points (\({\mathcal{C}}_{52}\)) on the y–h plane (red dots). b Enlargement of canopy points (\({\mathcal{C}}_{52}\)) projection and boxplots (Color figure online)

Full size image

Canopy height

The approach used to describe the canopy thickness was adopted to extract information from the 3D point cloud regarding the vine canopy height. Therefore, several metrics of the \(h\) coordinates distribution of canopy points \({\mathcal{C}}_{\text{j}}\) were considered to find reliable descriptors representing the canopy height. The evaluated canopy height-based descriptors include the \(h\) coordinate of the highest point \(d_{{{\text{z}}_{\text{I}} , {\text{j}}}} = \hbox{max} \left( {h_{\text{i}} } \right)\) and the 70th, 80th, 90th and 95th percentiles.

LAI modelling framework

Several published research papers have demonstrated a linear relationship between crop LAI and several crop biophysical measurements and/or remotely sensed datasets, such as fresh and dry biomass in wheat production (Schirrmann et al. 2015) or Normalised Difference Vegetation Index (Johnson et al. 2003). Valuable contributions have also been derived from Córcoles et al. (2013), who found a linear model to be significant in correlating LAI and canopy cover, and from Mathews and Jensen (2013), who proved the reliability of linear modelling in describing LAI with canopy height-based metrics. In accordance with these results in the literature, the relationship between the defined crop canopy descriptors and the LAI was here modelled by a multivariate linear model as

$${\text{LAI}}_{\text{j}} = \left( {\mathop \sum \limits_{{{\text{k }} \in D}} c_{\text{k}} \cdot d_{{{\text{k}},{\text{j}}}} + {\text{q}}} \right) \cdot \updelta_{\text{j}}^{ - 1}$$
(13)

where \(D\) is the set of selected descriptors \(d_{\text{k}}\), \(c_{\text{k}}\) is the coefficient of descriptor \(d_{\text{k}}\), \({\text{q}}\) is the model intercept and \(\updelta_{\text{j}}\) is the vineyard inter-row spacing. By means of a stepwise multilinear least-squares optimisation approach (Lawson and Hanson 1974), the in-field data were used to select the most reliable crop descriptors. The generalised extreme Studentised deviate test was used to remove outliers from the dataset of descriptors and the robustness of the obtained model in LAI estimation was tested using the leave-one-out exhaustive cross-validation.

Results and discussion

The obtained solution for estimating \({\text{LAI}}_{\text{j}}^{ *}\), investigated by using a stepwise multilinear least-squares problem solver approach (Statistics and Machine Learning Toolbox™, Matlab), was the three-variable linear model

$${\text{LAI}}_{\text{j}}^{ *} = \left( {0.12 \cdot d_{{x_{\text{IV}} ,{\text{j}}}} + 0.39 \cdot d_{{{\text{y}}_{\text{II}} ,{\text{j}}}} + 1.00 \cdot d_{{{\text{z}}_{\text{IV}} ,{\text{j}}}} - 0.87} \right) \cdot \updelta_{\text{j}}^{ - 1}$$
(14)

with \(d_{{{\text{x}}_{\text{IV}} }}\), \(d_{{{\text{y}}_{\text{II}} }}\) and \(d_{{{\text{z}}_{\text{IV}} }}\) being the most effective descriptors of the canopy among defined ones (Table 2) and \(\updelta_{\text{j}}\) the inter-row spacing. In the considered experimental site \(\updelta_{\text{j}}\) differs slightly among different vineyard blocks, ranging between 2.3 and 2.4 m. In particular, a set of 15 descriptors was computed for all the subsets \({\mathcal{C}}_{\text{j}}\), with j = 1,…, 88: six descriptors related to the canopy wall density distribution (from \(d_{{{\text{x}}_{\text{I}} }}\) to \(d_{{{\text{x}}_{\text{VI}} }}\)) for the \(\ell\) parameter ranging from 0.05 to 0.30 m, four descriptors related to the canopy thickness (from \(d_{{{\text{y}}_{\text{I}} }}\) to \(d_{{{\text{y}}_{\text{IV}} }}\)) and five to the canopy height (from \(d_{{z_{\text{I}} }}\) to \(d_{{{\text{z}}_{\text{V}} }}\)). An example of the computed descriptors of subset \({\mathcal{C}}_{52}\) is reported in Table 2.

Table 2 Descriptors set definitions and computed values processing the sample subset \({\mathcal{C}}_{52}\)
Full size table

The vineyard LAI estimated from dense 3D point clouds by the proposed methodology (Eq. 14) showed to be well correlated with ones obtained by the traditional manual method of the inclined point quadrat. The obtained R2 value of 0.82 can be considered fully positive, being largely greater than 0.5. Indeed, 0.5 is the value indicated in several research works (Ricci et al. 2019; Sun et al. 2018) as the threshold in considering a good correlation between the estimated and measured LAI. Please note that this value takes into account the accuracy of the reference LAI manual measurement (Wilson 1963). In Fig. 4a, estimated \({\text{LAI}}_{\text{j}}^{ *}\) values are plotted in relation to the in-field LAI ones while in Fig. 4b LAI values are plotted in relation to the principal component PCA1 of the selected descriptors space \(\left[ { d_{{{\text{x}}_{\text{IV}} }} , d_{{{\text{y}}_{\text{II}} }} ,d_{{{\text{z}}_{\text{IV}} }} } \right]\).

Fig. 4
figure 4

a Scatterplot of \({\text{LAI}}_{{}}^{ *}\) estimated values by the proposed method and in-field measured LAI. b Visualisation of the model output as a function of the principal component PCA1 of the descriptors space \(\left[ { d_{{{\text{x}}_{\text{IV}} }} , d_{{{\text{y}}_{\text{II}} }} ,d_{{{\text{z}}_{\text{IV}} }} } \right]\)

Full size image

In addition, the robustness of the proposed modelling approach for LAI estimation was investigated with the leave-one-out cross-validation (LOOCV) method. This verification makes it possible to evaluate the model performance in estimating an LAI value without using it in the model calibration. Two error indices commonly used in LOOCV were computed (Consonni et al. 2009; Richardson and Reeves 2005): (1) the cross-validated coefficient of determination (Q2) and (2) the standard error of cross-validation (SECV), defined as

$${\text{Q}}^{2} = 1 - \frac{{\mathop \sum \nolimits_{{{\text{i}} = 1}}^{{N_{\text{b}} }} \left( {{\text{LAI}}_{\text{i}}^{{ *\left( { - {\text{i}}} \right)}} - {\text{LAI}}_{\text{i}} } \right)^{2} }}{{\mathop \sum \nolimits_{{{\text{i}} = 1}}^{{N_{\text{b}} }} \left( {\overline{\text{LAI}}^{{\left( { - {\text{i}}} \right)}} - {\text{LAI}}_{\text{i}} } \right)^{2} }}$$
(15)

and

$${\text{SECV}} = \frac{1}{{N_{\text{b}} }}\mathop \sum \limits_{{{\text{i}} = 1}}^{{N_{\text{b}} }} \left( {{\text{LAI}}_{\text{i}}^{{ *\left( { - {\text{i}}} \right)}} - {\text{LAI}}_{\text{i}} } \right)^{2}$$
(16)

where \(N_{\text{b}} = 87\) is the number of considered vineyard blocks, \(\overline{\text{LAI}}^{{\left( { - {\text{i}}} \right)}}\) is the in-field LAI assessments average, excluding the \({\text{i}}\)-th one, and \({\text{LAI}}_{\text{i}}^{{ *\left( { - {\text{i}}} \right)}}\) is the evaluated LAI by the model fitting descriptors \(d_{{{\text{k}},{\text{j}}}}\), with \({\text{j}} = 1, \ldots , {\text{N}}_{\text{b}}\), \({\text{j}} \ne {\text{i}}\) and \({\text{k}} \in \left\{ {{\text{x}}_{\text{IV}}, {\text{y}}_{\text{II}}, {\text{z}}_{\text{IV}} } \right\}\). The obtained Q2 and SECV values, which are 0.80 and 0.029 respectively, confirmed the goodness of the obtained model for estimating the LAI. Indeed, considering the same application, the values of Q2, which are considered positive correlation indicators, are equal to the ones determined for R2. In this specific application, values higher than 0.5 are fully satisfactory (Ricci et al. 2019; Sun et al. 2018). Concerning the SECV, values lower than 5% can be considered well within the error limits to obtain a robust model (Richardson and Reeves 2005).

Conclusions

Overall, this study showed that the estimation of LAI by processing dense 3D point clouds offers a viable and cost-effective alternative to traditional LAI assessments. This allows for high resolution, extensive and fast mapping of the index, even in hilly and not easily accessible regions. The LAI was estimated by a multivariate linear regression model on a subset of 15 crop canopy descriptors, which account for the canopy thickness, height and leaf density distribution along the wall. These crop canopy descriptors were computed by developing new specific 3D point cloud processing algorithms.

For the validation of the estimated LAI, an experiment was conducted in three vineyard plots in Serralunga d’Alba (Italy). The leaf area of more than 700 vines was manually measured by the inclined point quadrant approach and six UAV flights were contextually performed to acquire aerial images of the whole vineyard. The vineyard LAI estimated by the proposed methodology showed to be correlated with the ones obtained by the traditional manual method. Indeed, the obtained R2 value of 0.82 can be considered fully adequate, compatible to the accuracy of the reference LAI manual measurement. Data acquisition, performed at six different vine phenological phases, made the developed method reliable to estimate the LAI during the whole growing cycle.

The proposed methodology allows for rapid, cost effective and extensive evaluation of the LAI in large vineyards with a degree of detail comparable to the typical in-field operations of precision viticulture. It overcomes the limits of traditional LAI assessment methods, which are generally laborious and provide information within limited areas. The flexibility of UAV platforms can be used to estimate the LAI at the required time and growing periods, overcoming satellite imaging schedules. By combining the results of this work with the ones provided by Comba et al. (2018), the LAI can be rapidly evaluated by a generic 3D point cloud of croplands, in a completely automatic manner, without any user intervention or manual vineyard boundary selection.