A Geographically Temporal Weighted Regression Approach with Travel Distance for House Price Estimation
Abstract
:1. Introduction
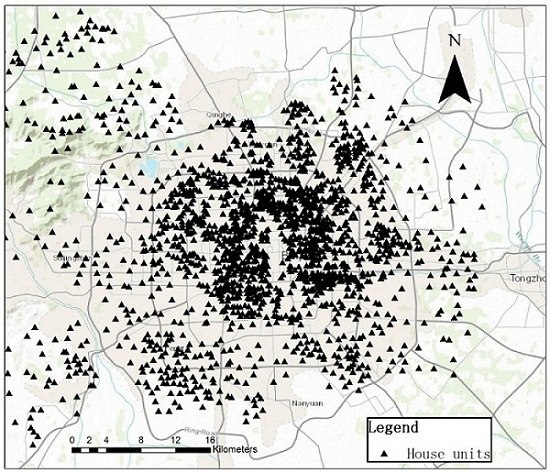
2. Study Area and Experimental Data
3. Methods
3.1. Geographically Temporal Weighted Regression Model
3.2. Measuring Travel Distance on a Beijing Road Network
3.3. The Proposed Algorithm Flow
4. Experimental Results and Comparisons
4.1. Spatial and Temporal Heterogeneity Test of Significance
4.2. Comparison of the GTWR and GWR Models with Euclidean and Travel Distance Metrics
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Tobler, W.R. A computer movie simulating urban growth in the Detroit region. Econ. Geogr. 1970, 46, 234–240. [Google Scholar] [CrossRef]
- Griffith, D.A. Spatial-filtering based contributions to a critique of geographically weighted regression (GWR). Environ. Plan. A 2008, 40, 2751–2769. [Google Scholar] [CrossRef]
- Brunsdon, C.; Fotheringham, A.S.; Charlton, M.E. Geographically weighted regression: A method for exploring spatial nonstationarity. Geogr. Anal. 1996, 28, 281–298. [Google Scholar] [CrossRef]
- Farber, S.; Páez, A. A systematic investigation of cross-validation in GWR model estimation: Empirical analysis and Monte Carlo simulations. J. Geogr. Syst. 2007, 9, 371–396. [Google Scholar] [CrossRef]
- Bitter, C.; Mulligan, G.F.; Dallérba, S. Incorporating spatial variation in housing attribute prices: A comparison of geographically weighted regression and the spatial expansion method. J. Geogr. Syst. 2007, 9, 7–27. [Google Scholar] [CrossRef] [Green Version]
- Wei, C.H.; Qi, F. On the estimation and testing of mixed geographically weighted regression models. Econ. Modell. 2012, 29, 2615–2620. [Google Scholar] [CrossRef]
- Helbich, M.; Brunauer, W.; Vaz, E.; Nijkamp, P. Spatial heterogeneity in hedonic house price models: The case of Austria. Urban Stud. 2014, 51, 390–411. [Google Scholar] [CrossRef]
- Lu, B.; Charlton, M.; Fotheringhama, A.S. Geographically weighted regression using a non-euclidean distance metric with a study on London house price data. Procedia Environ. Sci. 2011, 7, 92–97. [Google Scholar] [CrossRef]
- Lu, B.; Charlton, M.; Harris, P.; Fotheringham, A.S. Geographically weighted regression with a non-euclidean distance metric: A case study using hedonic house price data. Int. J. Geogr. Inf. Sci. 2014, 28, 660–681. [Google Scholar] [CrossRef]
- Mcmillen, D.P.; Redfearn, C.L. Estimation, Interpretation, and Hypothesis Testing for Nonparametric Hedonic House Price Functions. Available online: http://lusk.usc.edu/sites/default/files/working_papers/wp_2007-1007.pdf (accessed on 11 August 2016).
- Mcmillen, D.P.; Redfearn, C.L. Estimation and hypothesis testing for nonparametric hedonic house price functions. J. Reg. Sci. 2010, 50, 712–733. [Google Scholar] [CrossRef]
- Bai, Y.; Wu, L.; Qin, K.; Zhang, Y.; Shen, Y.; Zhou, Y. A geographically and temporally weighted regression model for ground-level PM2.5 estimation from satellite-derived 500 m resolution AOD. Remote Sens. 2016, 8, 262. [Google Scholar] [CrossRef]
- Huang, B.; Wu, B.; Barry, M. Geographically and temporally weighted regression for modeling spatio-temporal variation in house prices. Int. J. Geogr. Inf. Sci. 2010, 24, 383–401. [Google Scholar] [CrossRef]
- Wrenn, D.H.; Sam, A.G. Geographically and temporally weighted likelihood regression: Exploring the spatiotemporal determinants of land use change. Reg. Sci. Urban Econ. 2014, 44, 60–74. [Google Scholar] [CrossRef]
- Griffith, D.A. Spatial Autocorrelation: A Primer; Assn of Amer Geographers: Washington, DC, USA, 1987. [Google Scholar]
- Wu, B.; Li, R.; Huang, B. A geographically and temporally weighted autoregressive model with application to housing prices. Int. J. Geogr. Inf. Sci. 2014, 28, 1186–1204. [Google Scholar] [CrossRef]
- Ahlfeldt, G. If Alonso was right: Modeling accessibility and explaining the residential land gradient. J. Reg. Sci. 2011, 51, 318–338. [Google Scholar] [CrossRef]
- Apparicio, P.; Abdelmajid, M.; Riva, M.; Shearmur, R. Comparing alternative approaches to measuring the geographical accessibility of urban health services: Distance types and aggregation-error issues. Int J. Health Geogr. 2008, 7. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mcgrail, M.R.; Humphreys, J.S. Measuring spatial accessibility to primary care in rural areas: Improving the effectiveness of the two-step floating catchment area method. Appl. Geogr. 2009, 29, 533–541. [Google Scholar] [CrossRef]
- Schuurman, N.; Bérubé, M.; Crooks, V.A. Measuring potential spatial access to primary health care physicians using a modified gravity model. Can. Geogr. 2010, 54, 29–45. [Google Scholar] [CrossRef]
- Yiannakoulias, N.; Bland, W.; Svenson, L.W. Estimating the effect of turn penalties and traffic congestion on measuring spatial accessibility to primary health care. Appl. Geogr. 2013, 39, 172–182. [Google Scholar] [CrossRef]
- Lu, B.; Charlton, M.; Brunsdon, C. The Minkowski approach for choosing the distance metric in geographically weighted regression. Int. J. Geogr. Inf. Sci. 2015, 30, 351–368. [Google Scholar] [CrossRef]
- Selim, H. Determinants of house prices in Turkey: Hedonic regression versus artificial neural network. Expert Syst. Appl. 2009, 36, 2843–2852. [Google Scholar] [CrossRef]
- Redfearn, C.L. How informative are average effects? Hedonic regression and amenity capitalization in complex urban housing markets. Reg. Sci. Urban Econ. 2009, 39, 297–306. [Google Scholar] [CrossRef]
- Peterson, S.; Flanagan, A. Neural network hedonic pricing models in mass real estate appraisal. J. R. Estate Res. 2009, 31, 147–164. [Google Scholar]
- Paez, A.; Long, F.; Farber, S. Moving window approaches for hedonic price estimation: An empirical comparison of modelling techniques. Urban Stud. 2008, 45, 1565–1581. [Google Scholar] [CrossRef]
- Farber, S.; Yeates, M. A comparison of localized regression models in a hedonic house price context. Can. J. Reg. Sci. 2006, 29, 405–420. [Google Scholar]
- Selim, S. Determinants of house prices in turkey: A hedonic regression model. Doğuş Üniversitesi Dergisi 2008, 9, 65–76. [Google Scholar]
- Guan, J.; Zurada, J.; Levitan, A. An adaptive neuro-fuzzy inference system based approach to real estate property assessment. J. R. Estate Res. 2008, 30, 395–422. [Google Scholar]
- Kuşan, H.; Aytekin, O.; Özdemir, İ. The use of fuzzy logic in predicting house selling price. Expert Syst. Appl. 2010, 37, 1808–1813. [Google Scholar] [CrossRef]
- Barr, J.; Cohen, J.P. The floor area ratio gradient: New York City, 1890–2009. Reg. Sci. Urban Econ. 2014, 48, 110–119. [Google Scholar] [CrossRef]
- Garcia, C.B.; Garcia, J.; Martin, M. Collinearity: Revisiting the variance inflation factor in ridge regression. J. Appl. Stat. 2015, 42, 648–661. [Google Scholar] [CrossRef]
- Wheeler, D.; Tiefelsdorf, M. Multicollinearity and correlation among local regression coefficients in geographically weighted regression. J. Geogr. Syst. 2005, 7, 161–187. [Google Scholar] [CrossRef]
- Wheeler, D.C. Diagnostic tools and a remedial method for collinearity in geographically weighted regression. Environ. Plan. A 2007, 39, 2464–2481. [Google Scholar] [CrossRef]
- Páez, A.; Farber, S.; Wheeler, D. A simulation-based study of geographically weighted regression as a method for investigating spatially varying relationships. Environ. Plan. A 2011, 43, 2992–3010. [Google Scholar] [CrossRef]
- Cho, S.; Lambert, D.M.; Kim, S.G.; Jung, S. Extreme coefficients in geographically weighted regression and their effects on mapping. GIsci. Remote Sens. 2009, 46, 273–288. [Google Scholar] [CrossRef]
- Harris, R.; Dong, G.; Zhang, W. Using contextualized geographically weighted regression to model the spatial heterogeneity of land prices in Beijing, China. Trans. GIS 2013, 17, 901–919. [Google Scholar] [CrossRef]
- Curriero, F.C. On the use of non-euclidean distance measures in geostatistics. Math. Geol. 2007, 38, 907–926. [Google Scholar] [CrossRef]
- Leung, Y.; Mei, C.; Zhang, W. Statistical tests for spatial nonstationarity based on the geographically weighted regression model. Environ. Plan. A 2000, 32, 9–32. [Google Scholar] [CrossRef]
- Fotheringham, A.S.; Brunsdon, C.; Charlton, M. Geographically weighted regression: The analysis of spatially varying relationships. Am. J. Agric. Econ. 2004, 86, 554–556. [Google Scholar]



| Abbreviation | Description | Minimum | Mean | Maximum |
|---|---|---|---|---|
| LnPrice | Log of the sales transaction price of the house | 3.807 | 6.071 | 10.309 |
| Structural Covariates | ||||
| LnPlotRatio | Log of the plot ratio of houses | −4.605 | 0.679 | 2.303 |
| LnGreenRatio | Log of the green ratio | −5.809 | −1.162 | −0.116 |
| LnFloorArea | Log of the total floor area | 2.303 | 4.532 | 7.507 |
| LnPropertyFee | Log of the property management fee | −0.693 | 0.346 | 4.060 |
| Temporal Covariates | ||||
| Age | Age of the building at the time of sale (1980–2015) | 1 | 23 | 30 |
| Neighborhood Covariates | ||||
| Log of the Euclidean distance to the nearest primary school | 0.499 | 6.393 | 16.322 | |
| Log of the Euclidean distance to the nearest shopping mall | 2.153 | 5.752 | 16.342 | |
| Log of the travel distance to the nearest primary school | 1.386 | 6.462 | 12.701 | |
| Log of the travel distance to the nearest shopping mall | 1.946 | 6.203 | 12.738 |
| Parameter | Euclidean Distance | Travel Distance | ||
|---|---|---|---|---|
| F value | p-value | F value | p-value | |
| Intercept | 6.398 | <0.001 * | 9.858 | <0.001 * |
| LnPlotRatio | 1.140 | 0.178 | 1.718 | <0.001 * |
| LnGreenRatio | 5.032 | <0.001 * | 7.772 | <0.001 * |
| LnFloorArea | 1.551 | <0.001 * | 2.619 | <0.001 * |
| LnPropertyFee | 1.040 | 0.389 | 1.542 | 0.083 |
| 1.453 | 0.012 * | 1.485 | <0.001 * | |
| 1.132 | 0.190 | 1.771 | <0.001 * | |
| Age | 1.435 | 0.007 * | 2.477 | <0.001 * |
| Parameter | Euclidean Distance | Travel Distance | ||
|---|---|---|---|---|
| F value | p-value | F value | p-value | |
| Intercept | 5.686 | <0.001 * | 3.275 | <0.001 * |
| LnPlotRatio | 2.844 | <0.001 * | 3.166 | <0.001 * |
| LnGreenRatio | 1.899 | <0.001 * | 3.057 | <0.001 * |
| LnFloorArea | 4.111 | <0.001 * | 2.653 | <0.001 * |
| LnPropertyFee | 1.864 | 0.065 | 2.283 | 0.004 * |
| 1.910 | <0.001 * | 2.246 | <0.001 * | |
| 3.103 | <0.001 * | 2.822 | <0.001 * | |
| Age | 12.882 | <0.001 * | 10.490 | <0.001 * |
| Parameter | Min | LQ | Med | UQ | Max |
|---|---|---|---|---|---|
| Intercept | −12.158 | 0.055 | 1.237 | 2.327 | 15.63 |
| LnPlotRatio | −1.209 | −0.056 | −0.004 | 0.047 | 1.607 |
| LnGreenRatio | −14.58 | −0.282 | 0.223 | 0.838 | 8.08 |
| LnFloorArea | 0.161 | 0.833 | 0.979 | 1.126 | 2.013 |
| LnPropertyFee | −7.734 | −0.104 | 1.9549 | 0.128 | 30.79 |
| −0.889 | −0.512 | −0.401 | −0.165 | −0.015 | |
| −1.294 | −0.055 | 0.013 | 0.088 | 0.802 | |
| Age | −0.42 | −0.006 | 0.01 | 0.028 | 0.37 |
| Parameter | Min | LQ | Med | UQ | Max |
|---|---|---|---|---|---|
| Intercept | −9.535 | 0.023 | 1.221 | 2.348 | 15.074 |
| LnPlotRatio | −0.58 | −0.054 | −0.003 | 0.047 | 0.913 |
| LnGreenRatio | −6.675 | −0.291 | 0.251 | 0.877 | 6.332 |
| LnFloorArea | 0.161 | 0.834 | 0.98 | 1.127 | 1.958 |
| LnPropertyFee | −6.542 | −0.104 | 1.085 | 0.132 | 21.21 |
| −0.892 | −0.554 | −0.410 | −0.218 | −0.018 | |
| −0.753 | −0.062 | 0.01 | 0.093 | 0.875 | |
| Age | −0.32 | −0.006 | 0.009 | 0.026 | 0.236 |
| Parameter | Min | LQ | Med | UQ | Max |
|---|---|---|---|---|---|
| Intercept | −5.04 | 0.376 | 1.283 | 2.172 | 7.249 |
| LnPlotRatio | −0.291 | −0.04 | −0.001 | 0.037 | 0.595 |
| LnGreenRatio | −3.422 | −0.194 | 0.201 | 0.594 | 4.162 |
| LnFloorArea | 0.161 | 0.883 | 1.004 | 1.134 | 1.546 |
| LnPropertyFee | −2.131 | −0.075 | 0.031 | 0.144 | 7.056 |
| −1.095 | −0.711 | −0.561 | −0.292 | −0.012 | |
| −1.2 | −0.038 | 0.013 | 0.068 | 0.454 | |
| Age | −0.091 | −0.002 | 0.005 | 0.014 | 0.107 |
| Parameter | Min | LQ | Med | UQ | Max |
|---|---|---|---|---|---|
| Intercept | −3.468 | 0.331 | 1.261 | 2.134 | 7.983 |
| LnPlotRatio | −0.262 | −0.039 | −0.002 | 0.035 | 0.588 |
| LnGreenRatio | −3.394 | −0.169 | 0.215 | 0.636 | 3.737 |
| LnFloorArea | 0.161 | 0.886 | 1.005 | 1.138 | 1.59 |
| LnPropertyFee | −2.238 | −0.07 | 0.032 | 0.141 | 7.309 |
| −1.182 | −0.644 | −0.412 | −0.258 | −0.005 | |
| −1.009 | −0.039 | 0.013 | 0.066 | 0.447 | |
| Age | −0.083 | −0.002 | 0.005 | 0.014 | 0.116 |
| Models | RSS | DF | MS | F-test | p-value | R2 | AIC |
|---|---|---|---|---|---|---|---|
| OLS | 465.0 | 8 | 58.12 | - | - | ||
| GWR(ED) | 278.6 | 1787.5 | 0.16 | 1.9 | 0 | 0.724 | 1750.305 |
| GWR(TD) | 265.2 | 1778.3 | 0.15 | 2.2 | 0 | 0.737 | 1659.183 |
| GTWR(ED) | 243.2 | 1768.9 | 0.14 | 2.3 | 0 | 0.759 | 1483.361 |
| GTWR(TD) | 218.8 | 1755.6 | 0.13 | 2.9 | 0 | 0.783 | 1276.761 |
| GWR(TD)/GWR(ED) Improvement | 13.4 | 9.2 | 1.46 | - | - | 0.013 | 91.122 |
| GTWR(TD)/GTWR(ED) Improvement | 24.3 | 13.3 | 1.83 | - | - | 0.024 | 206.6 |
| GTWR(TD)/GWR(TD) Improvement | 46.3 | 22.7 | 2.04 | - | - | 0.046 | 382.422 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Yang, Y.; Xu, S.; Zhao, Y.; Wang, Y.; Zhang, F. A Geographically Temporal Weighted Regression Approach with Travel Distance for House Price Estimation. Entropy 2016, 18, 303. https://doi.org/10.3390/e18080303
Liu J, Yang Y, Xu S, Zhao Y, Wang Y, Zhang F. A Geographically Temporal Weighted Regression Approach with Travel Distance for House Price Estimation. Entropy. 2016; 18(8):303. https://doi.org/10.3390/e18080303
Chicago/Turabian StyleLiu, Jiping, Yi Yang, Shenghua Xu, Yangyang Zhao, Yong Wang, and Fuhao Zhang. 2016. "A Geographically Temporal Weighted Regression Approach with Travel Distance for House Price Estimation" Entropy 18, no. 8: 303. https://doi.org/10.3390/e18080303
APA StyleLiu, J., Yang, Y., Xu, S., Zhao, Y., Wang, Y., & Zhang, F. (2016). A Geographically Temporal Weighted Regression Approach with Travel Distance for House Price Estimation. Entropy, 18(8), 303. https://doi.org/10.3390/e18080303