Multi-Sensor SAR Image Registration Based on Object Shape
Abstract
:1. Introduction
2. Methodology
2.1. Matching Primitives and Process
2.1.1. Matching Primitives
2.1.2. Registration Process
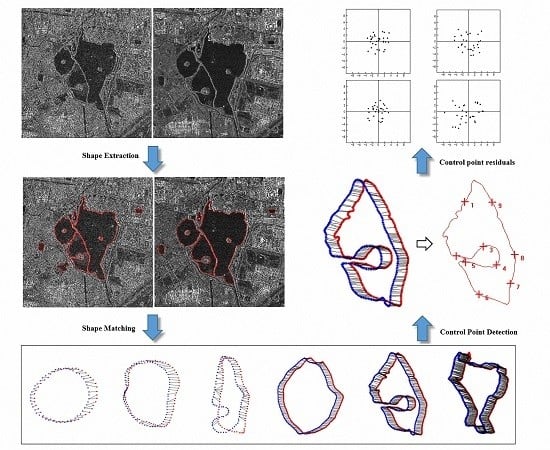
2.2. Shape Matching Using Shape Context
3. Experiment Results
3.1. Data Introduction
3.2. Shape Extraction and Shape Matching
3.3. Geometric Transformation and Registration Result
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Zitova, B.; Flusser, J. Image registration methods: A survey. Image Vis. Comput. 2003, 21, 977–1000. [Google Scholar] [CrossRef]
- Dawn, S.; Saxena, V.; Sharma, B. Remote sensing image registration techniques: A survey. In Proceedings of 4th International Conference on Image and Signal Processing (ICISP), Trois-Rivières, QC, Canada, 30 June–2 July 2010; Volume 6134, pp. 103–112.
- Gong, M.; Zhao, S.; Jiao, L.; Tian, D.; Wang, S. A novel coarse-to-fine scheme for automatic image registration based on SIFT and mutual information. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4328–4338. [Google Scholar] [CrossRef]
- Chen, T.; Chen, L. A union matching method for SAR images based on SIFT and edge strength. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 1–10. [Google Scholar]
- Zhu, H.; Ma, W.; Hou, B.; Jiao, L. SAR image registration based on multifeature detection and arborescence network matching. IEEE Geosci. Remote Sens. 2016, 13, 706–710. [Google Scholar] [CrossRef]
- Liang, J.; Liu, X.; Huang, K.; Li, X.; Wang, D.; Wang, X. Automatic registration of multisensor images using an integrated spatial and mutual information (SMI) metric. IEEE Trans. Geosci. Remote Sens. 2014, 52, 603–615. [Google Scholar] [CrossRef]
- Liu, F.; Bi, F.; Chen, L.; Shi, H.; Liu, W. Feature-Area optimization: A novel SAR image registration method. IEEE Geosci. Remote Sens. 2016, 13, 242–246. [Google Scholar] [CrossRef]
- Wang, B.; Zhang, J.; Lu, L.; Huang, G.; Zhao, Z. A uniform SIFT-like algorithm for SAR image registration. IEEE Geosci. Remote Sens. 2015, 12, 1426–1430. [Google Scholar] [CrossRef]
- Dellinger, F.; Delon, J.; Gousseau, Y.; Michel, J.; Tupin, F. SAR-SIFT: A SIFT-like algorithm for SAR images. IEEE Trans. Geosci. Remote Sens. 2015, 53, 453–466. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.; Ni, W.; Yan, W.; Wu, J.; Li, S. Robust SAR image registration based on edge matching and refined coherent point drift. IEEE Geosci. Remote Sens. 2015, 12, 1–5. [Google Scholar] [CrossRef]
- Li, H.; Manjunath, B.S.; Mitra, S.K. A contour-based approach to multisensor image registration. IEEE Trans. Image Process. 1995, 4, 320–334. [Google Scholar] [CrossRef]
- Eugenio, F.; Marques, F. Automatic satellite image georeferencing using a contour-matching approach. IEEE Trans. Geosci. Remote Sens. 2003, 41, 2869–2880. [Google Scholar] [CrossRef]
- Pan, C.; Zhang, Z.; Yan, H.; Wu, G.; Ma, S. Multisource data registration based on NURBS description of contours. Int. J. Remote Sens. 2008, 29, 569–591. [Google Scholar] [CrossRef]
- Babaud, J.; Witkin, A.P.; Baudin, M.; Duda, R.O. Uniqueness of the Gaussian kernel for scale-space filtering. IEEE Trans. Pattern Anal. Mach. Intell. 1986, 1, 26–33. [Google Scholar] [CrossRef]
- Belongie, S.; Malik, J.; Puzicha, J. Shape matching and object recognition using shape contexts. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 509–522. [Google Scholar] [CrossRef]
- Huang, L.; Li, Z.; Zhang, R. SAR and optical images registration using shape context. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS2010), Honolulu, HI, USA, 25–30 July 2010; pp. 1007–1010.









| Method | Number of CPs | Polynomial Model | RMSE | Standard Deviation | Max Error | ||||||
| x | y | xy | x | y | xy | x | y | xy | |||
| SC | 31 | 1st-order | 1.92 | 1.88 | 2.69 | 1.92 | 1.88 | 1.06 | 3.46 | −3.97 | 4.39 |
| 2nd-order | 1.72 | 1.83 | 2.51 | 1.72 | 1.83 | 1.01 | 3.21 | −3.57 | 4.07 | ||
| SIFT | 9 | 1st-order | 2.33 | 2.73 | 3.59 | 2.33 | 2.73 | 1.88 | 4.08 | 5.34 | 6.72 |
| 2nd-order | 1.57 | 2.11 | 2.63 | 1.57 | 2.11 | 1.48 | −3.45 | −4.60 | 5.75 | ||
| SC+SIFT | 40 | 1st-order | 2.34 | 2.43 | 3.37 | 2.34 | 2.43 | 1.59 | −5.28 | 7.23 | 7.61 |
| 2nd-order | 2.22 | 2.31 | 3.21 | 2.22 | 2.31 | 1.33 | −4.35 | 6.74 | 7.05 | ||
| Method | Number of Check Points | Polynomial Model | RMSE | Standard Deviation | Max Error | ||||||
| x | y | xy | x | y | xy | x | y | xy | |||
| SC | 30 | 1st-order | 2.45 | 2.33 | 3.38 | 2.45 | 2.27 | 1.10 | −4.36 | −4.44 | 5.16 |
| 2nd-order | 3.00 | 2.43 | 3.86 | 2.98 | 2.34 | 1.50 | −7.34 | −4.98 | 7.35 | ||
| SIFT | 1st-order | 4.05 | 2.51 | 4.76 | 4.02 | 2.48 | 2.14 | 8.19 | 5.22 | 8.35 | |
| 2nd-order | 22.52 | 22.31 | 31.70 | 18.16 | 18.59 | 24.71 | 77.41 | 71.16 | 105.15 | ||
| SC+SIFT | 1st-order | 2.27 | 1.67 | 2.82 | 2.25 | 1.61 | 1.07 | 4.74 | −3.31 | 5.16 | |
| 2nd-order | 2.85 | 2.45 | 3.76 | 2.65 | 2.39 | 1.63 | 8.26 | −5.41 | 9.06 | ||
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rui, J.; Wang, C.; Zhang, H.; Jin, F. Multi-Sensor SAR Image Registration Based on Object Shape. Remote Sens. 2016, 8, 923. https://doi.org/10.3390/rs8110923
Rui J, Wang C, Zhang H, Jin F. Multi-Sensor SAR Image Registration Based on Object Shape. Remote Sensing. 2016; 8(11):923. https://doi.org/10.3390/rs8110923
Chicago/Turabian StyleRui, Jie, Chao Wang, Hong Zhang, and Fei Jin. 2016. "Multi-Sensor SAR Image Registration Based on Object Shape" Remote Sensing 8, no. 11: 923. https://doi.org/10.3390/rs8110923
APA StyleRui, J., Wang, C., Zhang, H., & Jin, F. (2016). Multi-Sensor SAR Image Registration Based on Object Shape. Remote Sensing, 8(11), 923. https://doi.org/10.3390/rs8110923