Ergodic Capacity of NOMA-Based Multi-Antenna LMS Systems with Imperfect Limitations
Abstract
:1. Introduction
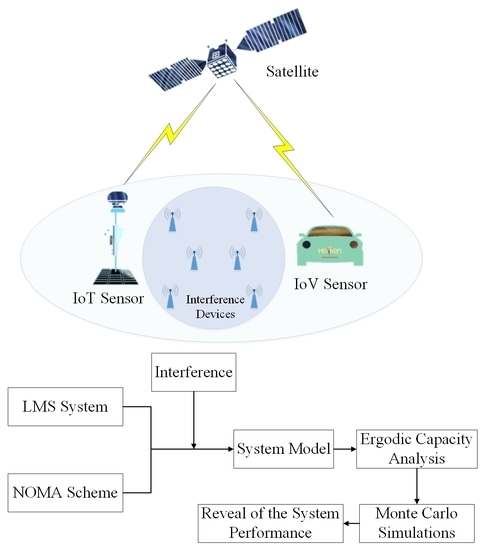
- Firstly, we illustrate a prevailing model for NOMA-based LMS systems under imperfect limitations. Imperfect SIC is analyzed due to the constraints of the receivers capability. Moreover, CEEs are considered owing to the imperfect CSI of the considered system. Along with the CEEs, another imperfect system limitations is considered due to frequency sharing, namely, CCI.
- Secondly, the analytical expression for EC of considered NOMA-based LMS systems is derived to evaluate the impacts of imperfect limitations on the performance of considered system. Moreover, the effects of CEEs, imperfect SIC, and CCI are revealed by theoretical results.
- Finally, the simulation results are further obtained to verify the efficiency and correctness of the theoretical results for the considered networks.
2. System Model
2.1. Channel Model
2.2. Signal Model
2.3. Problem Formulation
3. Performance Analysis
3.1. Preliminary Results
3.2. Ergodic Capacity Analysis
4. Numerical Results
5. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| 3GPP | Third Generation Partnership Project; |
| AFR | Array fed reflector; |
| AS | Average shadowing; |
| ASER | Average symbol error rate; |
| AWGN | Addictive white Gaussian noise; |
| CCI | Co-channel interference; |
| CDF | Cumulative distortion function; |
| CEEs | Channel estimation errors; |
| CSI | Channel state information; |
| DRA | Direct radiating array; |
| EC | Ergodic capacity; |
| EE | Energy efficiency; |
| FHS | Frequent heavy shadowing; |
| GEO | Geosynchronous earth orbit; |
| ILS | Infrequent light shadowing; |
| IoV | Internet of vehicles; |
| IoT | Internet of things; |
| IST-CD | Integrated satellite-terrestrial content delivery; |
| ISTN | Integrated satellite-terrestrial network; |
| ISTRN | Integrated satellite-terrestrial relay network; |
| LMS | Land mobile satellite; |
| LOS | Line-of-sight; |
| MC | Monte Carlo; |
| MMSE | Minimum mean square error; |
| MRC | Maximal Ratio Combining; |
| NOMA | Non-orthogonal multiple access; |
| OMA | Orthogonal multiple access; |
| OP | Outage probability; |
| Probability distribution function; | |
| QoS | Quality of service; |
| SatCom | Satellite communication; |
| SCT | Superposition coding technique; |
| SIC | Successive interference cancellation; |
| SINR | Signal to interference plus noise ratio; |
| SNR | Signal-to-noise ratio; |
| SR | Shadowed-Rician; |
| STNs | Satellite-terrestrial networks. |
References
- Jo, K.Y. Satellite Communications Netwowrk Design and Analysis; Artech House: Norwood, MA, USA, 2011. [Google Scholar]
- Lin, Z.; Lin, M.; de Cola, T.; Wang, J.-B.; Zhu, W.-P.; Cheng, J. Supporting IoT with rate-splitting multiple access in satellite and aerial integrated networks. IEEE Internet Things J. 2021, 8, 11123–11134. [Google Scholar] [CrossRef]
- Tse, D.; Viswanath, P. Fundamentals of Wireless Communication; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Guo, K.; An, K.; Zhang, B.; Huang, Y.; Tang, X.; Zheng, G.; Tsiftsis, T.A. Physical layer security for multiuser satellite communication systems with threshold-based scheduling scheme. IEEE Trans. Veh. Technol. 2020, 69, 5129–5141. [Google Scholar] [CrossRef]
- Lin, M.; Huang, Q.; de Cola, T.; Wang, J.-B.; Wang, J.Y. Integrated 5G-satellite networks: A perspective on physical layer reliability and security. IEEE Wirel. Commun. 2020, 27, 152–159. [Google Scholar] [CrossRef]
- Guo, K.; Lin, M.; Zhang, B.; Zhu, W.-P.; Wang, J.-B.; Tsiftsis, T.A. On the performance of LMS communication with hardware impairments and interference. IEEE Trans. Commun. 2019, 67, 1490–1505. [Google Scholar] [CrossRef]
- An, K.; Liang, T.; Yan, X.; Li, Y.; Qiao, X. Power allocation in land mobile satellite systems: An energy-efficient perspective. IEEE Commun. Lett. 2018, 22, 1374–1377. [Google Scholar] [CrossRef]
- Liu, R.; Guo, K.; An, K.; Zhu, S.; Shuai, H. NOMA-based integrated satellite-terrestrial relay networks under spectrum sharing environment. IEEE Wirel. Commun. Lett. 2021, 10, 1266–1270. [Google Scholar] [CrossRef]
- Guo, K.; An, K.; Zhou, F.; Tsiftsis, T.A.; Chatzainotas, S. On the secrecy performance of NOMA-based integrated satellite multiple-terrestrial relay networks with hardware impairments. IEEE Trans. Veh. Technol. 2021, 70, 3661–3676. [Google Scholar] [CrossRef]
- Yan, X.; Xiao, H.; An, K.; Zhen, G.; Chatzainotas, S. Ergodic capacity of NOMA-based uplink satellite networks with randomly deployed users. IEEE Syst. J. 2020, 14, 3343–3350. [Google Scholar] [CrossRef]
- Liu, Y.; Qin, Z.; Elkashlan, M.; Ding, Z.; Nallanathan, A.; Hanzo, L. Nonorthogonal multiple access for 5G and beyond. Proc. IEEE 2017, 105, 2347–2381. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Zhang, B.; An, K.; Zheng, G.; Chatzinotas, S.; Guo, D. Stochastic geometry-based analysis of cache-enabled hybrid satellite-aerial-terrestrial networks with non-orthogonal multiple access. IEEE Trans. Wirel. Commun. 2021. [Google Scholar] [CrossRef]
- Lu, W.; An, K.; Liang, T.; Yan, X. Robust beamforming in multibeam satellite systems with non-orthogonal multiple access. IEEE Wirel. Commun. Lett. 2020, 9, 1889–1893. [Google Scholar] [CrossRef]
- Singh, V.; Upadhyay, P.K.; Lin, M. On the performance of NOMA-assisted overlay multiuser cognitive satellite-terrestrial networks. IEEE Wirel. Commun. Lett. 2020, 9, 638–642. [Google Scholar] [CrossRef]
- Lin, Z.; Lin, M.; Wang, J.-B.; de Cola, T.; Wang, J. Joint beamforming and power allocation for satellite-terrestrial integrated networks with non-orthogonal multiple access. IEEE J. Sel. Top. Sig. Process. 2019, 13, 657–670. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Zhang, B.; An, K.; Zhao, B.; Guo, D. On the performance of hybrid satellite-terrestrial content delivery networks with non-orthogonal multiple access. IEEE Wirel. Commun. Lett. 2021, 10, 454–458. [Google Scholar] [CrossRef]
- An, K.; Lin, M.; Liang, T. On the performance of multiuser hybrid satellite-terrestrial relay networks with opportunistic scheduling. IEEE Commun. Lett. 2015, 19, 1722–1725. [Google Scholar] [CrossRef]
- Lin, Z.; Lin, M.; Champagne, B.; Zhu, W.-P.; Al-Dhahir, N. Secrecy-energy efficient hybrid beamforming for satellite-terrestrial integrated networks. IEEE Trans. Commun. 2021, 69, 6345–6360. [Google Scholar] [CrossRef]
- An, K.; Ouyang, J.; Lin, M.; Liang, T. Performance analysis of multi-antenna hybrid satellite-terrestrial relay networks in the presence of interference. IEEE Trans. Commun. 2015, 63, 4390–4404. [Google Scholar] [CrossRef]
- Guo, K.; Lin, M.; Zhang, B.; Cheng, J. Performance analysis of hybrid satellite-terrestrial cooperative networks with relay selection. IEEE Trans. Veh. Technol. 2020, 69, 9053–9067. [Google Scholar] [CrossRef]
- Famoriji, O.J.; Xu, Z. Antenna feed array synthesis for efficient communication systems. IEEE Sens. J. 2020, 20, 15085–15098. [Google Scholar] [CrossRef]
- Mouni, N.S.; Kumar, A.; Upadhyay, P.K. Adaptive user pairing for NOMA systems with imperfect SIC. IEEE Wirel. Commun. Lett. 2021, 10, 1547–1551. [Google Scholar] [CrossRef]
- Guo, K.; Kang, A.; Zhang, B.; Huang, Y.; Guo, D. On the performance of cognitive satellite-terrestrial relay networks with channel estimation error and hardware impairments. Sensors 2018, 18, 3292. [Google Scholar] [CrossRef] [Green Version]
- Huang, Q.; Lin, M.; Zhu, W.-P.; Cheng, J.; Alouini, M.-S. Uplink massive access in mixed RF/FSO satellite-aerial-terrestrial networks. IEEE Trans. Commun. 2021, 69, 2413–2426. [Google Scholar] [CrossRef]
- Solanki, S.; Upadhyay, P.K.; Costa, D.B.; Bithas, P.S.; Kanatas, A.G.; Dias, U.S. Joint impact of RF hardware impairments and channel estimation errors in spectrum sharing multiple-relay networks. IEEE Trans. Commun. 2018, 66, 3809–3824. [Google Scholar] [CrossRef]
- Liu, X.; Lin, M.; Zhu, W.-P.; Wang, J.-Y.; Upadhyay, P.K. Outage performance for mixed FSO-RF transmission in satellite-aerial- terrestrial networks. IEEE Photonic Tech. Lett. 2020, 32, 1349–1352. [Google Scholar] [CrossRef]
- Ruan, Y.; Jiang, L.; Li, Y.; Zhang, R. Energy-efficient power control for cognitive satellite-terrestrial networks with outdated CSI. IEEE Syst. J. 2021, 15, 1329–1332. [Google Scholar] [CrossRef]
- Ding, Z.; Schober, R.; Poor, H.V. Unveiling the importance of SIC in NOMA systems–Part 1: State of the art and recent findings. IEEE Commun. Lett. 2020, 24, 2373–2377. [Google Scholar] [CrossRef]
- Ding, Z.; Schober, R.; Poor, H.V. Unveiling the importance of SIC in NOMA systems–Part II: New results and future directions. IEEE Commun. Lett. 2020, 24, 2378–2382. [Google Scholar] [CrossRef]
- Shuai, H.; Guo, K.; An, K.; Zhu, S. NOMA-based integrated satellite terrestrial networks with relay selection and imperfect SIC. IEEE Access 2021, 9, 111346–111357. [Google Scholar] [CrossRef]
- Li, X.; Liu, M.; Deng, C.; Takis, P.; Liu, Y. Full-duplex cooperative NOMA relaying systems with I/Q imbalance and imperfect SIC. IEEE Wirel. Commun. Lett. 2020, 9, 17–20. [Google Scholar] [CrossRef]
- Yue, X.; Liu, Y.; Yao, Y.; Li, T.; Nallanathan, A. Outage behaviors of NOMA-based satellite network over shadowed-rician fading channels. IEEE Trans. Veh. Technol. 2020, 69, 6818–6821. [Google Scholar] [CrossRef] [Green Version]
- Ruan, Y.; Li, Y.; Wang, C.; Zhang, R.; Zhang, H. Energy efficient power allocation for delay constrained cognitive satellite terrestrial networks under interference constraints. IEEE Trans. Wirel. Commun. 2019, 18, 4957–4969. [Google Scholar] [CrossRef]
- Guo, K.; An, K.; Zhang, B.; Huang, Y.; Guo, D.; Zheng, G.; Chatzainotas, S. On the performance of the uplink satellite multiterrestrial relay networks with hardware impairments and interference. IEEE Syst. J. 2019, 13, 2297–2308. [Google Scholar] [CrossRef]
- Gradshteyn, I.S.; Ryzhik, I.M.; Jeffrey, A.; Zwillinger, D. Table of Integrals, Series, and Products, 7th ed.; Elsevier/Academic Press: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Vazquez, M.A.; Perez-Neira, A.; Christopoulos, D.; Chatzinotas, S.; Ottersten, B.; Arapoglou, P.D.; Ginesi, A.; Tarocco, G. Precoding in multibeam satellite communications: Present and future challenges. IEEE Wirel. Commun. 2016, 23, 88–95. [Google Scholar] [CrossRef] [Green Version]
- Abdi, A.; Lau, W.C.; Alouini, M.; Kaveh, M. A new simple model for land mobile satellite channels: First- and second-order statistics. IEEE Trans. Wirel. Commun. 2003, 2, 519–528. [Google Scholar] [CrossRef] [Green Version]
- Bletsas, A.; Shin, H.; Win, M.Z. Cooperative communication with outage-optimal opportunistic relaying. IEEE Trans. Wirel. Commun. 2007, 6, 3450–3460. [Google Scholar] [CrossRef] [Green Version]
- Huang, Q.; Lin, M.; Zhu, W.-P.; Chatzinotas, S.; Alouini, M.-S. Performance analysis of integrated satellite-terrestrial multiantenna relay networks with multiuser scheduling. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 2718–2731. [Google Scholar] [CrossRef]
- Farhadi, G.; Beaulieu, N.C. On the ergodic capacity of multi-hop wireless relaying systems. IEEE Trans. Wirel. Commun. 2009, 8, 2286–2291. [Google Scholar] [CrossRef]
- Prudnikov, A.P.; Brychkov, Y.A.; Marichev, O.I. Integralsand Series, Volume 3: More Special Functions; Gordon and Breach: New York, NY, USA, 1990. [Google Scholar]






| Parameter | Value |
|---|---|
| Satellite Orbit | GEO |
| Carrier Frequency | 18 GHz |
| Carrier Bandwidth | B = 50 MHz |
| 3 dB angle | |
| Maximal Beam Gain | = 48 dB |
| Receive Antenna Gain | = 4 dB |
| Noise Temperature | T = 300 K |
| Rain Attenuation |
| Shadowing | |||
|---|---|---|---|
| Frequent heavy shadowing (FHS) | 1 | 0.063 | 0.0007 |
| Average shadowing (AS) | 5 | 0.251 | 0.279 |
| Infrequent light shadowing (ILS) | 10 | 0.158 | 1.29 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shuai, H.; Liu, R.; Zhu, S.; Li, C.; Fang, Y. Ergodic Capacity of NOMA-Based Multi-Antenna LMS Systems with Imperfect Limitations. Sensors 2022, 22, 330. https://doi.org/10.3390/s22010330
Shuai H, Liu R, Zhu S, Li C, Fang Y. Ergodic Capacity of NOMA-Based Multi-Antenna LMS Systems with Imperfect Limitations. Sensors. 2022; 22(1):330. https://doi.org/10.3390/s22010330
Chicago/Turabian StyleShuai, Haifeng, Rui Liu, Shibing Zhu, Changqing Li, and Yi Fang. 2022. "Ergodic Capacity of NOMA-Based Multi-Antenna LMS Systems with Imperfect Limitations" Sensors 22, no. 1: 330. https://doi.org/10.3390/s22010330
APA StyleShuai, H., Liu, R., Zhu, S., Li, C., & Fang, Y. (2022). Ergodic Capacity of NOMA-Based Multi-Antenna LMS Systems with Imperfect Limitations. Sensors, 22(1), 330. https://doi.org/10.3390/s22010330