Abstract
This study considers a manufacturer–retailer–streamer supply chain, in which the retailer first purchases products from a manufacturer and then sells them to consumers through a streamer. In the live streaming context, the retailer usually cooperates with the streamer by providing three different contracts: only a commission of the sale (OC), only a fixed fee (OF), and a commission of the sale and fixed fee (CF). Therefore, this study develops a theoretical model to investigate the effects of these three contracts on supply chain members’ optimal decisions and profits. The following results were obtained: (1) the retailer prefers an OC contract with a high-ability streamer, and the manufacturer benefits from this contract. Additionally, the manufacturer, retailer, and high-ability streamer can achieve a win–win–win outcome in certain cases. Furthermore, the retailer is willing to sign an OC contract with a low-ability streamer when the fixed fee of the OF contract is high. (2) The retailer prefers to cooperate with a low-ability streamer through an OF contract when the fixed fee is low. (3) The CF contract is the most profitable alternative for the retailer when the total commission rate is low and the fixed fee is medium.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Due to rapid advances in digital technology, a growing number of consumers, especially young people, prefer online shopping. Given the recent COVID-19 outbreak, contactless online shopping has become increasingly popular. Numerous retailers invest heavily in online sales technology to make online shopping more convenient and thereby attract more consumers. For example, several retailers employ professional salespeople to provide product information in online stores, thereby enhancing consumers’ awareness of products.Footnote 1 A new online marketing method called live streaming has been developed recently. The associated shopping method has become prevalent and attracted several consumers and firms. In China, approximately 309 million viewers were immersed in live streaming in June 2020—an increase of 16.7% since March 2020. The user traffic in live streaming will be over 2.5 million on average by 2020 [2]. Numerous firms are scrambling to live streaming to promote their products, including Huawei, GREE, Xiaomi, and La Mer.Footnote 2 Consequently, the live streaming transaction for one year was over 100 million RMB (US$15.4 million) until March 31, 2021.Footnote 3 Cooperation with professional streamers can create high sales records for firms and enhance the popularity of their brands. For example, Viya sold 10,000 Honey for Richora in the first 5 s during live streaming, and Austin Li sold 15,000 lipsticks in just 15 min during live streaming.Footnote 4
However, firms cooperating with streamers to sell products through live streaming are not always successful. Occasionally, the firm’s profit from live streaming shopping cannot offset the high cost of employing a streamer. For example, Zebra AI, an online education firm, invited Luo to live streaming with high pit fees (1.2 million RMB). However, Luo only brought in sales worth 529,200 yuan—less than half of the pit fees and far below the firm’s expectations [9]. A thermos brand spent 100,000 yuan engaging Huang Shengyi to sell its products via live streaming,however, she only sold five thermoses, thus causing a major loss for the firm.Footnote 5 Therefore, spending a high fixed fee to cooperate with a celebrity does not imply the success of live streaming. Successful live streaming shopping is determined by several factors, such as the streamer’s proficiency in sales skills, the number of prospective consumers present during the live streaming, and, most importantly, the contract between firms and streamers. The contracts clarify the rights and obligations of retailers and streamers. Based on the contract agreement, retailers must pay streamers’ salaries, and streamers promise to help retailers promote and sell the latter’s products through live streaming. A reasonable contract can motivate the streamer to make efforts to sell products during live streaming. Therefore, an evident question arises: What kind of contract should the retailer choose? In this study, we predominantly aim to investigate this question.
In practice, retailers are likely to cooperate with the streamer through three different contracts: only a commission of the sale (OC), only a fixed fee (OF), and a commission of the sale and fixed fee (CF). Such contracts are widely used by retailers. For example, (1) OC contract: A clothing merchant cooperated with Tiktok’s streamers through a pure commission.Footnote 6 (2) OF contract: A massage equipment firm paid a pit fee of 500,000 yuan to invite Chen Xiaochun to sell its products in a live stream. (3) CF contract: A smart home merchant engaged Sydney to sell its products by paying a pit fee of 10,000 yuan and 20% commission.Footnote 7 Different contracts have different incentives for the streamers. The OC contract motivates the streamer to sell products when the unit commission of sale is considerable; however, a high sales commission is detrimental to firms’ profits. By signing the OF contract with a streamer, the retailer must bear a fixed fee regardless of the sale of the products. Therefore, the CF contract is popular in that the firm need not bear a high fixed fee, and the unit commission of the sale also motivates the streamer to sell the products more aggressively. However, determining the proportion of the unit commission of sales and the fixed fee is a key problem for firms. Different contracts have different effects on supply chain members’ decisions and profits. Therefore, the following research questions arise: What contract strategies should the retailer adopt, and how do these strategies affect the retailer’s decisions regarding product pricing? How much effort should streamers invest in live streaming? How do the total commission rates of sales and fixed fees affect retailers’ decisions?
This study considers a manufacturer-retailer-streamer supply chain to answer the aforementioned research questions. The retailer purchases products from a manufacturer and engages a streamer to sell products to viewers through live streaming. The retailer and streamer establish a cooperative relationship for live steaming through a contract. Specifically, the three common contracts mentioned above are considered: only a commission of the sale (OC), only a fixed fee (OF), a commission of the sale and a fixed fee (CF). First, we examine the equilibrium outcomes by analyzing different cooperative contracts. We then investigate the effects of cooperative contracts on supply chain members’ optimal decisions and profits. We further discuss the conditions under which the retailer (streamer) should adopt (accept) a certain contract.
This study’s analysis provides significant managerial insights. First, under an OC contract, the retailer prefers raising the product price to obtain more profits. The retailer is willing to sign this contract with a high-ability streamer who can generate the largest product demand and, consequently, profits. Under this case, the manufacturer get a “free ride”; that is, the manufacturer can earn greater profits by increasing the wholesale price. Second, the retailer is willing (reluctant) to cooperate with a low-ability streamer when the fixed fee for the OF contract is low (high). The OF contract can drive the largest product demand for retailers and manufacturers for a low-ability streamer. Third, the CF contract is the most profitable alternative for the retailer when the total commission rate is low and the fixed fee is medium. Finally, the manufacturer, retailer, and high-ability streamer can achieve a win–win–win outcome in the following case: The retailer cooperates with the high-ability streamer through the OC contract, and the fixed fee of the OF contract is small. These managerial insights shed light on the problem of cooperative contracts between retailers and streamers.
Our contribution to the literature on live-stream sales is threefold. (1) The current literature on e-commerce live streaming does not focus on the different cooperative contracts between streamers and retailers. Our study is the first to explicitly explore the issues of different cooperation contracts in e-commerce live streaming, thus filling the related research gap. (2) Our study considers three types of common contracts and examines the retailer’s contract selection decisions endogenously. We explore how the retailer chooses different contracts. (3) We study the influence of different cooperative contracts on a firm’s optimal pricing decisions and a streamer’s efforts. The conclusions derived from this study provide a decision-making reference for firms to implement e-commerce live streaming with “Internet celebrities”.
This paper is organized as follows: we analyze and summarize the literature related to live streaming and our paper’s contributions in Sect. 2. Section 3 describes the differences among the three contract models. In Sect. 4, we derive the equilibrium price strategies and explore the impacts of product demand and the optimal streamer’s effort on contract strategies. Finally, Sect. 5 summaries the optimal contract strategy under certain conditions and concludes the paper. All relevant proofs are shown in Appendix.
2 Literature review
This study explores the effects of different contracts on channel members’ decisions and profits during live streaming. This study contributes to the literature on live streaming and supply chain contracts.
2.1 Live streaming
Live streaming, as a new and contactless retail strategy, has received considerable attention in academia. Most extant literature on live streaming has focused on empirical research. Examining shopping intentions and reasons stimulated by live streaming has been a key direction in this research area (e.g., [20, 29, 44]). Chen and Lin [6] conducted empirical research to explore audience motivation to participate in live streaming. Sun et al. [37], in their empirical analysis, highlighted the importance of live streaming in driving purchase intention and, thus, in increasing sales. Kim and Kim [21] developed an empirical model to explore the impact of e-sport watching motivation on the viewing experience. Chen et al. [7] empirically explored the factors influencing consumers’ shopping intentions to purchase products during live streaming, including expertise, similarity, and likeability. Addo et al. [8] found that social elements positively influence customer purchase intentions. Ma [31] utilized a structural model to study how a live stream arouses consumers’ willingness to purchase.
Another research direction empirically explores the interaction between viewers and streamers during live streaming (e.g., [35, 40]). Yu et al. [47] and Li et al. [22, 23, 25] found that viewers' participation in live streaming is positively related to them sending gifts to the streamers. Hu and Chaudhry [17] evaluated the importance of enhancing relational bonds in consumer engagement. Wongkitrungrueng et al. [41] examined the optimal strategy for retailers to acquire and retain customers. Lu et al. [30] studied the impact of the number of viewers on tipping revenue. Kang et al. [19] adopted a framework to show how interactivity affects consumer behavior.
Most aforementioned research has focused on shopping intention and live-stream interaction. Few studies have assessed optimal contracts between firms and streamers using theoretical model analysis in the extant literature. The following two studies are related to our study: Wang et al. [39] studied whether a streamer should join a platform by considering two different salary mechanisms using a game model, wherein when a streamer joins a platform, equilibrium outcomes are derived. They showed that streamers at all ability levels would join the platform if the sharing rate and basic salary were high. They demonstrated a case wherein an increment in the sharing rate would increase the amount of effort that streamers exerted. Instead of emphasizing whether the streamer joins the platform, our study focuses on the contracts signed between retailers and streamers. More recently, Liu and Liu [28] explored the optimal decisions of platforms and streamers using differential game theory. They showed that setting a high sharing rate is harmful to a platform. They presented a subsidy mechanism under which streamers and the platform can achieve a win–win outcome. Liu and Liu [28] only considered a type of revenue-sharing mechanism with a sharing rate,in contrast, we study the case in which a retailer provides different contracts to the streamers by analyzing three scenarios. While the above two studies considered the contracts that streamers sign with the platform, we assume a case wherein streamers directly sign with the retailer.
2.2 Revenue-sharing contracts
The revenue-sharing contract is considered an important factor in cooperation in the supply chain. The widespread literature on revenue-sharing contracts is closely related to our research. Cai et al. [4] found that a revenue-sharing contract would make supply chain members competitive when comparing revenue-sharing and supplier subsidy contracts. Song and Gao [36] investigated the role of revenue-sharing contracts in improving performance in a green supply chain. Heydari and Ghasemi [16] found that a revenue-sharing contract can create a win–win outcome when re-manufacturing capacity is limited. Fatehi and Wagner [11] found that a revenue-sharing contract is more suitable for crowdfunding than other financing models. Tsao and Lee [38] concluded that a revenue-sharing contract impacts manufacturers and retailers when facing uncertain demand. Panja and Mondal [34] studied a two-layer green supply chain with a credit link demand. Liu et al. [27] compared revenue-sharing and cost-sharing contracts to determine which contract improves product greenness. Additionally, a few studies have considered multiple periods [26, 33], information sharing [43, 49], and dual channels [5, 42] under revenue-sharing contracts. Several studies have examined carbon emissions under revenue-sharing contracts [3, 24, 45]. The aforementioned studies have examined the function of revenue-sharing contracts in different contexts, while the problem of revenue-sharing contracts in a live streaming environment has not been investigated. Our study considers the influence of revenue-sharing contracts on streamers’ efforts and pricing decisions of manufacturers and retailers, which expands the research on revenue-sharing contracts.
2.3 Difference between our work and existing literature
Our study differs from the aforementioned studies in the following four respects. (1) Extant studies associated with live-stream selling have empirically focused on shopping intention and live-stream interaction; our study considers the optimal contracts between firms and streamers through theoretical model analysis. (2) Our study is the first to explicitly explore the issues of different types of contracts in e-commerce live streaming. (3) Most extant research has concentrated on improving supply chain performance by only a type of revenue-sharing contract; however, our study compares different cooperation contracts and analyzes their impact on the firm’s live-stream strategies.
3 Models
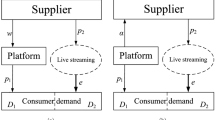
We consider a manufacturer-retailer-streamer supply chain, in which the retailer purchases products at wholesale price \(w\) from the manufacturer and then engages a streamer to sell the products to the viewers at unit price \(p\) through live streaming. For simplicity, the retailer employs only one streamer, and every individual viewer during live streaming buys at most one product. Additionally, the marginal production cost is assumed to be constant and zero—a commonly held assumption in related studies (e.g., [10, 18, 22, 23, 32, 46]). In this study, we examine three different contracts—OC, OF, and CF—between the retailer and streamer; thereafter, we use subscripts \(m\), \(r,\) and \(s\) to denote the manufacturer, retailer, and streamer, respectively.
All the notations in this paper are summarized in Table 1.
The decision sequence for our model is shown in Fig. 1. First, the retailer decides which contract (OC, OF, or CF) to sign with the streamer. Second, the manufacturer decides the wholesale price \(w\). Third, the retailer sets the product retail price \(p\), and the streamer decides their effort \(e\) during live streaming. Finally, the viewer evaluates the product during live streaming and decides whether to buy it. The wholesale price \(w\), streamer effort \(e\), and live streaming price \(p\) are decision variables, whereas the others are exogenous.
In our model, viewers are heterogeneous regarding product valuation \(v\), and \(v\) is distributed uniformly over [0, 1], which can also be found in previous studies [14, 43]. Streamers’ attractiveness, interaction, effort, and expertise can increase viewers’ willingness to buy [12, 28, 44]. Thus, the utility function of viewers purchasing a product during live streaming is denoted as:
where \(b\) denotes the sensitivity coefficient of the streamer’s effort \((b>0)\) and \(be\) represents the improvement in viewers’ utility due to streamers’ live-streaming efforts. If \(u>0\), viewers will purchase the product in live streaming; otherwise, they will not place an order. From the utility function of viewers, we derive the demand function of products in live streaming:
Equation (2) shows that the streamer’s effort positively influences demand for the product in live streaming.
In our model, the streamer’s profits comprise two parts: salary and gifts (tip). On the one hand, after the streamer signs a contract with the retailer, the former obtains a salary from the latter. Based on the type of contract (OC, OF, or CF), the streamer’s salary differs, including only the commission of the sale, fixed fee, and part commission of sale and fixed fee. During live streaming, viewers appreciate the streamer’s effort to sell products and, thus, buy and send virtual gifts to the streamer. For example, Dong Mingzhu, a Gree Electric Appliances chairwoman, received a tip of 3,407 million virtual currency (about 340,000 yuan) from viewers as a reward for a live-stream selling.Footnote 8 Following Wang et al. [39], the profit of the streamer from gifts is presented as
where \(s\) \((s>0)\) represents the efficiency of the streamer receiving gifts (tips) from viewers. The efficiency \(s\) is determined by the streamer’s fame; that is, a famous streamer exhibits high efficiency. Further, \(e\) represents the streamer’s live streaming efforts. In our model, the streamer’s effort in live streaming incurs a cost:
Note that the cost follows a quadratic form commonly found in previous studies [13, 15]. Parameter \(c\) denotes the cost coefficient of the streamer’s effort and reflects the streamer’s ability [39]. The higher the streamer’s ability, the smaller the effort cost. The streamer’s ability is high when the \(c\) is less. Next, we study the channel members’ optimal decisions under the following three contracts: OC, OF, and CF.
3.1 OC contract
In the OC contract (model OC), the retailer offers only a unit commission of sale \(r\) as a salary to the streamer. Under this contract, the streamer receives a commission \(r\) from the retailer for each product sold through live streaming. In particular, the more streamers sell through live streaming, the more profits they will obtain. Thus, the streamer’s profits in model OC can be formulated as
In addition to the profit of the commission of the sale, the streamer’s total profits include profits of the gifts (tips) and the cost of the streamer’s effort during live streaming. The profit function with respect to the retailer under the OC contract is.
Note that \(w\) represents the wholesale price and \(r\) denotes the unit sale commission. The manufacturer’s profit function is given by
By resolving Eqs. (5)–(7), we obtain the optimal wholesale price, retail price, and streamer effort under the OC contract, as shown in Table 2. The profits of the manufacturer, retailer, and streamer in Model OC are presented in Table 3.
3.2 Model OF
In the OF contract (model OF), the retailer only provides a fixed fee \(k\) to the streamer as his salary. The streamer promises to help the retailer promote and sell products through live streaming. An OF contract is generally used to cooperate with a famous streamer, who can help the retailer and manufacturer clear inventory and enhance the popularity of products in live streaming, thus benefitting the retailer. Thereafter, the streamer’s profits under model OF is given by:
Similarly, in addition to the fixed fee \(k\), the streamer’s total profits include the profit of the gifts (tips) and the cost of the streamer’s effort. The retailer’s profit is:
Then, the profit function regarding the manufacturer is represented as:
The optimal wholesale price, retail price, and the streamer’s effort in the OF model are presented in Table 2. The product demand and profits of the manufacturer, retailer, and streamer are shown in Table 3.
3.3 Model CF
In the CF contract (model CF), the retailer not only shares a commission of sale \(\beta r\) with the streamer but also offers a fixed fee \(\alpha k\) to the streamer. The streamer’s total profits in this scenario comprise the fixed fee \(\alpha k\), the unit commission of sale \(\beta r\) and gifts(tips). The CF contract is commonly used in practice because the variety of streamers’ profits can enhance their motivation for live streaming. The unit commission of sale \(\beta r\) indicates that the streamer may gain greater profit from product sales through their efforts. The streamer receives a fixed fee \(\alpha k\) as part of their salary. Hence, we can formulate the profits of the streamer, which are given by:
The profits function of the manufacturer and retailer are as follows:
and
By resolving Eqs. (11)–(13), respectively, we can derive the optimal wholesale price, retail price, and streamer effort, respectively, which are shown in Table 2; consequently, we obtain the optimal profit of the manufacturer, retailer, and streamer under the CF model, which is also presented in Table 3.
4 Analysis
This section examines the effects of the different contracts (OC, OF, and CF) on the optimal wholesale price, retail price, streamer effort, and product demand and then examine the optimal contract strategy for supply chain members.
Proposition 1
The streamer’s optimal effort, retail price, and wholesale price under different contracts meet the following properties:
-
(i)
\({e}^{OF*}<{e}^{CF*}<{e}^{OC*}\);
-
(ii)
\({p}^{OF*}<{p}^{CF*}<{p}^{OC*}\);
-
(iii)
if \(c<{b}^{2}\), we have \({w}^{OF*}<{w}^{CF*}<{w}^{OC*}\); if \(c>{b}^{2}\), we have \({w}^{OF*}>{w}^{CF*}>{w}^{OC*}.\)
Proposition 1(i) shows that the streamer’s optimal effort under an OC contract is the largest and that under an OF contract is the smallest. This can be explained as follows: Under the OC contract, the streamer receives a commission of sale \(r\) when they sell one product through live streaming. The more products they sell, the more commission they receive. The commission of sale \(r\) can stimulate the streamer to exert greater effort during live streaming. Therefore, the streamer’s optimal effort under the OC contract is the largest.
Proposition 1(ii) shows the same relationship as Proposition 1(i) for the optimal product price. The product price under the OC contract is higher than the other contracts. Specifically, the retailer prefers increasing the product price as the streamer's effort increases. Hence, the retailer may increase the product price due to the presence of an OC contract.
Proposition 1(iii) indicates that if the streamer’s effort cost (\(c\)) is sufficiently small, that is, \(c<{b}^{2}\), the wholesale price under the OC contract is the largest among these contracts. Combining the results of Proposition 1(i)–(iii), we find that the streamer’s optimal effort under the OC contract is the largest. A high-ability streamer can persuade more viewers to buy products during live streaming. Thus, the manufacturer tends to offer a high wholesale price when the retailer cooperates with a high-ability streamer through the OC contract. However, the result is the opposite when the retailer cooperates with a low-ability streamer. Specifically, a low-ability streamer cannot persuade more viewers to buy products during live streaming, even if the streamer’s optimal effort under the OC contract is the largest.
Different cooperative contracts also have different influences on product demand in live streaming. Therefore, we compare product demand under different contracts and obtain Proposition 2.
Proposition 2
The product demand under different contracts exhibits the following relationship:
-
(i)
if \(c<{b}^{2}\), we have \({D}^{OF*}<{D}^{CF*}<{D}^{OC*}\);
-
(ii)
if \(c>{b}^{2}\), we have \({D}^{OF*}>{D}^{CF*}>{D}^{OC*}\).
Proposition 2(i) shows that product demand is the largest when the retailer signs an OC contract with a high-ability streamer. Product demand is also the largest for an OF contract with a low-ability streamer. This is because an OC contract can stimulate high-ability streamers exert maximal efforts to sell products, and high-ability streamers can persuade more viewers to buy products through their proficient sales skills. Proposition 2(ii) indicates that the sale of products under the OC contracts is smallest when the streamer’s ability is low. Although the OC contract can stimulate low-ability streamers to try their best to sell products, low-ability streamers cannot persuade more viewers to buy products. Thus, the opposite result is obtained.
Propositions 1 and 2 indicate the effects of different contracts (OC, OF, and CF) on the optimal wholesale price, retail price, the streamer’s effort, and product demand. Then, we examine the retailer’s optimal contract strategy in Proposition 3.
Proposition 3
The optimal contract strategy for the retailer by comparing the retailer’s profit under the different contracts satisfies the following relationship:
-
(i)
When \(c<{b}^{2}\), we have \({\pi }_{r}^{OC}>{\pi }_{r}^{CF}>{\pi }_{r}^{OF}\).
-
(ii)
When \(c>{b}^{2}\) and \(\alpha +\beta >1\), we have \({\pi }_{r}^{CF}<max {(\pi }_{r}^{OF},{\pi }_{r}^{OC})\). Furthermore, \({\pi }_{r}^{OC}>{\pi }_{r}^{OF}\), if \(k>{k}_{OF-OR}\); otherwise, \({\pi }_{r}^{OF}>{\pi }_{r}^{OC}\).
-
(iii)
When \(c>{b}^{2}\) and \(\alpha +\beta <1\),
(a) if \(k>{k}_{CF-OC}\), \({\pi }_{r}^{OC}>max ({\pi }_{r}^{CF},{\pi }_{r}^{OF})\).
(b) if \({k}_{CF-OF}<k<{k}_{CF-OR}\), \({\pi }_{r}^{CF}>max ({\pi }_{r}^{OF},{\pi }_{r}^{OC})\).
(c) if \(k<{k}_{CF-OF}\), \({\pi }_{r}^{OF}>max ({\pi }_{r}^{CF},{\pi }_{r}^{OC})\).
Note that \({k}_{OF-OC}\), \({k}_{CF-OC}\), \({k}_{CF-OF}\) are the fixed fee thresholds among model OC, OF, and CF for the retailer. \({k}_{CF-OF}=\left(\left(r\left({b}^{2}-c\right)\beta +2bs+2c\right)\beta \left(c-{b}^{2}\right)r\right)/16{c}^{2}\left(1-\alpha \right)\), \({k}_{OF-OC}=\left(\left({b}^{2}r+2bs-c\left(r-2\right)\right)\left(c-{b}^{2}\right)r\right)/16{c}^{2}\), and \({k}_{CF-OC}=((\left(-r\beta -r+2\right)c+\left(r\left(\beta +1\right)b+2s\right)b)\left(1-\beta \right)\left(c-{b}^{2}\right)r)/16{c}^{2}\).
Proposition 3(i) shows that if the streamer’s effort cost (\(c\)) is less than a threshold, that is, \({b}^{2}\), the retailer’s profit under the OC contract is larger than that under other contracts. Specifically, high-ability streamers under the OC contract can generate the highest profit for the retailer. Combined with Propositions 1 and 2, we find that signing an OC contract can increase product price and demand. An increase in demand increases the retailer’s total profits. Therefore, the retailer is willing to sign an OC contract with a high-ability streamer.
The high cost of the streamer’s effort (\(c\)) implies that the streamer’s ability is relatively low. Therefore, Proposition 3(ii) indicates that if the total commission rate of sales and fixed fee (\(\alpha +\beta\), hereafter, the total commission rate) is sufficiently large, i.e., \(\alpha +\beta >1\), the retailer's profit under the CF contract is invariably less than that under the OC and OF contracts, indicating that the retailer is unwilling to sign the CF contract with a low-ability streamer when the total commission rate is relatively large. A low-ability streamer cannot persuade more viewers to buy products during live streaming, even if they sign a CF contract with a high total commission rate. The retailer also must bear the streamer’s high salary, which is detrimental for the retailer. As far as the OF and OC contracts are concerned, when the fixed fee is larger (smaller) than the threshold, that is, \({k}_{OF-OC}\), the OC (OF) contract is beneficial for the retailer. Intuitively, the retailer signs the OF contract for a low-ability streamer when the fixed fee is large. Consequently, the retailer can reduce costs and increase profits.
Proposition 3(iii) shows that the type of contracts signed by the retailer depends on the fixed fee when the total commission rate is less than one and the streamer’s ability is low. Signing the OC contract benefits the retailer when the fixed fee is high (i.e., \(k>{k}_{CF-OC}\)). If the fixed fee is medium, that is, \({k}_{CF-OF}<k<{k}_{CF-OC}\), the retailer’s profit under the CF contract is higher than that under the others. When the fixed fee is relatively low, i.e., \(k<{k}_{CF-OF}\), signing the OF contract is profitable for the retailer. The retailer may obtain less profit and even take greater risks if he offers a high fixed fee to a low-ability streamer and vice versa. The profit brought about by a low-ability streamer in live streaming cannot offset the expensive fixed fee. Thus, the retailer does not prefer to sign the OF contract with a low-ability streamer when the fixed fee is sufficiently high. Combining Propositions 2 and 3, we report an interesting finding: For a low-ability streamer, although product demand under the OF contract is the largest, the retailer's profit is not the highest. In practice, some retailers participate in live streaming for increasing sales and enhancing their products’ popularity, not for earning short-term profits.
Proposition 3 describes the retailer’s optimal profit under different contracts and associated conditions. Next, we describe the streamer’s contract strategy in Proposition 4.
Proposition 4
The optimal contract strategy for the streamer by comparing the streamer’s profit under the different contracts has the following relationship:
-
(i)
When \(\alpha +\beta >1\), we have (a) if \(k>{k}_{CF-OF}^{^{\prime}}\), \({\pi }_{s}^{OF}>max ({\pi }_{s}^{CF},{\pi }_{s}^{OC}).\)(b) if \({k}_{CF-OC}^{^{\prime}}<k<{k}_{CF-OF}^{^{\prime}}\), \({\pi }_{s}^{CF}>max ({\pi }_{s}^{OF},{\pi }_{s}^{OC})\) (c) if \(k<{k}_{CF-OC}^{^{\prime}}\), \({\pi }_{s}^{OC}>max ({\pi }_{s}^{CF},{\pi }_{s}^{OF}).\)
-
(ii)
When \(\alpha +\beta <1\), we have (a) if \(s>{s}_{1}\), \({\pi }_{s}^{CF}<{max (\pi }_{s}^{OF},{\pi }_{s}^{OC})\). Furthermore, \({\pi }_{s}^{OC}>max ({\pi }_{s}^{CF},{\pi }_{s}^{OF})\), if \(k<{k}_{OF-OC}^{^{\prime}}\); otherwise, \({\pi }_{s}^{OF}>max ({\pi }_{s}^{CF},{\pi }_{s}^{OC})\). (b) if \(s<{s}_{1}\) And 0 \(<r<{r}_{2}\), \({\pi }_{s}^{CF}<{max (\pi }_{s}^{OF},{\pi }_{s}^{OC})\); if \(s<{s}_{1}\), and \({r}_{2}<r<1\), the result is the same as proposition 4(i), i.e., if \(k>{k}_{CF-OF}^{^{\prime}}\), \({\pi }_{s}^{OF}>max ({\pi }_{s}^{CF},{\pi }_{s}^{OC})\); if \({k}_{CF-OC}^{^{\prime}}<k<{k}_{CF-OF}^{^{\prime}}\), \({\pi }_{s}^{CF}>max ({\pi }_{s}^{OF},{\pi }_{s}^{OC})\) and; if \(k<{k}_{CF-OC}^{^{\prime}}\), \({\pi }_{s}^{OC}>max ({\pi }_{s}^{CF},{\pi }_{s}^{OF}).\)
Note that \({k}_{OF-OC}^{^{\prime}}\), \({k}_{CF-OC}^{^{\prime}}\), \({k}_{CF-OF}^{^{\prime}}\) are the fixed fee thresholds among model OC, OF, and CF for the streamer. \({k}_{OF-OC}^{^{\prime}}=r\left(-{b}^{2}r+bs-cr+c\right)/(4c)\); \({k}_{CF-OC}^{^{\prime}}=\left(\beta -1\right)\left(\left(\beta +1\right)\left({b}^{2}+c\right)r-bs-c\right)r/(4c\alpha )\); \({k}_{CF-OF}^{^{\prime}}=\beta r\left(r\left({b}^{2}+c\right)\beta -bs-c\right)/\left(4c(\alpha -1)\right)\).\({s}_{1}=({b}^{2}+c){\beta }^{2}-\beta c+{b}^{2}\left(\alpha -1\right)/((\beta +\alpha -1)b)\), and \({r}_{2}=(\beta +\alpha -1)\left(bs+c\right)/(({\beta }^{2}+\alpha -1)({b}^{2}+c))\).
Proposition 4(i) implies that the streamer’s optimal contract strategy varies with the fixed fee when the total commission rate is higher than 1. More specifically, the CF contract is most profitable for the streamer only if the fixed fee is at an intermediate level—that is, \({k}_{CF-OC}^{^{\prime}}<k<{k}_{CF-OF}^{^{\prime}}\). When the fixed fee is at a high level, that is, \(k>{k}_{CF-OF}^{^{\prime}}\), the streamer will benefit the most from signing the OF contract. If the fixed fee is less than the threshold \({k}_{CF-OR}^{^{\prime}}\), the profit of the streamer under the OC contract is higher than that of the other contract types. Thus, the type of contract advantageous to the streamer depends on the value of the fixed fee; this point is intuitive and realistic. The streamer signs a contract with (without) a fixed fee when the fixed fee is high (low). Compared to Proposition 3(ii), when the total commission rate is larger than 1, the CF contract is unfavorable for the retailer under any condition. Meanwhile, the streamer signing the CF contract can earn more profits than other contracts if the fixed fee is at the intermediate level.
The low total commission rate makes it difficult for the streamer to obtain more profits from the CF contract. Thus, Proposition 4(ii) indicates that the streamer would be reluctant to sign the CF contract with the retailer unless the unit commission of sale \(r\) is relatively large, the fixed fee \(k\) is medium, and the efficiency of getting gifts \(s\) is relatively low. We explain this as follows: First, under the certain condition (the total commission rate is low), the streamer gains more profits from the CF contract when the unit commission of sale \(r\) is relatively small. An excessively high fixed fee would increase the OF contract’s profit to a level higher than the CF contract’s profit. As mentioned earlier, famous streamers exhibit high efficiency. Famous streamers prefer the OF contract to the CF contract. Therefore, the streamer gains the highest profit from the CF contract when the total commission rate is low, unless the condition is satisfied. Compared with Proposition 3, we find that the retailer and a high-ability streamer can achieve a win–win outcome. Specifically, the profits of the retailer and streamer are highest when the retailer cooperates with a high-ability streamer through the OC contract and the fixed fee of the OF contract is low. Further, product demand is also the highest.
To explore how the different contracts between the streamer and retailer influence the manufacturer, we present Proposition 5.
Proposition 5
The manufacturer’s profit under the OC contract is the highest when \(c<{b}^{2}\); otherwise, the manufacturer’s profit under the OF contract is the highest. Furthermore, the manufacturer’s profit under the CF contract is always intermediate. Specifically, if \(c<{b}^{2}\), we have \({\pi }_{m}^{OC}>{\pi }_{m}^{CF}>{\pi }_{m}^{OF}\); if \(c>{b}^{2}\), we have \({\pi }_{m}^{OC}<{\pi }_{m}^{CF}<{\pi }_{m}^{OF}\).
As Proposition 5 shows, the OC contract is most profitable for the manufacturer when the streamer’s effort cost \(c\) is small (i.e., the streamer’s ability is high). With Propositions 1 and 2, we find that the manufacturer offers the highest wholesale price when the retailer cooperates with a high-ability (low-ability) streamer through an OC (OF) contract. Product demand under the OC (OF) contract is also the highest when the streamer’s ability is high (low). Therefore, the OF (OC) contract is most beneficial to the manufacturer when the streamer’s ability is high (low). Combining Propositions 3, 4, and 5, we find that the manufacturer’s profit is the largest when the retailer and high-ability streamer achieve a win–win outcome.
5 Conclusions
This study considers a manufacturer-retailer-streamer supply chain, in which the retailer purchases products from a manufacturer and sells products cooperating a streamer through live streaming. In practice, the retailer is likely to cooperate with the streamer by signing one of three different contracts: a commission of the sale (OC), a fixed fee (OF), and a part commission of the sale and a fixed fee (CF). Therefore, this study develops a theoretical model to investigate the effects of these three contracts on supply chain members’ optimal decisions and profits. The main findings and insights are as follows.
Optimal decisions under the three contracts: First, we show that the streamer’s optimal effort under the OC contract is the largest and that under the OF contract is the smallest. This is because a sales commission can stimulate the streamer to exert greater effort during live streaming. Second, the product price under the OC contract is the highest compared with the other contracts. Specifically, the retailer prefers increasing the product price as the streamer's effort increases. Third, the manufacturer offers a high wholesale price when the retailer cooperates with a high-ability streamer through the OC contract. However, the result is the opposite when the retailer cooperates with a low-ability streamer. This result possibly occurs because the manufacturer believes that a low-ability streamer cannot persuade more viewers to buy products during live streaming.
Effects of the three contracts: We reveal that: (1) the retailer is willing to sign the OC contract with a high-ability streamer, wherein the manufacturer can act as a “free rider.” In particular, when the fixed fee is small, the manufacturer, retailer, and high-ability streamer can achieve a win–win outcome through an OC contract. The retailer is willing to sign an OC contract with a low-ability streamer when the fixed fee of the OF contract is high. (2) The retailer is willing (reluctant) to cooperate with a low-ability streamer through an OF contract when the fixed fee is low (high). When the fixed fee of the OF contract is low, the retailer need not bear the high costs of employing a streamer. (3) The retailer prefers the CF contract when the total commission rate (i.e., \(\alpha +\beta\)) is small and the fixed fee (i.e., \(k\)) is medium.
This study exhibits some limitations. First, solving the product return problem in live streaming requires further research in the future. Second, cooperating with several streamers to promote products can be considered to examine the optimal contract strategy, which can provide more interesting and valuable insights.
Data availability
We did not analyze or generate any datasets because our work proceeds within a theoretical and mathematical framework.
Notes
Available at https://vantagedigital.com.au/ultimate-guide-taobao-live-streaming-17-lessons-from-top-5-streamers/. (Accessed 2021).
Available at https://chinamktginsights.com/paying-100k-rmb-to-sell-5-thermoses-how-to-avoid-a-celebrity-livestream-horror-story/. (Accessed 2021).
Wu, J., 2020. Businesses "hollowed out" by Sydney: they can't earn, they can't escape. https://car.inotgo.com/2021/12/202112252017199064.html. (Accessed 2022).
Available at https://lujuba.cc/en/632400.html. (Accessed 2022).
References
Avinadav, T. (2020). The effect of decision rights allocation on a supply chain of perishable products under a revenue-sharing contract. International Journal of Production Economics, 225, 107587.
Benitez, C (2021). The ultimate list of live streaming statistics for 2021. (August 6th). https://findstack.com/live-streaming-statistics/
Bart, N., Chernonog, T., & Avinadav, T. (2021). Revenue-sharing contracts in supply chains: A comprehensive literature review. International Journal of Production Research, 59(21), 6633–6658.
Cai, J., Hu, X., Tadikamalla, P. R., & Shang, J. (2017). Flexible contract design for VMI supply chain with service-sensitive demand: Revenue-sharing and supplier subsidy. European Journal of Operational Research, 261(1), 143–153.
Cao, E. (2014). Coordination of dual-channel supply chains under demand disruptions management decisions. International Journal of Production Research, 52(23), 7114–7131.
Chen, C.-C., & Lin, Y.-C. (2018). What drives live-stream usage intention? The perspectives of flow, entertainment, social interaction, and endorsement. Telematics and Informatics, 35(1), 293–303.
Chen, H., Zhang, S., Shao, B., Gao, W., & Xu, Y. (2021). How do interpersonal interaction factors affect buyers’ purchase intention in live stream shopping? Internet Research. https://doi.org/10.1108/INTR-05-2020-0252
Clement Addo, P., Fang, J., Asare, A. O., & Kulbo, N. B. (2021). Customer engagement and purchase intention in live-streaming digital marketing platforms. The Service Industries Journal, 41, 1–20.
Enron (2020). The sales of 1.2 million pit fees are less than half. Is the live broadcast of selling courses really a loss-making business? http://www.ww01.net/en/archives/73811
Erjiang, E., Yu, M., & Peng, G. (2021). Intermediation in reward-based crowdfunding: A cash deposit mechanism to reduce moral hazard. Electronic Commerce Research, 33, 1–22.
Fatehi, S., & Wagner, M. R. (2019). Crowdfunding via revenue-sharing contracts. Manufacturing and Service Operations Management, 21(4), 875–893.
Gao, X., Xu, X. Y., Tayyab, S. M. U., & Li, Q. (2021). How the live streaming commerce viewers process the persuasive message: An ELM perspective and the moderating effect of mindfulness. Electronic Commerce Research and Applications, 49, 101087.
He, Y., Wang, H., Guo, Q., & Xu, Q. (2019). Coordination through cooperative advertising in a two-period consumer electronics supply chain. Journal of Retailing and Consumer Services, 50, 179–188.
He, Y., Xu, Q., & Shao, Z. (2021). ‘Ship-from-Store’ strategy in platform retailing. Transportation Research Part E: Logistics and Transportation Review, 145, 102153.
He, Y., Xu, Q., Xu, B., & Wu, P. (2016). Supply chain coordination in quality improvement with reference effects. Journal of the Operational Research Society, 67(9), 1158–1168.
Heydari, J., & Ghasemi, M. (2018). A revenue sharing contract for reverse supply chain coordination under stochastic quality of returned products and uncertain remanufacturing capacity. Journal of Cleaner Production, 197, 607–615.
Hu, M., & Chaudhry, S. S. (2020). Enhancing consumer engagement in e-commerce live streaming via relational bonds. Internet Research, 30(3), 1019–1041.
Hu, Y., Qu, S., Li, G., & Sethi, S. P. (2021). Power structure and channel integration strategy for online retailers. European Journal of Operational Research, 294(3), 951–964.
Kang, K., Lu, J., Guo, L., & Li, W. (2021). The dynamic effect of interactivity on customer engagement behavior through tie strength: Evidence from live streaming commerce platforms. International Journal of Information Management, 56, 102251.
Kim, H. S., & Kim, M. (2021). Viewing sports online together? Psychological consequences on social live streaming service usage. Sport Management Review, 23(5), 869–882.
Kim, J., & Kim, M. (2020). Spectator e-sport and well-being through live streaming services. Technology in Society, 63, 101401.
Li, G., Tian, L., & Zheng, H. (2021). Information sharing in an online marketplace with co-opetitive sellers. Production and Operations Management, 30(10), 3713–3734.
Li, G., Wu, H., & Zheng, H. (2021). Technology investment strategy for a competitive manufacturer in the presence of technology spillover. IEEE Transactions on Engineering Management. https://doi.org/10.1109/TEM.2021b.3105014
Li, Q., Xiao, T., & Qiu, Y. (2018). Price and carbon emission reduction decisions and revenue-sharing contract considering fairness concerns. Journal of Cleaner Production, 190, 303–314.
Li, R., Lu, Y., Ma, J., & Wang, W. (2021). Examining gifting behavior on live streaming platforms: An identity-based motivation model. Information and Management, 58(6), 103406.
Linh, C. T., & Hong, Y. (2009). Channel coordination through a revenue sharing contract in a two-period newsboy problem. European Journal of Operational Research, 198(3), 822–829.
Liu, G., Yang, H., & Dai, R. (2020). Which contract is more effective in improving product greenness under different power structures: Revenue sharing or cost sharing? Computers and Industrial Engineering, 148, 106701.
Liu, H., & Liu, S. (2021). Optimal decisions and coordination of live streaming selling under revenue-sharing contracts. Managerial and Decision Economics, 42(4), 1022–1036.
Lu, B., & Chen, Z. (2021). Live streaming commerce and consumers’ purchase intention: An uncertainty reduction perspective. Information and Management, 58(7), 103509.
Lu, S., Yao, D., Chen, X., & Grewal, R. (2021). Do larger audiences generate greater revenues under pay what you want? Evidence from a live streaming platform. Marketing Science. https://doi.org/10.1287/mksc.2021.1292
Ma, Y. (2021). To shop or not: Understanding Chinese consumers’ live-stream shopping intentions from the perspectives of uses and gratifications, perceived network size, perceptions of digital celebrities, and shopping orientations. Telematics and Informatics, 59, 101562.
Mu, L., Tang, X., Sugumaran, V., Xu, W., & Sun, X. (2021). Optimal rebate strategy for an online retailer with a cashback platform: commission-driven or marketing-based? Electronic Commerce Research, 1–36. https://doi.org/10.1007/s10660-021-09485
Palsule-Desai, O. D. (2013). Supply chain coordination using revenue-dependent revenue sharing contracts. Omega, 41(4), 780–796.
Panja, S., & Mondal, S. K. (2020). Exploring a two-layer green supply chain game theoretic model with credit linked demand and mark-up under revenue sharing contract. Journal of Cleaner Production, 250, 119491.
Park, H. J., & Lin, L. M. (2020). The effects of match-ups on the consumer attitudes toward internet celebrities and their live streaming contents in the context of product endorsement. Journal of Retailing and Consumer Services, 52, 101934.
Song, H., & Gao, X. (2018). Green supply chain game model and analysis under revenue-sharing contract. Journal of Cleaner Production, 170, 183–192.
Sun, Y., Shao, X., Li, X., Guo, Y., & Nie, K. (2019). How live streaming influences purchase intentions in social commerce: An IT affordance perspective. Electronic Commerce Research and Applications, 37, 100886.
Tsao, Y.-C., & Lee, P.-L. (2020). Employing revenue sharing strategies when confronted with uncertain and promotion-sensitive demand. Computers and Industrial Engineering, 139, 106200.
Wang, X., Tao, Z., Liang, L., & Gou, Q. (2019). An analysis of salary mechanisms in the sharing economy: The interaction between streamers and unions. International Journal of Production Economics, 214, 106–124.
Wongkitrungrueng, A., & Assarut, N. (2020). The role of live streaming in building consumer trust and engagement with social commerce sellers. Journal of Business Research, 117, 543–556.
Wongkitrungrueng, A., Dehouche, N., & Assarut, N. (2020). Live streaming commerce from the sellers’ perspective: Implications for online relationship marketing. Journal of Marketing Management, 36(5–6), 488–518.
Xu, G., Dan, B., Zhang, X., & Liu, C. (2014). Coordinating a dual-channel supply chain with risk-averse under a two-way revenue sharing contract. International Journal of Production Economics, 147, 171–179.
Xu, Q., & He, Y. (2021). Optimal information disclosure strategies for a retail platform in the blockchain technology era. International Journal of Production Research. https://doi.org/10.1080/00207543.2021.1976434
Xu, X., Wu, J.-H., & Li, Q. (2020). What drives consumer shopping behavior in live streaming commerce? Journal of Electronic Commerce Research, 21(3), 144–167.
Yang, H., Luo, J., & Wang, H. (2017). The role of revenue sharing and first-mover advantage in emission abatement with carbon tax and consumer environmental awareness. International Journal of Production Economics, 193, 691–702.
Yan, R. (2008). Profit sharing and firm performance in the manufacturer-retailer dual-channel supply chain. Electronic Commerce Research, 8(3), 155–172.
Yu, E., Jung, C., Kim, H., & Jung, J. (2018). Impact of viewer engagement on gift-giving in live video streaming. Telematics and Informatics, 35(5), 1450–1460.
Zhang, J., & Chen, J. (2013). Coordination of information sharing in a supply chain. International Journal of Production Economics, 143(1), 178–187.
Zhao, D., Chen, M., & Gong, Y. (2019). Strategic information sharing under revenue-sharing contract: Explicit vs. tacit collusion in retailers. Computers and Industrial Engineering, 131, 99–114.
Acknowledgements
This work was supported by China's National Natural Science Foundation (Grant Number 71872075), Hainan Provincial Natural Science Foundation of China (Grant Number 720RC568) and Hainan Provincial Postgraduate Innovation Research Project (Grant Number Qhyb2021-18).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
On behalf of all the authors, the corresponding author states no conflicts of interest.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
1.1 Proof of equilibrium solutions in Table 2
Under model OC
The retailer’s profit under the OC contract is:
The first and second derivatives of \({\pi }_{r}^{OC}\) regarding \({p}^{OC}\) are \(\frac{d{\pi }_{r}^{OC}}{d{p}^{OC}}=b{e}^{OC}+r+{w}^{OC}-2{p}^{OC}+1\) and \(\frac{{d}^{2}{\pi }_{r}^{OC}}{d{p}^{{2}_{OC}}}=-2\), respectively.
Since \(\frac{{d}^{2}{\pi }_{r}^{OC}}{d{p}^{{2}_{OC}}}=-2<0\), the retailer’s profit under the OC contract is concave in \({p}^{OC}\).
The streamer’s profit under the OC contract is:
The first and second derivatives of \({\pi }_{s}^{OC}\) regarding \({e}^{OC}\) are \(\frac{d{\pi }_{s}^{OC}}{d{e}^{OC}}=br-c{e}^{OC}+s\) and \(\frac{{d}^{2}{\pi }_{s}^{OC}}{d{e}^{{2}_{OC}}}=-c\), respectively.
Since \(\frac{{d}^{2}{\pi }_{s}^{OC}}{d{e}^{{2}_{OC}}}=-c<0\), the streamer’s profit under the OC contract is concave in \({e}^{OC}\).
Thus, by solving \(\frac{d{\pi }_{r}^{OC}}{d{p}^{OC}}=0\) and \(\frac{d{\pi }_{s}^{OC}}{d{e}^{OC}}=0\) simultaneously, we have:
Through backward induction, we substitute \({p}^{OC}\) and \({e}^{OC}\) into the manufacturer’s profit—that is, \({\pi }_{m}^{OC}={w}^{OC}(1-{p}^{OC}+b{e}^{OC})\). We have \({\pi }_{m}^{OC}={w}^{OC}(b\left(br+s\right)/c-({b}^{2}r+bs+cr+c{w}^{OC}+c)/2c+1\).
The first and second derivatives of \({\pi }_{m}^{OC}\) with respect to \({w}^{OC}\) are \(\frac{d{\pi }_{m}^{OC}}{d{w}^{OC}}=b\left(br+s\right)/c-({b}^{2}r+bs+cr+c{w}^{OC}+c)/2c+1-{w}^{OC}/2\) and \(\frac{{d}^{2}{\pi }_{m}^{OC}}{d{w}^{{2}_{OC}}}=-1<0\), respectively.
Thus, by solving \(\frac{d{\pi }_{m}^{OC}}{d{w}^{OC}}=0\), we have \({w}^{OC*}=({b}^{2}r+bs-cr+c)/2c\). Next, we substitute \({w}^{OC*}\) with \({p}^{OC}=({b}^{2}r+bs+cr+c{w}^{OC}+c)/2c\). Thus, we obtain \({p}^{OC*}=(r+3)c+3{b}^{2}r+3bs/4c\).
Under model OF.
The retailer’s profit under the OF contract is:
The first and second derivatives of \({\pi }_{r}^{OF}\) regarding \({p}^{OF}\) are \(\frac{d{\pi }_{r}^{OF}}{d{p}^{OF}}=b{e}^{OF}+{w}^{OF}-2{p}^{OF}+1\) and \(\frac{{d}^{2}{\pi }_{r}^{OF}}{d{p}^{{2}_{OF}}}=-2\), respectively.
Since \(\frac{{d}^{2}{\pi }_{r}^{OF}}{d{p}^{{2}_{OF}}}=-2<0\), the retailer’s profit under the OF contract is concave in \({p}^{OF}\).
The streamer’s profit under the OF contract is:
The first and second derivatives of \({\pi }_{s}^{OF}\) regarding \({e}^{OF}\) are \(\frac{d{\pi }_{s}^{OF}}{d{e}^{OF}}=-c{e}^{OF}+s\) and \(\frac{{d}^{2}{\pi }_{s}^{OF}}{d{e}^{{2}_{OF}}}=-c\), respectively.
Since \(\frac{{d}^{2}{\pi }_{s}^{OF}}{d{e}^{{2}_{OF}}}=-c<0\), the streamer’s profit under OF contract is concave in \({e}^{OF}\).
Thus, by solving \(\frac{d{\pi }_{r}^{OF}}{d{p}^{OF}}=0\) and \(\frac{d{\pi }_{s}^{OF}}{d{e}^{OF}}=0\) simultaneously, we have:
Using backward induction, we substitute \({p}^{OF}\) and \({e}^{OF}\) into the manufacturer’s profit, that is, \({\pi }_{m}^{OF}={w}^{OF}(1-{p}^{OF}+b{e}^{OF})\). We obtain \({\pi }_{m}^{OF}={w}^{OF}\left(bs-c{w}^{OF}+c\right)/2c\).
The first and second derivatives of \({\pi }_{m}^{OF}\) regarding \({w}^{OF}\) are \(\frac{d{\pi }_{m}^{OF}}{d{w}^{OF}}=(bs-c{w}^{OF}+c)/2c-{w}^{OF}/2\) and \(\frac{{d}^{2}{\pi }_{m}^{OF}}{d{w}^{{2}_{OF}}}=-1<0\), respectively.
Thus, by solving \(\frac{d{\pi }_{m}^{OF}}{d{w}^{OF}}=0\), we have \({w}^{OF}=(bs+c)/2c\). Next, we substitute \({w}^{OF*}\) into \({p}^{OF}=(bs+c{w}^{OF}+c)/2c\). Thus, we can obtain \({p}^{OF*}=(3c+3bs)/4c\).
Under model CF.
The retailer’s profit under the CF contract is:
The first and second derivatives of \({\pi }_{r}^{CF}\) regarding \({p}^{CF}\) are \(\frac{d{\pi }_{r}^{CF}}{d{p}^{CF}}=b{e}^{CF}+\beta r+{w}^{CF}-2{p}^{CF}+1\) and \(\frac{{d}^{2}{\pi }_{r}^{CF}}{d{p}^{{2}_{CF}}}=-2\), respectively.
Since \(\frac{{d}^{2}{\pi }_{r}^{CF}}{d{p}^{{2}_{CF}}}=-2<0\), the retailer’s profit under the CF contract is concave in \({p}^{CF}\).
The streamer’s profit under the CF contract is:
The first and second derivatives of \({\pi }_{s}^{CF}\) regarding \({e}^{CF}\) are \(\frac{d{\pi }_{s}^{CF}}{d{e}^{CF}}=b\beta r-c{e}^{OF}+s\) and \(\frac{{d}^{2}{\pi }_{s}^{CF}}{d{e}^{{2}_{CF}}}=-c\), respectively.
Since \(\frac{{d}^{2}{\pi }_{s}^{CF}}{d{e}^{{2}_{CF}}}=-c<0\), the streamer’s profit under the CF contract is concave in \({e}^{CF}\).
Thus, by solving \(\frac{d{\pi }_{r}^{CF}}{d{p}^{CF}}=0\) and \(\frac{d{\pi }_{s}^{CF}}{d{e}^{CF}}=0\) simultaneously, we have:
Using backward induction, we substitute \({p}^{CF}\) and \({e}^{CF}\) into the manufacturer’s profit—that is, \({\pi }_{m}^{CF}={w}^{CF}(1-{p}^{CF}+b{e}^{CF})\). We have \({\pi }_{m}^{CF}={w}^{CF}(b\left(b\beta r+s\right)/c-({b}^{2}\beta r+\beta cr+bs+c{w}^{CF}+c)/2c+1\).
The first and second derivatives of \({\pi }_{m}^{CF}\) for \({w}^{CF}\) are \(\frac{d{\pi }_{m}^{CF}}{d{w}^{CF}}=b\left(b\beta r+s\right)/c-({b}^{2}\beta r+\beta cr+bs+c{w}^{CF}+c)/2c+1-{w}^{CF}/2\) and \(\frac{{d}^{2}{\pi }_{m}^{CF}}{d{w}^{{2}_{CF}}}=-1<0\), respectively.
Thus, by solving \(\frac{d{\pi }_{m}^{CF}}{d{w}^{OF}}=0\), we obtain \({w}^{CF}=(r({b}^{2}-c)\beta +bs+c)/2c\). Next, we substitute \({w}^{CF*}\) with \({p}^{CF}=\left({b}^{2}\beta r+\beta cr+bs+c{w}^{OF}+c\right)/2c\). Thus, we obtain \({p}^{CF*}=(\beta r+3)c+3{b}^{2}\beta r+3bs)/4c\).
1.2 Proof of proposition 1
In accordance with the optimal streamer’s effort, we list the wholesale and product prices under different contracts in Table 2.
Since \({e}^{CF*}-{e}^{OF*}=b\beta r/c>0\) and \({e}^{OC*}-{e}^{CF*}=b\left(1-\beta \right)r/c>0\), we can directly derive, \({e}^{CF*}>{e}^{OF*}\) and \({e}^{OC*}>{e}^{CF*}\). Thus, \({e}^{OF*}<{e}^{CF*}<{e}^{OC*}\).
Since \({p}^{CF*}-{p}^{OF*}=(c\beta r+3{b}^{2}\beta r)/4c>0\) and \({p}^{OC*}-{p}^{CF*}=(r\left(1-\beta \right)c+3{b}^{2}(1-\beta )r)/4c>0\), we can directly derive, \({p}^{CF*}>{p}^{OF*}\) and \({p}^{OC*}>{p}^{CF*}\). Therefore, \({p}^{OF*}<{p}^{CF*}<{p}^{OC*}\).
As before, considering \({w}^{OF*}-{w}^{CF*}=r(c-{b}^{2})\beta /2c\), if \(c<{b}^{2}\), we have \({w}^{OF*}-{w}^{CF*}<0\); otherwise, \({w}^{OF*}-{w}^{CF*}>0\).
Considering \({w}^{OF*}-{w}^{OC*}=r(c-{b}^{2})/2c\), if \(c<{b}^{2}\), we have \({w}^{OF*}-{w}^{OC*}<0\); otherwise, \({w}^{OF*}-{w}^{OC*}>0\).
Considering \({w}^{CF*}-{w}^{OC*}=r\left(1-\beta \right)(c-{b}^{2})/2c\), if \(c<{b}^{2}\), we have \({w}^{CF*}-{w}^{OC*}<0\); otherwise, \({w}^{CF*}-{w}^{OC*}>0\).
To summarize, given that \(c<{b}^{2}\), we have \({w}^{OF*}<{w}^{CF*}<{w}^{OC*}\); otherwise, we have \({w}^{OF*}>{w}^{CF*}>{w}^{OC*}\).
1.3 Proof of proposition 2
Considering \({D}^{OF*}-{D}^{CF*}=r(c-{b}^{2})\beta /4c\), if \(c<{b}^{2}\), we have \({D}^{OF*}-{D}^{CF*}<0\); otherwise, \({D}^{OF*}-{D}^{CF*}>0\).
Considering \({D}^{OF*}-{D}^{OC*}=r(c-{b}^{2})/4c\), if \(c<{b}^{2}\), we have \({D}^{OF*}-{D}^{OC*}<0\); otherwise, \({D}^{OF*}-{D}^{OC*}>0\).
Considering \({D}^{CF*}-{D}^{OC*}=r\left(1-\beta \right)(c-{b}^{2})/4c\), if \(c<{b}^{2}\), we have \({D}^{CF*}-{D}^{OC*}<0\); otherwise, \({D}^{CF*}-{D}^{OC*}>0\).
To summarize, given that \(c<{b}^{2}\), we have \({D}^{CF*}<{D}^{CF*}<{D}^{OC*}\); otherwise, we have \({D}^{CF*}>{D}^{CF*}>{D}^{OC*}\).
1.4 Proof of proposition 3
Let \({k}_{OF-OC}\) denote the fixed-fee cut-off point for the retailer under OF and OC contracts. We set \({\pi }_{r}^{OF*}-{\pi }_{r}^{OC*}=0\) to derive \({k}_{OF-OC}=\left(\left({b}^{2}r+2bs-c\left(r-2\right)\right)\left(c-{b}^{2}\right)r\right)/16{c}^{2}\). If \(k<{k}_{OF-OC}\), we have \({\pi }_{r}^{OF*}>{\pi }_{r}^{OC*}\); otherwise, we have \({\pi }_{r}^{OF*}<{\pi }_{r}^{OC*}\).
Let \({k}_{CF-OF}\) denote the fixed fee cut-off point for the retailer under CF and OF contracts. We set \({\pi }_{r}^{CF*}-{\pi }_{r}^{OC*}=0\) to derive \({k}_{CF-OF}=\left(\left(r\left({b}^{2}-c\right)\beta +2bs+2c\right)\beta \left(c-{b}^{2}\right)r\right)/16{c}^{2}\left(1-\alpha \right)\). If \(k>{k}_{CF-OF}\), we have \({\pi }_{r}^{CF*}>{\pi }_{r}^{OF*}\); otherwise, we have \({\pi }_{r}^{CF*}<{\pi }_{r}^{OF*}\).
Let \({k}_{CF-OR}\) denote the fixed-fee cut-off point for the retailer under CF and OC contracts. We set \({\pi }_{r}^{CF*}-{\pi }_{r}^{OC*}=0\) to derive \({k}_{CF-OC}=((\left(-r\beta -r+2\right)c+\left(r\left(\beta +1\right)b+2s\right)b)\left(1-\beta \right)\left(c-{b}^{2}\right)r)/16{c}^{2}\). If \(k<{k}_{CF-OC}\), we have \({\pi }_{r}^{CF*}>{\pi }_{r}^{OC*}\); otherwise, we have \({\pi }_{r}^{CF*}<{\pi }_{r}^{OC*}\).
When \(c<{b}^{2}\), we have \({k}_{OF-OC}=\left(\left({b}^{2}r+2bs-c\left(r-2\right)\right)\left(c-{b}^{2}\right)r\right)/16{c}^{2}<0\), \({k}_{CF-OF}=\left(\left(r\left({b}^{2}-c\right)\beta +2bs+2c\right)\beta \left(c-{b}^{2}\right)r\right)/16{c}^{2}\left(1-\alpha \right)<0\), and \({k}_{CF-OC}=((\left(-r\beta -r+2\right)c+\left(r\left(\beta +1\right)b+2s\right)b)\left(1-\beta \right)\left(c-{b}^{2}\right)r)/16{c}^{2}<0\). Since the fixed fee is positive, we can derive \(\forall k>0>{k}_{OF-OC}\) \(\forall k>0>{k}_{CF-OF}\) And \(\forall k>0>{k}_{CF-OR}\). Thus, when \(c<{b}^{2}\), we can derive \({\pi }_{r}^{OC*}>{\pi }_{r}^{CF*}>{\pi }_{r}^{OF*}\).
For \(c-{b}^{2}>0\). To study the effects of the commission of sale \(r\) and fixed fee \(k\) on the retailer’s profit, we set \({k}_{CF-OF}-{k}_{CF-OC}=0\), \({k}_{OF-OC}-{k}_{CF-OF}=0\), and \({k}_{CF-OC}-{k}_{CF-OF}=0\), respectively. For any formula, we can obtain two roots for \(r\)—\({r}_{0}=0\) and \({r}_{1}=2\left(\beta +\alpha -1\right)\left(bs+c\right)/\left(\left({\beta }^{2}+\alpha -1\right)\left(c-{b}^{2}\right)\right)\). On the one hand, if \(\beta +\alpha -1>0\) and \({\beta }^{2}+\alpha -1>0\), we have \({r}_{1}>1\). The second derivative of \({k}_{RF-OF}-{k}_{RF-OR}\) with respect to \(r\) is \({\partial }^{2}\left({k}_{CF-OF}-{k}_{CF-OC}\right)/\partial {r}^{2}=\left({\beta }^{2}+\alpha -1\right){\left({b}^{2}-c\right)}^{2}/\left(16\alpha {c}^{2}\left(1-\alpha \right)\right)>0\). We can derive that \({k}_{CF-OF}>{k}_{CF-OC}\). \({\pi }_{r}^{CF}>max {(\pi }_{r}^{OF},{\pi }_{r}^{OC})\) only if \({k}_{CF-OF}<k<{k}_{CF-OC}\). Any \(k\) cannot satisfy the range; therefore, we can derive \({\pi }_{r}^{CF}<max {(\pi }_{r}^{OF},{\pi }_{r}^{OC})\).
On the other hand, we set \(\beta +\alpha -1>0\) and \({\beta }^{2}+\alpha -1<0\) to derive \({r}_{1}<0\) and \({\partial }^{2}\left({k}_{CF-OF}-{k}_{CF-OC}\right)/\partial {r}^{2}=\left({\beta }^{2}+\alpha -1\right){\left({b}^{2}-c\right)}^{2}/\left(16\alpha {c}^{2}\left(1-\alpha \right)\right)<0\); we also derive \({\pi }_{r}^{CF}<max {(\pi }_{r}^{OF},{\pi }_{r}^{OC})\). Therefore, when \(c-{b}^{2}>0\) and \(\beta +\alpha -1>0\), we have \({\pi }_{r}^{CF}<max {(\pi }_{r}^{OF},{\pi }_{r}^{OC})\).
If \(\beta +\alpha -1<0\) and \(\beta \in (\mathrm{0,1})\), \({\beta }^{2}+\alpha -1<0\); we have \({r}_{1}>1\) \({\partial }^{2}\left({k}_{CF-OC}-{k}_{OF-OC}\right)/\partial {r}^{2}=\left({\beta }^{2}+\alpha -1\right){\left({b}^{2}-c\right)}^{2}/\left(16\alpha {c}^{2}\right)<0\); we can derive that \({\pi }_{r}^{OC}\) outperforms both \({\pi }_{r}^{CF}\) and \({\pi }_{r}^{OF}\), if \(k>{k}_{CF-OC}\). Similarly, propositions 1(iii), (b), and (c) can be proved.
1.5 Proof of proposition 4
Let \({k}_{OF-OC}^{^{\prime}}\) denote the fixed fee cut-off point for the streamer under OF and OC contracts. We set \({\pi }_{s}^{OF*}-{\pi }_{s}^{OC*}=0\) to obtain \({k}_{OF-OC}^{^{\prime}}=r\left(-{b}^{2}r+bs-cr+c\right)/(4c)\). If \(k>{k}_{OF-OC}^{^{\prime}}\), we have \({\pi }_{s}^{OF*}>{\pi }_{s}^{OC*}\); otherwise, we have \({\pi }_{s}^{OF*}<{\pi }_{s}^{OC*}\).
Let \({k}_{CF-OF}^{^{\prime}}\) denote the fixed fee cut-off point for the retailer under CF and OF contracts. We set \({\pi }_{s}^{CF*}-{\pi }_{s}^{OF*}=0\) to obtain \({k}_{CF-OF}^{^{\prime}}=\beta r\left(-r\left({b}^{2}+c\right)\beta +bs+c\right)/\left(4c(1-\alpha )\right)\). If \(k<{k}_{CF-OF}^{^{\prime}}\), we have \({\pi }_{s}^{CF*}>{\pi }_{s}^{OF*}\); otherwise, we have \({\pi }_{s}^{CF*}<{\pi }_{s}^{OF*}\).
Let \({k}_{CF-OC}^{^{\prime}}\) denote the fixed-fee cut-off point for the retailer under CF and OC contracts. We set \({\pi }_{s}^{CF*}-{\pi }_{s}^{OC*}=0\) to obtain \({k}_{CF-OC}^{^{\prime}}=(1-\beta )r\left(-r\left({b}^{2}+c\right)(\beta +1)+bs+c\right)/4c\alpha\). If \(k>{k}_{CF-OC}^{^{\prime}}\), we have \({\pi }_{s}^{CF*}>{\pi }_{s}^{OC*}\); otherwise, we have \({\pi }_{s}^{CF*}<{\pi }_{s}^{OC*}\).
To study the effects of the commission of sale \(r\) and fixed fee \(k\) on the streamer’s profit, we set \({k}_{OF-OC}^{^{\prime}}-{k}_{CF-OC}^{^{\prime}}=0\); \({k}_{OF-OC}^{^{\prime}}-{k}_{CF-OF}^{^{\prime}}=0\); and \({k}_{CF-OC}^{^{\prime}}-{k}_{CF-OF}^{^{\prime}}=0\), respectively. For any formula, we can obtain two roots for \(r\)—\({r}_{0}=0\) and \({r}_{2}=(\beta +\alpha -1)\left(bs+c\right)/(({\beta }^{2}+\alpha -1)({b}^{2}+c))\). For \(\beta +\alpha -1>0\) and \({\beta }^{2}+\alpha -1>0\), we have \({r}_{2}>0\). The second derivative of \({k}_{CF-OC}^{^{\prime}}-{k}_{CF-OF}^{^{\prime}}\) with respect to \(r\) is \({\partial }^{2}\left({k}_{CF-OC}^{^{\prime}}-{k}_{CF-OF}^{^{\prime}}\right)/\partial {r}^{2}=\left({\beta }^{2}+\alpha -1\right)({b}^{2}+c)/\left(4\alpha c(\alpha -1)\right)<0\). Using the same method, the streamer’s profit relationship is that \({\pi }_{s}^{OR}>({\pi }_{s}^{RF}, {\pi }_{s}^{OF})\), if \(k<{k}_{CF-OC}^{^{\prime}}<{k}_{OF-OC}^{^{\prime}}\); if \(k>{k}_{CF-OF}^{^{\prime}}\), \({\pi }_{s}^{OF}>{(\pi }_{s}^{CF}, {\pi }_{s}^{OC})\); if \({k}_{CF-OC}^{^{\prime}}<k<{k}_{CF-OF}^{^{\prime}}\), \({\pi }_{s}^{CF}>({\pi }_{s}^{OF}, {\pi }_{s}^{OC})\).
If \(\beta +\alpha -1<0\) and \(\beta \in (\mathrm{0,1})\), \({\beta }^{2}+\alpha -1<0\). Under this condition, if \({r}_{2}>1\), i.e., \(s>{s}_{1}\), we have \({\partial }^{2}\left({k}_{CF-OC}^{^{\prime}}-{k}_{CF-OF}^{^{\prime}}\right)/\partial {r}^{2}=\left({\beta }^{2}+\alpha -1\right)({b}^{2}+c)/\left(4\alpha c(\alpha -1)\right)>0\). Consequently, \({k}_{CF-OF}<{k}_{CF-OC}\), which cannot satisfy \({k}_{CF-OC}<k<{k}_{CF-OF}\). Hence, \({\pi }_{r}^{CF}<max {(\pi }_{r}^{OF},{\pi }_{r}^{OC})\); furthermore, against this background, if \({r}_{2}<r<1\) and \(0<{r}_{2}<1\), i.e., \(0<s<{s}_{1}\), we have the same result as proposition 2(i). If \(0<r<{r}_{2}\) and \(0<{r}_{2}<1\), we can derive \({k}_{CF-OF}<{k}_{CF-OC}\).
1.6 Proof of proposition 5
Since \({\pi }_{m}^{OF*}-{\pi }_{m}^{OC*}=(2bs+{b}^{2}r+(2-r)c)(c-{b}^{2})r/8{c}^{2}\), if \(c-{b}^{2}>0\), we have \({\pi }_{m}^{OF*}>{\pi }_{m}^{OC*}\); otherwise, \({\pi }_{m}^{OF*}<{\pi }_{m}^{OC*}\).
Since \({\pi }_{m}^{OF*}-{\pi }_{m}^{CF*}=(2bs+{b}^{2}r\beta +(2-r\beta )c)(c-{b}^{2})r\beta /8{c}^{2}\), if \(c-{b}^{2}>0\), we have \({\pi }_{m}^{OF*}>{\pi }_{m}^{CF*}\); otherwise, \({\pi }_{m}^{OF*}<{\pi }_{m}^{CF*}\).
Let \({\pi }_{m}^{CF*}-{\pi }_{m}^{OC*}=(c-{b}^{2})r(1-\beta )(2bs+{b}^{2}r(\beta +1)+(2-r(\beta +1))c)/8{c}^{2}\); if \(c-{b}^{2}>0\), we derive that \({\pi }_{m}^{CF*}>{\pi }_{m}^{OC*}\); otherwise, \({\pi }_{m}^{CF*}<{\pi }_{m}^{OC*}\).
Therefore, if \(c-{b}^{2}>0\), we have \({\pi }_{m}^{OF*}>{\pi }_{m}^{CF*}>{\pi }_{m}^{OC*}\); otherwise, \({\pi }_{m}^{OF*}<{\pi }_{m}^{CF*}<{\pi }_{m}^{OC*}\).
Rights and permissions
About this article
Cite this article
He, Y., Chen, L., Mu, J. et al. Optimal contract design for live streaming shopping in a manufacturer–retailer–streamer supply chain. Electron Commer Res 24, 1071–1093 (2024). https://doi.org/10.1007/s10660-022-09591-3
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10660-022-09591-3