Abstract
In this study, loss estimation models were developed for reasonably accurate assessment of economic and human losses from seismic events in the Mediterranean region, based on damage assessment at an urban scale. Data were compiled from existing worldwide databases, and completed with earthquake information from regional studies. Economic data were converted to a single common currency unit (2015 USD value) and the wealth of the areas affected by 65 earthquakes of the region from 1900 to 2015 was assessed. Reduced-form models were used to determine economic and human losses, with earthquake magnitude and intensity as hazard-related variables, and gross domestic product of the affected area and the affected population as exposure-related variables. Damage to buildings was also used as a hazard-related variable to predict economic and human losses. Finally, site-specific regression models were proposed for economic and human losses due to earthquakes in the Mediterranean region, and more specifically, in Algeria. We show that by introducing the damage variable into the models, prediction error can be reduced, and that accuracy of loss model estimation is site dependent and requires regional data on earthquake losses to improve. A case study for Constantine, Algeria shows the improvements needed for increased accuracy.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Modeling the economic consequences of natural hazard-induced disasters has gained importance in recent years. In the Mediterranean region, earthquakes are one of the most critical natural hazards, and they can cause considerable economic and social losses. Coupled with the vulnerability of buildings and high social and economic exposure, earthquakes are a regular and serious threat to communities, particularly in Greece, Italy, Turkey, Morocco, and Algeria.
Between 1900 and 2015, the Mediterranean region experienced thousands of damaging earthquakes, some of which were major disasters, such as the earthquakes of Messina, Italy, in 1908 (Barbano et al. 2005), Chios-Cesme, Greece, in 1949 (Altinok et al. 2005), Agadir, Morocco, in 1960 (El Alami et al. 2004), El-Asnam, Algeria, in 1980 (Bertero and Shah 1983), Izmit, Turkey, in 1999 (Barka 1999), and more recently, Boumerdes, Algeria, in 2003 (Laouami et al. 2006). These six damaging earthquakes resulted in over 150,000 deaths and caused direct losses of more than USD 26.5 billion.
Magnitude and distance are the two key parameters that control the impact of an earthquake in an urbanized area. From 1900 to 2015, even moderate earthquakes (for example, the Agadir, Morocco, M 5.7 earthquake in 1960) have caused considerable economic loss and numerous fatalities, due to the vulnerability of traditional building stock. Although the number of potentially damaging earthquakes per year has neither increased nor decreased in recent decades, the vulnerability and exposure of communities have changed. According to the World Health Organization (WHO 2016), the urban population will continue to grow by approximately 1.5–1.6% per year from 2015 to 2030. As a result, about 2.8 million causalities due to earthquakes can be expected worldwide by 2100 (Holzer and Savage 2013). Because of the long return periods of the largest and most severe consequence earthquakes, and because few urban areas have yet to suffer such major events in their current configuration, Jackson (2006) noted that the greatest earthquake disasters appear to lie in the future.
The benefits of natural hazard mitigation programs have been fully recognized (Benson and Twigg 2004; Whitehead and Rose 2009), and earthquake loss models can provide relevant information for decision makers and policymakers (Guéguen et al. 2016). Moreover, the benefits of rapid and effective economic and human loss estimation modeling can be of utmost importance in the immediate aftermath of earthquake disasters (Erdik et al. 2011; Jaiswal and Wald 2013). Developing relevant earthquake loss models is challenging, because most economic and human loss models are based on post-earthquake interpretations, and the empirical relationships are derived from field observations that include substantial uncertainties (Brookshire et al. 1997). Before developing our earthquake loss models, the key questions that had to be addressed were: (1) how to represent the losses from the wealth of the region via a macroeconomic indicator; (2) how to express the economic losses by a homogeneous monetary value over the period of the earthquakes; (3) how to express the magnitude of the seismic hazard; and (4) which functional form of the loss model needed to be used?
There are various models in the literature for rapid assessment of earthquake losses based on economic and human predictors, such as gross domestic product (GDP) and population (Chen et al. 1997; Cha 1998; Chen et al. 2001; Dunbar et al. 2002; Heatwole and Rose 2013). Most of the models are reduced-form models, which consider only one or two parameters. Using a theoretical model, Schumacher and Strobl (2011) showed that economic loss (per capita) due to disasters increases with the size and density of the population in the affected area, and that GDP per capita and its squared value can show statistical significance for loss models. Chen et al. (1997) proposed a model for losses as a function of the occurrence probability of the intensity and a vulnerability function derived empirically by correlating reported losses from past earthquakes with the GDP of the affected area. Using only 29 earthquakes, Cha (1998) developed a log–log relationship between economic losses and GDP for each intensity. Heatwole and Rose (2013) proposed a specific reduced-form model based on U.S. earthquakes that considered a linear regression model of predictor variables to predict losses. Their study examined the population of the affected area, the magnitude of the earthquake, and the total economic losses adjusted to 2011 values using the Consumer Price Index. Jaiswal et al. (2011) published a worldwide model to predict economic impacts for any earthquake. They examined earthquakes that occurred between 1980 and 2007 in 119 countries through a combination of seismic intensity, spatial distribution of the population, and total GDP, as scaled using an exposure correction factor—ratio of wealth per capita to GDP per capita. The wealth estimate per capita was adjusted to the year 2000 value using values derived from the World Bank website.Footnote 1
Based on the observation that economic and social losses are generally related to physical damage caused to buildings (D’Ayala et al. 1997; Bommer et al. 2002; Coburn and Spence 2002; So and Spence 2013), models require a detailed inventory of buildings. Several such models have been developed to forecast socioeconomic losses; for example, the U.S. Federal Emergency Management Agency (FEMA) methodology (HAZUS) for the estimation of potential losses from disasters (FEMA 2016), and the Norwegian Seismic Array (NORSAR) methodology of seismic loss estimation (SELENA) that uses a logic tree approach (Molina et al. 2010). For these models, economic losses and casualties were computed based on building vulnerability and damage for a given seismic hazard. The requirement for a detailed building inventory can be a major drawback for extending loss models to specific areas because of the sheer number of different buildings and the complications involved in accurately assessing their seismic resistance (Guéguen 2013). But recent studies have shown the efficiency of data mining-based vulnerability assessment methods on a large scale that use elementary building characteristics, such as the number of floors and the roof shape. These structural features can easily be assessed by remote sensing or are contained in national databases (Riedel et al. 2014, 2015).
There are relatively few studies on human casualties in the literature. Samardjieva and Oike (1992), Samardjieva and Badal (2002), and Badal et al. (2005) analyzed and tested a model to estimate the (log value of the) number of casualties as a function of the magnitude and population density for earthquakes worldwide. Nichols and Beavers (2003) established a simple equation between fatalities and magnitude for U.S. earthquakes. Jaiswal and Wald (2010) developed a specific empirical model for estimation of earthquake fatalities based on the shaking intensity and the number of people exposed to earthquakes recorded between 1973 and 2007. Post-earthquake observations consistently show that there is strong correlation between fatalities and damage to buildings. After the Armenian earthquake in 1988, Armenian et al. (1997) reported that being inside a building at the time of the earthquake was the most efficient predictor for fatality, which was related to the damage grade. Coburn and Spence (2002) developed an empirical fatality model that considers the European Macro Scale damage grade (EMS98) as a predictor variable (that is, D4 for extensive damage and D5 for total collapse).
A consensus emerges with regard to the importance of building damage as a contributing factor for losses and the need to consider regional models based on regional earthquake data. Since it appears that losses are directly related to the amount of damage, construction quality will be a key factor, which requires limiting the model to a specific region wherein the structural design is comparable. Moreover, in our dataset, many moderate earthquakes—for example, the 1960 Agadir earthquake—caused significant economic and human losses associated with severe building damage. Consequently, earthquake characteristics—for example, magnitude, intensity—alone are not sufficient to derive earthquake loss models. Moreover, to help earthquake crisis management and the prediction of the recovery period, the number of people who lost their homes is another key piece of information.
The main objective of this study is to consider damage as a hazard-related parameter and to show improvement in the accuracy of loss estimation obtained in empirical models by using this parameter instead of intensity and/or magnitude alone as hazard-related parameters. We developed empirical models for economic losses and human losses (home loss, injuries, fatalities) from earthquakes as applied to the Mediterranean region through the compilation of data from different databases and countries. Particular attention has been paid to Algeria—a high exposure, seismic-prone region—to show the benefit of reducing uncertainties by considering regional events for loss models. Several models and exposure variables were also tested (population, GDP). In the following section, we present the data on seismological features (magnitude, location) and economic, social, and physical consequences. When the regression models are developed, the results and their interpretations are discussed. Finally, these models are applied to a case study of Constantine, Algeria using data from a large-scale vulnerability assessment that was carried out previously using data mining-based methods.
2 Mediterranean Earthquakes and Losses Data
To develop a seismic loss model for a specific region with any degree of reliability, historical data of earthquake impact must be carefully considered and compiled in a comprehensive way. This involves the review of existing earthquake catalogs, engineering damage reports, and databases of losses reported after earthquakes, among other sources. The objective of the present study was not to offer a comparative analysis of data quality, and the selection of the data sources here was based on their international use and dissemination, or considered as being authoritative at the national scale. For this study, hundreds of reports and publications were consulted, but only a few reports that described losses in detail were ultimately used.
The region considered is the Mediterranean region (Fig. 1), which includes several earthquake-prone countries and is exposed to both strong (for example, Italy, Algeria, Greece) and moderate (for example, France, Morocco, Libya) seismic hazard. The data are drawn from the period of 1900–2015, and are for earthquakes for which detailed loss reports were available. Following a scientific approach, only accessible, public documents were considered, and these are referenced to allow the traceability of the information used.
The characteristics of the earthquakes are given in Tables 1 and 2. Magnitude and intensity (the Mercalli modified intensity) are from the U.S. Geological Survey earthquake search catalogFootnote 2 for earthquakes after 1980, and from public reports or peer-reviewed articles for others. As an example, Benouar (1994) completed a database of the strongest Algerian earthquakes for the 1900–1980 period, the Algerian Technical Office (Azzouz 2002; Azzouz and Rebzani 2005) provided information on specific earthquakes, and on behalf of the French ministry in charge of natural disaster management, Payany (1983) provided information on the damaging earthquakes that occurred in France in 1909. The final dataset consisted of 65 earthquakes that occurred between 1908 and 2014, with maximal epicentral intensities ≥ VI (Table 1), and located in nine countries: Algeria (24), Italy (12), Greece (11), Turkey (11), Morocco (2), Spain (2), France, Libya, and Egypt (1 each). Figure 2a shows the distribution of the earthquakes per country. This study does not include all the damaging earthquakes in the Mediterranean region over this period, mainly because either no data or only data from largely uncertain sources were available for some in terms of economic and human losses.
The Earthquake Engineering Research Institute (EERI) reports (EERI 1986, 1992, 1995, 1998, 1999, 2004, 2012) provided a lot of post-earthquake descriptions that were collected in the field soon after the events, and these were used to complete the seismological information in our study. In terms of damage and economic and human losses, the EERI reports are often limited to information available immediately after the event. Several months, or even years, can pass after an earthquake before this information can be considered to be comprehensive, and definitive missing information on total socioeconomic losses is never updated in these reports. Additional official databases were therefore examined to gather the missing information for this study: the International Disaster Database EM-DAT (Guha-Sapir et al. 2016), the Damaging Earthquakes Database CATDAT (Daniell et al. 2011; CATDAT 2016), and the Significant Earthquake Database of the National Geophysical Datacenter (NGDC 2016). In these databases, no information was available on the reliability and accuracy of the data that they contained, related to, for instance, the exposed populations, economic losses, and fatalities, as these databases consisted only of compilations of reports.
The EM-DAT database was created in 1998 and is maintained by the Centre for Research on the Epidemiology of Disasters in Brussels, Belgium. This database contains comprehensive data related to the occurrence and effects of over 18,000 natural disasters throughout the world, from 1900 until the present day. The EM-DAT data were cross-checked with other sources of information, such as UN agencies, nongovernmental organizations, and reinsurance companies. The NGDC database that was developed by the National Center for Environmental Information is similar to EM-DAT. It contains data on over 5700 destructive earthquakes from 2150 B.C. to the present, including information related to socioeconomic losses. CATDAT was created in 2010, and it contains over 20,000 sources of information that provide data on losses from over 12,000 historical damaging earthquakes (Daniell et al. 2011). In the present study, we considered information from CATDAT for earthquakes that occurred between 2011 and 2014. Finally, additional sources of information, such as public and official reports and peer-reviewed articles completed the loss databases used in this study (Table 2). Figure 2b–d shows the distribution of the earthquakes considered in the present study for each data source, in terms of economic losses (Fig. 2b), home loss (Fig. 2c), and number of damaged buildings (Fig. 2d).
The earthquakes were mainly located in the most seismically active countries of the Mediterranean region (Italy, Greece, Turkey, and Algeria), which represent 90% of the dataset. As particular attention was given to the Algerian region in the present study, 37% of the selected earthquakes were in Algeria. This proportion is not representative of the seismicity rate over this period, but is due to the information that was available to the authors. As shown in Fig. 2, more than 60% of the data for socioeconomic losses was drawn from the EM-DAT (Guha-Sapir et al. 2016) and NGDC (2016) databases. Because our objective was to construct the most comprehensive and traceable dataset possible, the data sources were cross-referenced according to their international audience or dissemination and validation at the international level, and references for the preferred source of information for earthquake occurrence were included in Tables 1 and 2.
3 Method
Based on data from the Mediterranean earthquake and loss database developed for this study, and using regression analysis between economic and human losses and hazard and exposure factors, empirical loss models for earthquakes in the Mediterranean region are developed in this study and their accuracy is examined. These models are then applied in a case study of Algeria for earthquake loss prediction. As a first step to develop empirical seismic loss models from the predictor variables available in the study database, the regression model forms proposed by Cha (1998) for GDP and seismic intensities, Heatwole and Rose (2013) for magnitude, population, and GDP, and Samardjieva and Badal (2002) for population and magnitude are adopted in this study.
Economic losses (L) are considered as a key dependent variable of the regression models. Daniell et al. (2010) reported that economic losses not adjusted to current USD values are a significant difficulty when compiling earthquake data from different epochs. To compare the consequences of earthquakes in a comprehensive manner, the actual economic losses were adjusted and normalized to a common and unique value (Daniell et al. 2011)—the 2015 USD currency. Nevertheless, for many countries around the Mediterranean (for example, France, Algeria, and Italy), this value was only available from the national census agencies after 1950, and GDP data before 1950 was provided by Maddison (2006). Inflation was allowed for, with the use of the Consumer Price Index inflation calculator from the Bureau of Labor Statistics, U.S. Department of LaborFootnote 3 to update the economic loss value adjusted from the year of the earthquake (L EQ ) to the present-day value (L $2015). For the Algerian earthquakes and the single French earthquake of Lambesc (1909), L EQ was given in currencies that no longer exist. Here, the French Institute of Statistics and Economic Studies converterFootnote 4 was used to convert L EQ into current currency in Euros on the date of the earthquake, which was then adjusted to the L $2015 (Table 2).
Home loss (H), injury (I), and fatality (F) are used as dependent variables of the regression models for human (social) losses, and their statistics came directly from the EM-DAT and NGDC databases for most of the earthquakes considered in the present study, or from referenced reports (Table 1).
Earthquake intensity and magnitude and building damage are selected as hazard variables. Damage (D) is usually reported as the total number of buildings that suffer damage. The present study determined the total number of buildings based on those having suffered heavy to strong damage, as classified by the damage grades D4 and D5 (Table 2), according to the EMS98 damage scale.
Population affected by the earthquakes (POP.Unit) is considered an important exposure variable, and these data came either from direct reports or other references (Table 2):
where A Aff is the size of the affected area, A Tot is the surface area, and POP Tot is the population of the country, on the date of the earthquake. POP Tot was provided by the Population City database,Footnote 5 taking into account the population growth rate. A Aff was obtained either from references or through estimation from seismic intensity maps.
GDP per capita on the date of the earthquake (GDP PC ), as another key exposure variable, is scaled by the population (POP.Unit), and GDP of the affected area (GDP.Unit) is then estimated by multiplying GDP PC by POP.Unit, as follows and is presented in Table 2:
The GDP values adjusted to the USD 2015 values were obtained from the World Bank website.Footnote 6 For Algeria before 1960, this information was provided by Clerc (1975).
Because of the lack of information, earthquake-induced losses were not distinguished between those directly caused by the earthquake and those due to tsunamis and/or fires that accompanied the Messina earthquake in 1908. Indeed, Bird and Bommer (2004) reported a small contribution of secondary events to the total losses (except for mega-earthquakes, such as Indonesia 2004 and Japan 2011, which were not in the present study).
4 Results
Empirical relationships between loss variables and hazard and exposure factors are presented in this section. The accuracy of the relationships derived from the database information is estimated using the standard error (RMSE), the coefficient of determination (R 2), and the adjusted R 2.
4.1 Economic Losses (L $2015) Versus GDP and Intensity
The linear regression model proposed by Cha (1998) that considers the GDP of the country on the date of the earthquake, is as follows:
where log10 indicates the decimal logarithmic function, a(MMI) and b(MMI) are the regression coefficients that depend on seismic intensity, ε is the RMSE, and L EQ and GDP are given in million USD.
In the Cha (1998) study, 29 earthquakes worldwide over the 1980–1995 period, of seismic intensities VIII, IX, and X were considered when deriving a loss empirical model. Figure 3 shows the log10 values of the losses in USD adjusted to the 2015 value (L $2015) versus the GDP.Unit predictor variable of the selected Mediterranean earthquakes and according to seismic intensities given in Table 1 and exposure-related variable in Table 2. Only 54 observations with VI < MMI < XI and with L $2015 and GDP.Unit information available are considered. Compared with Cha (1998), the linear regression models are different for seismic intensities (MMI) of VIII to X, which confirms the differences between the worldwide and regional models, and the need to derive a loss-prediction model for any specific area using the appropriate data (Heatwole and Rose 2013). For moderate seismic-prone regions, loss-prediction models for weak seismic intensity (VII) are also relevant, as shown by the moderate earthquake-induced losses referenced in the present dataset (Tables 1, 2).
Economic damage adjusted to 2015 USD value (L $2015) versus GDP.Unit with the regression models for seismic intensities VII–X of the Mediterranean earthquakes examined in this study, compared with the Cha (1998) empirical model results
Table 3 summarizes the results of the regression models for intensities VII–X using Eq. 3. Considering R 2, the model fits are relatively good, at 0.62–0.76, and is as good as for the models provided by Cha (1998). Regression for losses was also performed considering the exposed population as a predictor variable and using the same regression model form as Eq. 3. Table 4 gives the results of the regression models. As expected and reported by most previous studies, POP.Unit is not as relevant as GDP.Unit for the economic loss models. In this case, the fits of the R 2-based models fall around 0.5, which is notably lower than the values obtained by considering GDP.Unit.
4.2 Economic Losses (L $2015) Versus Earthquake Magnitude, GDP, and Affected Population
Heatwole and Rose (2013) used the magnitude of U.S. earthquakes as a hazard-related predictor variable for loss prediction, and considered the population of the affected area and GDP as exposure-related variables. Assuming a non-normal distribution of the variables, they considered a natural-log model using a conventional form, as follows:
where log indicates the natural log; a, b, and c are the regression coefficients; \(\varepsilon\) is the RMSE; X1 is the hazard-related variable—magnitude or intensity; and X2 is the exposure-related variable—GDP.Unit or POP.Unit. The sparse nature of the data and the minimum number of predictor variables means that these variables are not normally distributed and are considered logged variables.
Table 5 summarizes the regression model coefficients following the original presentation by Heatwole and Rose (2013) using POP.Unit and GDP.Unit to predict the L $2015 losses. Only 57 observations with VI < MMI < XI and with L $2015 and GDP.Unit and POP.Unit information available are considered. As Heatwole and Rose (2013) reported, the regression fit coefficient (adjusted R 2) is higher for GDP.Unit (0.653) than for POP.Unit (0.527), because GDP.Unit is a macroeconomic variable that represents the wealth of the affected region, whereas the population is not. Compared with using the regression forms of Cha (1998) (Tables 3, 4), the same results are observed, which confirms the relevance of GDP rather than population for prediction of economic damage. For GDP.Unit, the coefficient of the regression fit (adjusted R 2) is of the same order of magnitude (0.610 versus 0.653) as for the regional U.S. earthquake-based model (Heatwole and Rose 2013), which also confirms the advantage of using regional earthquake loss databases. However, the magnitude characterizes the actual earthquake and does not take into account any seismic wave attenuation with distance, whereas the macroseismic intensity does. It is therefore reasonable to assume that intensity is a more relevant hazard-related predictor than magnitude. Table 6 gives the economic loss predictions with intensity as the hazard-related predictor variable, in the same manner as the formulation by Cha (1998). The fit model parameters (R 2, adjusted R 2) are higher with intensity than with magnitude, with values comparable to those from Eq. 3 considering GDP.Unit (Table 3), and R 2 close to 0.7. This result shows that intensity is a better hazard-related predictor variable for relevant loss assessment.
4.3 Human Losses Considering Building Damage
Extensive studies have been carried out using building damage as a predictor variable for loss assessment (D’Ayala et al. 1997; Bommer et al. 2002; Goretti and Di Pasquale 2002; Kappos et al. 2006; So and Spence 2013; FEMA 2016), on the premise that damage to structures produces direct and indirect economic losses and fatalities. Damage can indeed be considered as a proxy of intensity, as macroseismic surveys completed after earthquakes are mainly derived from the observed damage for the strongest shaking (> VII). The amount of damage also affects the costs related to reconstruction and business interruption because of loss of use of damaged buildings.
In the present study, extensive data allowed the development and testing of regression models, with the loss estimation based on reduced forms, like those proposed by Heatwole and Rose (2013), but considered on a log10 scale. The human loss variables are the number of homeless and injured people, and the fatalities, while considering the affected population (POP.Unit) as an exposure-related variable. The hazard-related predictor variables are seismic intensity and number of damaged buildings classified as D4 + D5, according to EMS98. In our dataset, the quality of the data is relatively heterogeneous, with some references indicating the numbers of casualties with accuracy to the unit, while others indicating rounded quantities, and thus introducing uncertainty into the regression models. The primary objective of the present study was also to develop prediction models for the Mediterranean region, with special focus on Algeria, and here the Algerian earthquakes are defined separately from the total dataset in each analysis.
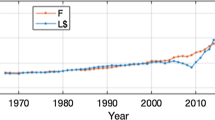
Figure 4 shows as an example the distribution of human losses versus damage (Fig. 4a) and intensity (Fig. 4b) for all of the earthquakes. Exposed population is not considered here.
Table 7 summarizes all of the analysis results related to the regression fits, with RMSE and adjusted R 2. Table 7 and Fig. 4 show that for injuries (I) and fatalities (F), the models show low fits compared to those for home loss (H). Considering the whole dataset of earthquakes and intensities as the predictor variables (Fig. 4b, Table 7), low-fit models were derived, with adjusted R 2 of 0.23, 0.34, and 0.42 for the H, I, and F human loss variables, respectively. These values were significantly improved to become 0.72, 0.49, and 0.44, respectively when the damage was used as the predictor variable (Fig. 4a, Table 7). These models show the lowest RMSE values, which confirm the relevance of damage as a predictor of casualties. Furthermore, a reduced-form model that considered simultaneously intensity and damage was tested (Table 7), and the fits did not improve significantly (0.73, 0.53, and 0.54, respectively). Despite the significant relevance of damage as a hazard-related variable, the fits remained low, which resulted in imprecise assessment when using these models. However, when considering the Algerian earthquakes only (Table 7), the fits are considerably improved, reaching 0.98, 0.72, and 0.57, respectively, although this is based on a small amount of data and is not sufficiently representative statistically. This does suggest that regional data-based models that integrate urban features (regional typology, building design, and quality of construction) can improve loss prediction models that consider building damage, which is not the case for the reduced-form regression model that considers intensity and the Algerian earthquakes only (Table 7; with adjusted R 2 of 0.43, 0.28, and 0.37, respectively).
The relevance of building damage as a predictor variable is also confirmed for economic losses. Table 8 gives the economic losses adjusted to 2015 USD value (L $2015) considering GDP.Unit and damage as the exposure-related and hazard-related variables of the reduced-form model. Compared with the fits given in Table 6, which consider intensity as the hazard-related variable, the adjusted R 2 increases to 0.72 (from 0.70) and the RMSE decreases a little to 0.55 (compared with 0.56).
As human losses depend on the exposed population, as suggested by Samardjieva and Badal (2002) for a worldwide model, here a Mediterranean model was also derived that considered the exposed population (POP.Unit) and damage. Table 7 presents the results of the regression, with significant improvements to the fits given previously in Table 7, whereby R 2 reached 0.77, 0.58, and 0.48, for H, I, and F, respectively. These values were further improved when only the Algerian earthquakes were considered (Table 7), with values of 0.98, 0.75, and 0.67, respectively, which is also the case when damage is used instead of intensity (Table 7).
The relevance of damaged buildings in models of economic and human losses is confirmed by this analysis as well as the evident needs to consider exposed population for human losses. Combining damage as hazard-related variable and GDP or exposed population as exposure-related variables improve the accuracy of the prediction. Nevertheless, damage prediction is more challenging than intensity or magnitude for real-time predictions and especially for regions with no available building inventory or large-scale vulnerability models. New, rapid methods for large-scale damage estimation are becoming more readily available. These practices are based on statistical analysis or data mining of urban data derived from satellite remote sensing (Saito and Spence 2011) or national census databases (Pittore and Wieland 2013; Riedel et al. 2014, 2015; Guettiche et al. 2017).
5 The Constantine (Algeria) Case
In this section, the loss models developed in this study are applied to the city of Constantine, Algeria. We considered the Constantine environment to be suitable for testing the empirical relationships derived in the previous section, without having as an objective a full and extended seismic-risk analysis that includes a site-specific hazard assessment. Constantine is the third largest city in Algeria in terms of population and economic activities. It is located in Algeria’s most seismically active region (acceleration, 0.129 g in the Algerian Seismic Hazard Map), and it has suffered several earthquakes in the past (Benouar 1994), including the strongest felt historical earthquake in 1985 of intensity VIII. Guettiche et al. (2017) performed a seismic vulnerability analysis of this area based on methods developed by Riedel et al. (2014) and Riedel et al. (2015), which were validated by comparing classical in situ engineering survey results. The elementary information provided by remote sensing and the national census (for example, period of construction, number of stories) was used to assess seismic vulnerability. We used the EMS98 damage matrix for intensities VII–X to compute seismic damage (D4 + D5) for each intensity. Our study is not focused primarily on the Constantine loss assessment for a realistic earthquake scenario, but more as a case study to provide insights on the uncertainties of the loss model related to the database. Only the damage-related scenarios given in Guettiche et al. (2017) were considered for testing the loss models for intensities VII–X.
The population of Constantine in 2008 was around 1 million, according to the National Office of Statistics.Footnote 7 The area considered in the present study is highly populated and is characterized by dense neighborhoods composed of old residential buildings. In terms of the urban surface area affected by the scenario earthquake defined by Guettiche et al. (2017), there is an exposed population (POP.Unit) of 100,000 inhabitants. The GDP per capita of Algeria is USD 4152.77Footnote 8 and for the area considered, GDP.Unit can be defined as follows:
The reduced-form models defined in Table 6 for the economic losses and Table 7 for the human losses (home loss, injuries, fatalities) were applied to the area considered for Constantine. Table 9 summarizes the result for the seismic intensities of VII–X. It provides information related to building damage and economic and/or human impact, which are also key elements in performance-based, earthquake-engineering approaches. In Constantine the total number of damaged buildings was between 195 (VII) and 1654 (X), which produced mean loss indicators for home loss, injured persons (injuries), and fatalities of 6067, 157, and 91, respectively, and economic losses of about USD 200 million.
It is worth noting that the uncertainty here is relatively high, which results from the uncertainties related to the information in the database. However, decision makers are not directly concerned with magnitude, building damage, or intensity, but rather pay attention to performance indices for loss and injuries to occupants, or the homeless people that need to be sheltered in the event of a seismic disaster. Compared with previous studies, this integration of building damage as a hazard-related parameter improves the prediction, and should thus be incorporated into the analysis of earthquake losses. Furthermore, data collection after earthquakes should be improved.
6 Conclusions
This study provided a compilation of data and empirical models to estimate the economic and human impacts of earthquakes in the Mediterranean region. Earthquakes are complex and rare events, and post-earthquake information has to be carefully scrutinized before regression models can be developed. But there is the need to define performance metrics that are relevant for decision makers and seismic risk mitigation. Generally speaking, these metrics relate to the risks of casualties for anticipation of the short-term responses to an emergency, such as home loss and personal injuries, and anticipation of economic losses and fatalities for the long-term recovery processes. In this study, data related to 65 earthquakes in the Mediterranean region were compiled in a comprehensive database, with particular attention paid to Algeria. Reduced-form models were then derived, based on hazard-related and exposure-related variables. Because building damage is a key indicator related to losses, we have demonstrated that the integration of such information into regional models improves the loss assessment by reducing the computed regression errors R 2. These parameters require extensive analysis of the area considered in terms of building vulnerability, but new data sources such as remote sensing and national census information, when coupled with data mining algorithms, promise to provide new perspectives for cost-effective and relevant ways to determine seismic damage to buildings.
Vulnerability of buildings is an essential element, since damage seems to be the critical element to define the hazard-related parameters. Riedel et al. (2014, 2015), and Guettiche et al. (2017) have shown that large scale-based methods for vulnerability assessment can provide relevant forecasting of damage (D4 + D5) for a given seismic intensity. These methods are based on information that describes the general characteristics of the regional typology of structures and their particular attributes, such as those that might be obtained by satellite imagery. In this way, loss models can be improved everywhere by integrating the spatial variability of local vulnerability in the concerned regions. Efforts to study additional predictor variables, such as population mobility during the day (exposure-related) and physical characterization of the hazard that use ground-motion parameters, are necessary in further research.
Notes
References
AFPS (Association Française de Génie Parasismique). 2003. Preliminary report of the survey done after the Algerian, 21/05/2003 earthquake (Rapport préliminaire de la mission du séisme du 21 mai 2003 en Algérie). http://www.afps-seisme.org/Publications/Rapports-de-missions/Algerie-2003/. Accessed Jul 2016.
Akoglu, A.M., A.Z. Cakir, M. Meghraoui, S. Belabbes, S.O. El Alami, S. Ergintav, and H.S. Akyüz. 2006. The 1994–2004 Al Hoceima (Morocco) earthquake sequence: Conjugate fault ruptures deduced from InSAR. Earth and Planetary Science Letters 252(3): 467–480.
El Alami, S.O., B. Tadili, L.A. Brahim, and I. Mouayn. 2004. Seismicity of Morocco for the period 1987–1994. Pure and Applied Geophysics 161(5–6): 969–982.
Altinok, Y., B. Alpar, N. Özer, and C. Gazioglu. 2005. 1881 and 1949 earthquakes at the Chios-Cesme Strait (Aegean Sea) and their relation to tsunamis. Natural Hazards Earth System Science 5(5): 717–725.
Armenian, H.K., A. Melkonian, E.K. Noji, and A.P. Hovanesian. 1997. Deaths and injuries due to the earthquake in Armenia: A cohort approach. International Journal of Epidemiology 26(4): 806–813.
Ayadi, A., and M. Bezzeghoud. 2015. Seismicity of Algeria from 1365 to 2013: Maximum observed intensity map (MOI2014). Seismological Research Letters 86(1): 1–9.
Ayadi, A., F. Ousadou-Ayadi, S. Bourouis, and H. Benhallou. 2002. Seismotectonics and seismic quietness of the Oranie region (western Algeria): The Mascara earthquake of August 18th 1994, Mw = 5.7, Ms = 6.0. Journal of Seismology 6(1): 13–23.
Aydan, O., R. Ulusay, H. Kumsar, and E. Tuncay, 2000. Site investigation and engineering evaluation of the Duzce-Bolu earthquake of November 12, 1999. Technical report, Turkish Earthquake Foundation, TDV/DR 09–51. http://www.turkiyedepremvakfi.org.tr/pdf/deprem_raporlari_sirali/TDV-DR_09-51.pdf. Accessed Jul 2016.
Aysan, F.Y. 1984. The Erzurum-Kars earthquake of Eastern Turkey (1983). Disasters 8(1): 21–32.
Azzouz, H., and B. Rebzani. 2005. Practices of post-seismic evaluation of buildings from El Asnam 1954 to Boumerdes 2003 earthquakes (Evaluation des interventions post-sismiques sur les constructions, D’El-Asnam 1954 à Boumerdès 2003). Report CTC Chlef, Algerie (in French).
Azzouz, H. 2002. History of the 10/10/1980 Chlef (El Asnam) earthquake (Historique du séisme de Chlef, ex-El Asnam du 10/10/1980). In 3ème forum des assurances sur les CAT-NAT, El-Aurassi, 13–15 October 2002, 120–137 (in French).
Badal, J., M. Vázquez-Prada, and A. González. 2005. Preliminary quantitative assessment of earthquake casualties and damages. Natural Hazards 34(3): 353–374.
Baratta, M. 1910. The Calabrian seismic catastrophe of Messina (December 28, 1908) (La catastrofe sismica calabro messinese (28 dicembre 1908)). Relazione alla Società Geografica Italiana, 2 vol., Roma (riproduzione integrale nel DVD-Rom allegato a Il terremoto e il maremoto del 28 dicembre 1908). INGV resources. https://ingvterremoti.wordpress.com/2015/12/28/i-terremoti-del-900-la-catastrofe-sismica-del-28-dicembre-1908/. Accessed Jul 2016.
Barbano, M.S., R. Azzaro, and D.E. Grasso. 2005. Earthquake damage scenarios and seismic hazard of Messina, north-eastern Sicily (Italy) as inferred from historical data. Journal of Earthquake Engineering 9(6): 805–830
Barka, A. 1999. The 17 August 1999 Izmit earthquake. Science 285(5435): 1858–1859
Benouar, D. 1994. Material for the investigation of the seismicity of Algeria and adjacent region during the twentieth century. Annals of Geophysics 37(4): 860.
Benson, C., and J. Twigg. 2004. Measuring mitigation: Methodologies for assessing natural hazard risks and the net benefits of mitigation—A scoping study. International Federation of Red Cross and Red Crescent Societies/the ProVention Consortium. http://www.preventionweb.net/publications/view/1065. Accessed Jul 2016.
Bertero, V., and H. Shah. 1983. El-Asnam, Algeria, earthquake of October 10, 1980: A reconnaissance and engineering report. https://www.eeri.org/lfe/pdf/algeria_el_asnam_eeri_preliminary_report_1.pdf. Accessed Jul 2016.
Berz, G., and E. Hettler. 1981. Earthquakes in Greece, Februray/March 1981. EERI report. https://www.eeri.org/lfe/pdf/Greece_AlcionidesIsles_Berz&Hettler_Nov81.pdf. Accessed Jul 2016.
Bird, J.F., and J.J. Bommer. 2004. Earthquake losses due to ground failure. Engineering Geology 75(2): 147–179.
Bommer, J., R. Spence, M. Erdik, S. Tabuchi, N. Aydinoglu, E. Booth, D. del Re, and O. Peterken. 2002. Development of an earthquake loss model for Turkish catastrophe insurance. Journal of Seismology 6(3): 431–446.
Brookshire, D., S. Chang, H. Cochrane, R. Olson, A. Rose, and J. Steenson. 1997. Direct and indirect economic losses from earthquake damage. Earthquake Spectra 13(4): 683–701.
CATDAT (Damaging earthquake database). 2016. Earthquake-Report.com. http://earthquake-report.com/. Accessed Jul 2016.
CGS (National Center for Applied Research in Earthquake Engineering). 2000. The 1999/12/22 Ain-Temouchent earthquake (Séisme de Ain-Temouchent du 22 décembre 1999). Report n°2, Centre National de Recherche Appliquée en Génie Parasismique (CGS), Algier (Algeria) (in French).
Cha, L.S. 1998. Assessment of global seismic loss based on macroeconomic indicators. Natural Hazards 17(3): 269–283.
Chen, Q.F., Y. Chen, and L. Chen. 1997. Earthquake loss estimation with GDP and population data. Acta Seimologica Sinica 10(4): 791–800.
Chen, Y., Q.F. Chen, and L. Chen. 2001. Vulnerability analysis in earthquake loss estimate. Natural Hazards 23(2–3): 349–364.
Cherkaoui, T., and M. Harnafi. 2004. Field survey from the 3rd to 7th March 2004 (Rapport préliminaire de mission du 3 au 7 mars 2004). Université Mohammed V—Agdal, Département de Physique du Globe. http://ashabarter.free.fr/Basedocuments/SeismeAlHoceima.pdf. Accessed 28 Nov 2017.
Clerc, D. 1975. Economics of Algeria (Economie de l’Algérie). Ministère de l’intérieur, France (in French).
Coburn, A., and R. Spence. 2002. Earthquake protection, 2nd edn. Chichester: John Wiley & Sons.
Daniell, J.E., B. Khazai, F. Wenzel, and A. Venvaeck. 2011. The CATDAT damaging earthquakes database. Natural Hazards and Earth System Science 11(8): 2235–2251.
Daniell, J.E., A. Vervaeck, and F. Wenzel. 2010. The cost of historic earthquakes today—Economic analysis since 1900 through the use of CATDAT. In Proceedings of Australian Earthquake Engineering Society 2010 Conference, 26–28 November 2010, Perth, Western Australia.
Dunbar, P., R. Bilham, and M. Laituri. 2002. Earthquake loss estimation for India based on macroeconomic indicators. In Risk science and sustainability: Science for reduction of risk and sustainable development of society, ed. T. Beer, and A. Ismail-Zadeh, 163–180. Dordrecht: Kluwer Academic Publishers.
D’Ayala, D., R. Spence, C.S. Oliveira, and A. Pomonis. 1997. Earthquake loss estimation for Europe’s historic town centres. Earthquake Spectra 13(4): 773–793.
EERI (Earthquake Engineering Research Institute). 2012. The Mw 7.1 Erciş-Van, Turkey earthquake of October 23, 2011. EERI Special earthquake report. https://www.eeri.org/wp-content/uploads/Van_Turkey_eq-report.pdf. Accessed Jul 2016.
EERI (Earthquake Engineering Research Institute). 1986. The September 13, 1986 earthquake—Kalamata, Greece. EERI special earthquake report. https://www.eeri.org/lfe/pdf/Greece_Kalamata_Insert_Oct86.pdf. Accessed Jul 2016.
EERI (Earthquake Engineering Research Institute). 1992. The Cairo, Egypt, earthquake of October 12, 1992. EERI special report. https://www.eeri.org/lfe/pdf/Egypt_Cairo_Insert_Dec92.pdf. Accessed Jul 2016.
EERI (Earthquake Engineering Research Institute). 1995. The Egion, Greece, earthquake of June 15, 1995. EERI special report. https://www.eeri.org/lfe/pdf/Greece_Egion_Insert_Jul95.pdf. Accessed Jul 2016.
EERI (Earthquake Engineering Research Institute). 1998. Turkish earthquakes: Two reports; lessons from Adana—Ceyhan quake and Dinar aftershock. EERI special earthquake report. https://www.eeri.org/lfe/pdf/Turkey_Adana_Ceyhan_Insert_Sep98.pdf. Accessed Jul 2016.
EERI (Earthquake Engineering Research Institute). 1999. The Athens, Greece, earthquake of September 7, 1999. EERI newsletter. https://www.eeri.org/lfe/pdf/Greece_Athens_Article_Oct99.pdf. Accessed Jul 2016.
EERI (Earthquake Engineering Research Institute). 2003. Preliminary observations on the October 31–November 1, 2002 Molise, Italy, earthquake sequence. EERI special earthquake report. https://www.eeri.org/lfe/pdf/italy_molise_eeri_report.pdf. Accessed Jul 2016.
EERI (Earthquake Engineering Research Institute). 2004. Preliminary observations on the Al Hoceima, Morocco, Earthquake of February 24, 2004. https://www.eeri.org/lfe/pdf/morocco_alhoceimaeeripreliminary_report.pdf. Accessed Jul 2016.
Erdik, M. 1984. Report on the Turkish earthquake of October 30, 1983. Earthquake Spectra 1(1): 151–172.
Erdik, M., K. Sesetyan, M.B. Demircioglu, U. Hancilar, and C. Zulfikar. 2011. Rapid earthquake loss assessment after damaging earthquakes. Soil Dynamics and Earthquake Engineering 31(2): 247–266.
FEMA (Federal Emergency Management Agency). 2016. Hazus-MH MR5 earthquake loss estimation methodology. Technical and user’s manual. Washington, DC: Federal Emergency Management Agency. http://www.fema.gov/plan/prevent/hazus. Accessed Jul 2016.
Ferrer, M., L.G. de Vallejo, J.C. García, A. Rodríguez, and H. Estévez. 2004. Seismic and flood risk evaluation in Spain from historical data. In Engineering geology for infrastructure planning in Europe: A European perspective, ed. R. Hack, R. Azzam, and R. Charlier, 727–737. Berlin: Springer.
Goretti, A., and G. Di Pasquale. 2002. An overview of post-earthquake damage assessment in Italy. EERI workshop on an action plan to develop earthquake damage and loss data protocols, 19–20 September 2002, Pasadena, California. https://www.eeri.org/lfe/pdf/italy_molise_goretti_pasadena_paper.pdf. Accessed Jul 2016.
Guettiche, A., P. Guéguen, and M. Mimoune. 2017. Seismic vulnerability assessment of a typical Algerian urbanization using association rule learning—Application to the city of Constantine, Algeria. Natural Hazards 86(3): 1223–1245.
Guha-Sapir, D., R. Below, and P. Hoyois. 2016. EM-DAT: International disaster database. Université Catholique de Louvain, Belgium. http://www.emdat.be. Accessed Mar 2016.
Guéguen, P., H. Yepes, and I. Riedel. 2016. On the value of earthquake scenario: The Kathmandu recent lesson. Frontiers in Built Environment. https://doi.org/10.3389/fbuil.2015.00026.
Guéguen, P. 2013. Seismic vulnerability of structures. Civil Engineering and geomechanics series. Hoboken, US: Wiley–ISTE (International Society for Technology in Education).
Hatzfeld, D., V. Karakostas, M. Ziazia, G. Selvaggi, S. Leborgne, C. Berge, R. Guiguet, A. Paul, P. Voidomatis, D. Diagnourtas, I. Kassaras, et al. 1997. The Kozani-Grevena (Greece) earthquake of 13 May 1995 revisited from a detailed seismological study. Bulletin of the Seismological Society of America 87(2): 463–473.
Heatwole, N., and A. Rose. 2013. A reduced-form rapid economic consequence estimating model: Application to property damage from US earthquakes. International Journal of Disaster Risk Science 4(1): 20–32.
Holzer, T.L., and J.C. Savage. 2013. Global earthquake fatalities and population. Earthquake Spectra 29(1): 155–175.
JAEE (Japan Association of Earthquake Engineering). 2004. Boumerdes earthquake, May 21, 2003. Japanese Reconnaissance Team, Japan Association of Earthquake Engineering report, 151 pp. http://www.jsce.or.jp/library/eq_repo/Vol2/04/algeriareport.pdf. Accessed Jul 2016.
Jackson, J. 2006. Fatal attraction: Living with earthquakes, the growth of villages into megacities, and earthquake vulnerability in the modern world. Philosophical Transactions of the Royal Society A 364(1845): 1911–1925.
Jaiswal, K.S., and D.J. Wald. 2010. An empirical model for global earthquake fatality estimation. Earthquake Spectra 26(4): 1017–1037.
Jaiswal, K.S., and D.J. Wald. 2013. Estimating economic losses from earthquakes using an empirical approach. Earthquake Spectra 29(1): 309–324.
Jaiswal, K.S., D.J. Wald, P.S. Earle, K.A. Porter, and M. Hearne. 2011. Earthquake casualty models within the USGS Prompt Assessment of Global Earthquakes for Response (PAGER) system. In Human casualties in earthquakes, Series Advances in Natural and Technological Hazards Research, ed. R. Spence, E. So, and C. Scawthorn, 83–94. Dordrecht: Springer.
KOERI (Kandilli Observatory and Earthquake Research Institute). 2014. Earthquake report, 24 May 2014 northern Aegean Sea. KOERI report. http://www.koeri.boun.edu.tr/sismo/2/wp-content/uploads/2014/05/KOERI_Press_Bulletin_NAn_EQ_24May2014_v7.pdf. Accessed Jul 2016.
Kappos, A.J., G. Panagopoulos, C. Panagiotopoulos, and G. Penelis, 2006. A hybrid method for the vulnerability assessment of R/C and URM buildings. Bulletin of Earthquake Engineering 4(4): 391–413.
Laouami, N., A. Slimani, Y. Bouhadad, J.-L. Chatelain, and A. Nour. 2006. Evidence for fault-related directionality and localized site effects from strong-motion recordings of the 2003 Boumerdes (Algeria) earthquake: Consequences on damage distribution and the Algerian seismic code. Soil Dynamics and Earthquake Engineering 26(11): 991–1003.
Maddison, A. 2006. The world economy: A millennial perspective. Paris: Organisation for Economic Co-operation and Development (OECD).
Maouche, S., A. Harbi, and M. Meghraoui. 2008. Attenuation of intensity for the Zemmouri earthquake of 21 May 2003 (Mw 6.8): Insights for the seismic hazard and historical earthquake sources in northern Algeria. In Historical seismology: Interdisciplinary studies of past and recent earthquakes, ed. J. Fréchet, M. Meghraoui, and M. Stucchi, 327–350. Dordrecht: Springer.
Martínez-Díaz, J.J., M. Bejar-Pizarro, J.A. Álvarez-Gómez, F. de Lis Mancilla, D. Stich, G. Herrera, and J. Morales. 2012. Tectonic and seismic implications of an intersegment rupture: The damaging May 11th 2011 Mw 5.2 Lorca, Spain earthquake. Tectonophysics 546: 28–37.
Minami, K. 1965. Relocation and reconstruction of the town of Brace, Cyrenaica, Libya damaged by the earthquake of 21 February 1963. UNESCO report, WS/0865.76-AVS, Paris. http://unesdoc.unesco.org/images/0000/000077/007706EB.pdf. Accessed Jul 2016.
Mitchell, A.W. 1976. Reconstruction after disaster: The Gediz earthquake of 1970. Geographical Review 66(3): 296–313.
Molina, S., D.H. Lang, C.D. Lindholm, and F. Lingvall. 2010. User manual for the earthquake loss estimation tool: SELENA. http://selena.sourceforge.net/selenamanual.pdf. Accessed Jul 2016.
NGDC (National Geophysical Data Center). 2016. Significant earthquake database. National Oceanic and Atmospheric Administration (NOAA). http://www.ngdc.noaa.gov/nndc/struts/form?t=101650&s=1&d=1. Accessed Jul 2016.
NYT (New York Times). 1990. 18 dead in quake in Eastern Sicily. New York Times, December 14. http://www.nytimes.com/1990/12/14/world/18-dead-in-quake-in-eastern-sicily.html. Accessed Jul 2016.
Nichols, J.M., and J.E. Beavers. 2003. Development and calibration of an earthquake fatality function. Earthquake Spectra 19(3): 605–633.
Payany, M. 1983. The earthquake of 1909 according to the documents of the time (Le Séisme de 1909 d’après les documents de l’époque). Document technique A: Simulation du séisme provençal de 1909, Centre d’Etudes Techniques de l’Equipement d’Aix-en-Provence. http://observatoire-regional-risques-paca.fr/sites/default/files/biblio/SEI_EVT_1909_SEISME_DOSSIER_TECH_A.pdf. Accessed Jul 2016 (in French).
Pittore, M., and M. Wieland. 2013. Toward a rapid probabilistic seismic vulnerability assessment using satellite and ground-based remote sensing. Natural Hazards 68(1): 115–145.
Protezione Civile. 2002. Molise earthquake 2002, Italy. http://www.protezionecivile.gov.it/jcms/en/terremoto_molise_2002.wp. Accessed Jul 2016.
Psycharis, I. 1978. The Salonica (Thessaloniki) earthquake of June 20, 1978. Caltech report EERL78-03. http://authors.library.caltech.edu/26430/1/7803.pdf. Accessed Jul 2016.
RMS (Risk Management Solutions). 2008. The 1908 Messina earthquake: 100-year retrospective. Special report. http://forms2.rms.com/rs/729-DJX-565/images/eq_1908_messina_eq.pdf. Accessed Jul 2016.
Riedel, I., P. Guéguen, M. Dalla Mura, E. Pathier, T. Leduc, and J. Chanussot. 2015. Seismic vulnerability assessment of urban environments in moderate-to-low seismic hazard regions using association rule learning and support vector machine methods. Natural Hazards 76(2): 1111–1141.
Riedel, I., P. Guéguen, F. Dunand, and S. Cottaz. 2014. Macro-scale vulnerability assessment of cities using association rule learning. Seismological Research Letters 85(2): 295–305.
Rothe, J.P. 1969. The seismicity of the Earth, 1953–1965. Paris: United Nations Educational, Scientific and Cultural Organization (UNESCO). http://unesdoc.unesco.org/images/0001/000145/014503mo.pdf. Accessed Jul 2016.
Saito, K., and R. Spence. 2011. Mapping urban building stocks for vulnerability assessment—Preliminary results. International Journal of Digital Earth 4(Supplemental Issue 1): 117–130.
Samardjieva, E., and J. Badal. 2002. Estimation of the expected number of casualties caused by strong earthquakes. Bulletin of the Seismological Society of America 92(6): 2310–2322.
Samardjieva, E., and K. Oike. 1992. Modelling the number of casualties from earthquakes. Journal of Natural Disaster Science 14(1): 17–28.
Schumacher, I., and E. Strobl. 2011. Economic development and losses due to natural disasters: The role of hazard exposure. Ecological Economics 72: 97–105.
So, E., and R. Spence. 2013. Estimating shaking-induced casualties and building damage for global earthquake events: A proposed modelling approach. Bulletin of Earthquake Engineering 11(1): 347–363.
Storchak, D.A., D. Di Giacomo, I. Bondár, E.R. Engdahl, J. Harris, W.H.K. Lee, A. Villaseñor, and P. Bormann. 2013. Public release of the ISC-GEM global instrumental earthquake catalogue (1900–2009). Seismological Research Letters 84(5): 810–815.
Strauss, J. 1974. If you were the judge. Reading Eagle, April 1974. https://news.google.com/newspapers?nid=1955&dat=19740414&id=LAQrAAAAIBAJ&sjid=x5cFAAAAIBAJ&pg=6853,1396218&hl=en. Accessed Jul 2016.
Turkish Red Crescent Society. 2006. 1999-Marmara earthquake case study. International disaster response law report. http://www.ifrc.org/PageFiles/93724/report-turkey.pdf. Accessed Jul 2016.
US Geological Survey. 2016. Prompt assessment of global earthquakes for response. PAGER system. http://earthquake.usgs.gov/data/pager/. Accessed Jul 2016.
Valcárcel, J.A., G.A. Bernal, and M.G. Mora. 2012. Lorca earthquake May 11 2011: A comparison between disaster figures and risk assessment outcomes. In Proceedings of the 15th World Conference on Earthquake Engineering, 24–28 September, Lisboa, Portugal, 14075.http://www.iitk.ac.in/nicee/wcee/article/WCEE2012_2371.pdf. Accessed 1 Dec 2017.
WHO (World Health Organization). 2016. Global health observatory data: Urban population growth. http://www.who.int/gho/urban_health/situation_trends/urban_population_growth_text/. Accessed Nov 2017.
Whitehead, J., and A. Rose. 2009. Estimating environmental benefits of natural hazard mitigation with data transfer: Results from a benefit-cost analysis of Federal Emergency Management Agency hazard mitigation grants. Mitigation Adaptive Strategy for Global Change 14(7): 655–676.
World Bank. 1994. Memorandum and recommendation of the president of the IBRD to the executive directors on a proposed loan in the amount equivalent to US$51.0 million to the Democratic and popular Republic of Algeria for an emergency reconstruction project. World Bank report No. P-6455-AL, Washington, DC. http://documents.worldbank.org/curated/en/217981468192267567/Algeria-Emergency-Reconstruction-Project. Accessed Jul 2016.
World Bank. 2000. Algeria—Ain Temouchent Emergency Earthquake Recovery Project. World Bank report No. 20297-AL, Washington DC. http://documents.worldbank.org/curated/en/961911468742560729/Algeria-Ain-Temouchent-Emergency-Earthquake-Recovery-Project. Accessed Jul 2016.
Yanev, P.I. 1975. The Lice, Turkey, earthquake of September 6 (reconnaissance report), Technical communication. EERI newsletter 9:6B, URS/Blume San Francisco, California. https://caltech.tind.io/record/597790. Accessed Jul 2016.
Yelles-Chaouche, A., H. Djellit, H. Beldjoudi, M. Bezzeghoud, and E. Buforn. 2004. The Ain Temouchent (Algeria) earthquake of December 22nd, 1999. Pure and Applied Geophysics 161(3): 607–621.
Acknowledgements
The MAIF Foundation supported this work. Institute nationale de la statistique et des études économique (INSEE—National Institute of Statistics and Economic Studies) data were prepared and provided by the Centre Maurice Halbwachs (CMH). This study was sponsored by the Urban Seismology project at the Institute of Earth Science ISTerre of the University of Grenoble-Alpes and by a grant from the Observatoire des Sciences de Univers de Grenoble (The Grenoble Observatory for Sciences of the Universe—Labex OSUG@2020) (Investissements d’avenir, ANR10-LABX56). We thank the two anonymous reviewers for their constructive remarks and comments and the editors of the journal for the editing work.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Guettiche, A., Guéguen, P. & Mimoune, M. Economic and Human Loss Empirical Models for Earthquakes in the Mediterranean Region, with Particular Focus on Algeria. Int J Disaster Risk Sci 8, 415–434 (2017). https://doi.org/10.1007/s13753-017-0153-6
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13753-017-0153-6