Abstract
Based on model structures with atomic resolution, a coarse-grained model for the nucleosome geometry was implemented. The dependence of the chromatin fiber conformation on the spatial orientation of nucleosomes and the path and length of the linker DNA was systematically explored by Monte Carlo simulations. Two fiber types were analyzed in detail that represent nucleosome chains without and with linker histones, respectively: two-start helices with crossed-linker DNA (CL conformation) and interdigitated one-start helices (ID conformation) with different nucleosome tilt angles. The CL conformation was derived from a tetranucleosome crystal structure that was extended into a fiber. At thermal equilibrium, the fiber shape persisted but relaxed into a structure with a somewhat lower linear mass density of 3.1 ± 0.1 nucleosomes/11 nm fiber. Stable ID fibers required local nucleosome tilt angles between 40° and 60°. For these configurations, much higher mass densities of up to 7.9 ± 0.2 nucleosomes/11 nm fiber were obtained. A model is proposed, in which the transition between a CL and ID fiber is mediated by relatively small changes of the local nucleosome geometry. These were found to be in very good agreement with changes induced by linker histone H1 binding as predicted from the high resolution model structures.
INTRODUCTION
In eukaryotes, the DNA inside the nucleus is organized by histone proteins into a nucleoprotein complex referred to as chromatin (1). The dynamic organization of chromatin has been identified as a major regulatory factor for molecular biological processes such as replication, transcription, repair, and recombination, as it controls the accessibility of chromatin for DNA binding factors (2–4). Accordingly, the principles that govern chromatin structure are an important subject of current research. The main building block of chromatin is the nucleosome. It consists of an octameric complex of core histones H2A, H2B, H3, and H4, around which ∼147 basepairs (bp) of DNA are wrapped in 1.67 turns in a left-handed superhelix. This complex is called the nucleosome core particle. Several structures of the free histone octamer and of the nucleosome core complex have been determined by high resolution x-ray diffraction as reviewed recently (5). Nucleosomes show a regular spacing on the DNA chain and are separated by a “linker” DNA that varies in length for different organisms (1). The total nucleosomal repeat length (NRL) covers the range of 165–220 bp with NRLs of ∼188 bp and ∼196 bp being the most abundant (6). A fifth histone, the so-called linker histone, organizes the linker DNA (7–9). The binding of linker histones protects an additional ∼22 bp of DNA flanking the nucleosome structure, and constrains the DNA entry/exit angle such that a more compact chromatin conformation is adopted (7,8,10–15). The complex of the nucleosome core plus linker histone and the associated ∼169 bp of DNA is referred to as the chromatosome. The structure of the chromatosome is unknown, and various models have been proposed for the integration of linker histone H1 or its globular domain into the nucleosome (7,16–19).
At physiological salt concentration, longer nucleosome chains can reversibly fold into a fiber characterized by a diameter of ∼30 nm (1,3,20,21). Intriguingly, the distribution of linker lengths is not random but follows a ∼10 bp periodicity, which closely resembles one helical turn of DNA (6). Various models for the fiber geometry are currently under investigation. They can be classified into two groups: those with a continuous solenoidal wrapping of the nucleosome chain (one-start helix) or a zig-zag organization of nucleosomes where the DNA crosses the fiber center (two-start helix). Other characteristic features of the fiber conformation are the orientation of nucleosomes to the helix axis (nucleosome tilt angle), the position of the linker histones, the degree of linker DNA bending, and the ability to accommodate different NRLs (1,21). Following the experimental analysis of chromatin, two different types of two-start helix conformations with crossed-linker DNA are distinguished here. The first one was proposed for native chromatin fibers extracted from chicken erythrocytes that show a zig-zag like DNA backbone with a so-called nucleosome stem motif (10). In this nucleosome stem, the linker histone H5 mediates the association of the two DNA segments, leaving the nucleosome core particle over a distance of 3–5 nm before the linker DNA diverges. This type of fiber was not considered in this work, but results on its analysis are reported in the companion article (22). The second model of a two-start fiber helix is based on the crystal structure of a tetranucleosome particle (23). This structure has a short NRL of 169 bp and was determined in the absence of linker histones. The tetranucleosome unit can be extended into a fiber model with a predicted mass density of 5.5 nucleosomes/11 nm fiber length. The resulting conformation with crossed-linker (CL) DNA backbone is referred to here as CL fiber. Finally, a third structure belonging to the one-start helix class was derived recently from electron microscopy studies of chromatin fibers with longer repeat lengths (177–237 bp) and one linker histone per nucleosome (24). Its characteristic features are the interdigitation of nucleosomes (ID conformation) that results in a high compaction value of 11–15 nucleosomes/11 nm fiber. It is related to a model structure for an ID fiber proposed by Daban (25), but the two ID fibers are distinct with respect to the nucleosome tilt angle. As suggested by Robinson and Rhodes, the apparent differences between the CL and the ID fiber conformations can be reconciled, if the CL fiber is regarded as the structure of the nucleosome chain in the absence of linker histone while its presence can induce a transition to the more compacted ID fiber (21). It is noted that the experimental results on the structure of the CL and the ID fiber organization were obtained with nucleosome chains reconstituted on DNA fragments with equally spaced high affinity nucleosome positioning sequences. Accordingly, they are likely to represent structures that are more regular than those obtained with natural DNA sequences, for which small variations in nucleosome spacing are expected.
Here, we derived high resolution models for the chromatosome complex based on the nucleosome conformation found in the tetranucleosome particle (23) and previous chromatosome models (17–19). A coarse-grained model was developed from these structures to describe the local geometry of the nucleosome/chromatosome. The equilibrium conformation of the corresponding chains composed of 100 nucleosomes was investigated by Monte Carlo (MC) simulations. This type of analysis has been applied successfully in previous studies to explore the conformation of nucleosomal arrays and chromatin fibers (26–30). In the work presented here, this approach is extended by more detailed description of the nucleosome geometry and a newly developed nucleosome-nucleosome interaction potential. The latter is described in detail in the companion article in conjunction with improved sampling methods (22). The results identify structural requirements for the formation of chromatin fibers, and relate the local nucleosome geometry to the formation of distinct higher order chromatin states.
MATERIALS AND METHODS
Nucleosome and chromatosome structures
Several structures with resolutions in the range of 2–4 Å of the nucleosome core particle have been reported (5), yet the exact details of the chromatosome are still under investigation. Since the path of the linker DNA between nucleosomes was expected to be an important parameter of our modeling work, a nucleosome structure with associated linker DNA was extracted from the Protein Data Bank coordinates of the tetranucleosome particle (23) (Fig. 1 A). In addition, three different chromatosome models were derived from previously proposed high resolution structures (17–19). A detailed characterization of these models will be reported elsewhere. Briefly, the following approach was used: The complex of linker histone H1 with two bound DNA strands was taken from the chromatosome model proposed by Bharath et al. (18). This complex was incorporated into the nucleosome structure with a slightly altered positioning of H1 to obtain the structure shown in Fig. 1 B. The two other published model structures of the chromatosome consisted of the nucleosome with the globular domain of the linker histone H5 (17,19). This sequence was replaced with that of H1 with the added C-terminal domain (Fig. 1, C and D).
FIGURE 1.
Nucleosome and chromatosome model structures with different entry-exit geometries of the DNA. (A) Nucleosome with 199 bp of DNA from the tetranucleosome crystal structure (23). The interactions among the nucleosomes lead to some bending of the linker DNA. (B) Chromatosome model with 213 bp of DNA derived from Bharath et al. (18). (C) Chromatosome model with 215 bp of DNA derived from Brown et al. (17). (D) Chromatosome model with 215 bp of DNA derived from Fan et al. (19).
All structures were subjected to energy minimizations with the Amber 9 software package (31) using the Cornell et al. force field (32). Steric clashes were cleaned up by energy minimization and short molecular dynamics simulations (100 ps) with a generalized Born solvent-accessible surface model (ionic strength 150 mM, ɛinternal = 1.0, ɛexternal = 78.5) (33,34). The particle mesh Ewald method (35) for nonperiodic-calculations was used for the treatment of electrostatic interactions. The root mean-square of the Cartesian elements of the gradient was required to be <0.05 kcal mol−1 Å−1 as convergence criterion for the energy gradient. Construction and visualization of the models were done with Visual Molecular Dynamics 1.8.6 (36) and Sybyl 7.1 software (Tripos, St. Louis, MO).
Monte Carlo simulations
Representative equilibrium ensembles of chromatin fiber configurations, referred to as a trajectory, were calculated using MC simulations with a coarse-grained chromatin fiber model. In this model, nucleosomes were approximated by cylinders and connected by two linker DNA segments. The parameters describing harmonic bend, torsion, and stretch potentials of the linker DNA and a Debye-Hückel approximation for electrostatics were those introduced by Wedemann and Langowski (27), and are listed in the Supplementary Material (Table S1).
The interactions between nucleosomes were described by an oblate spherocylinder potential (22,37), which represents the shape of the nucleosome core particle more accurately than the previously used ellipsoidal potential (22). The parameters of the potential are shown in the Supplementary Material, Table S1 of Data S1. A Metropolis MC algorithm and a replica exchange procedure were applied to sample the configuration space via rotation and pivot moves of the linker DNA and the nucleosomes (22,27). The influence of the initial configuration was assessed by starting the simulations for all fiber conformations listed in Tables 1, 2, and 3 either from fiber structures with relaxed DNA bend, stretch, and torsion potentials or from a stretched, straight nucleosome chain (Supplementary Material, Fig. S1, Data S1). Furthermore, a replica exchange algorithm preceded by an initial annealing step was applied for selected nucleosome geometries from the three different fiber types (22). This algorithm reduced the trapping of configurations in local energy minima, and was found to be advantageous for nucleosome geometries that converged only slowly toward thermal equilibrium. Typically, after ∼107 MC steps (depending on the local geometry), thermal equilibrium was reached, as judged from arriving at a steady state of the total energy, the fiber shape coefficient, fiber mass density, and the average end-to-end distance of the chain. For the two start configurations (relaxed or stretched out), the final ensembles yielded the same results with respect to the total energy, fiber shape, mass density, fiber diameter, and persistence length within the limits of the standard deviation.
Evaluation of trajectories
Once the thermal equilibrium was reached, the different nucleosome geometries were simulated for an additional 8 × 107 MC steps at a temperature of 293 K. This part of the trajectory was then used to evaluate the fiber properties. Based on an autocorrelation analysis of the configurations with respect to the energy, the mass density, the fiber shape, and other parameters, ∼400 statistically independent equilibrium conformations were selected. The trajectories were analyzed in terms of the global shape of the nucleosome chain, its linear mass density, fiber diameter, and persistence length. Mass density and fiber diameter were computed as described previously (27). To evaluate the fiber shape, three different approaches were used:
A fiber shape coefficient (FSC) was determined as described in the companion article (22). Briefly, the geometrical center for a part of the chain that contained ∼13 nucleosomes connected by their linker DNA was computed. At this point, the radius of a sphere was chosen such that it contained the 13 nucleosomes and their linker DNA, representing N elements. Then the number Nsphere of all nucleosomes and linker DNA segments in this sphere was determined. The ratio N/Nsphere defines the FSC of the configuration. FSC values of ∼0.5 or below represented a globular organization of the chain as the number of nucleosomes and linker DNA segments from other parts of the chain reached the value of N. In contrast, a value of 1.0 corresponds to a fiber shaped structure that contains no “foreign” nucleosomes or linker DNA.
A principal components analysis (PCA) was conducted to determine the shape of the simulated structures. A scalene ellipsoid was fitted to the configurations where the ellipsoid half axes were determined from the eigenvalues of the covariant matrix of the nucleosome positions. The mean ratio of the longest and shortest half axis was used to categorize the overall fiber shape. A spherical volume has a PCA ratio of 1, whereas a PCA ratio >3 was required here to classify a trajectory as fiber-shaped.
- Sedimentation s and diffusion coefficients D at 20°C in water were calculated from the fiber trajectories using the program Hydro (38). Nucleosomes were represented as spheres of 5.5 nm radius whereas the linker DNA was modeled as a string of beads with a radius of 1.2 nm. The mass M of a fiber was calculated using a molecular mass of 108.5 kDa for the histone core, 24 kDa for histone H1, if present, and 0.66 kDa per basepair of DNA. The partial specific volume,
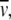 was determined from values of 0.746 cm3 g−1 for the histones and 0.55 cm3 g−1 for the DNA. The value of s includes the contribution from both the mass and the shape of the particle as given by its friction coefficient f, whereas D only reflects the shape according to Eq. 1:
was determined from values of 0.746 cm3 g−1 for the histones and 0.55 cm3 g−1 for the DNA. The value of s includes the contribution from both the mass and the shape of the particle as given by its friction coefficient f, whereas D only reflects the shape according to Eq. 1: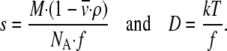
(1)
In Eq. 1, ρ is the density of the solvent and NA Avogadro's number. The expressions can be combined into the Svedberg equation to relate s, D, and M:
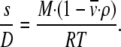 |
(2) |
The persistence length P was calculated according to Eq. 3 from the mean-squared end-to-end distance using the Kratky-Porod model (see Rippe (39) and references therein):
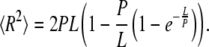 |
(3) |
In a flexible, but inextensible, worm-like chain, the end-to-end distance R depends on the contour length L and the persistence length. The contour length and the end-to-end distance of the MC simulated fibers were calculated from the fiber backbone as defined by the geometrical centers of the spheres used in the FSC calculations.
RESULTS
A coarse-grained model based on high resolution structures of nucleosomes
Four different structural models of nucleosomes derived from x-ray structures and molecular modeling were selected to develop coarse-grained models of the local nucleosome geometry. These were then implemented for MC simulations of nucleosome chains with 100 nucleosomes to investigate how the folding of the chain depends on the local nucleosome geometry. For nucleosomes including the associated linker DNA but without linker histone, the tetranucleosome crystal structure (23) was used as a reference (Fig. 1 A). The different nucleosome conformations with bound linker histone H1 (chromatosome) were derived from previous structures based on homology modeling (18), mutagenesis experiments (17), and computer docking simulations (19). In the latter two models, the globular domain of the linker histone was extended to the complete linker histone H1 using the model of Bharath et al. (18). These structures were then optimized by force field minimization and molecular dynamics simulations (Fig. 1, B–D).
In the previously used two-angle model (40,41), the path of the linker DNA is characterized by an entry-exit angle α and a second angle β describing the torsion of the DNA between adjacent nucleosomes that are separated by a piece of linker DNA with length l (Fig. 2, A and B). However, evaluation of the high resolution structures in Fig. 1 revealed that additional degrees of freedom are needed to describe the geometry of the nucleosome accurately. Accordingly, two entry-exit angles α and γ are used to specify the path of the linker DNA in three dimensions (Fig. 2, A, D, and E) after leaving the chromatosome core particle. They are measured in two perpendicular planes, e.g., α in the plane parallel to the top and bottom of the nucleosome cylinder (Fig. 1, right panel) and γ in the plane defined by the dyad and parallel to the nucleosome cylinder axis (Fig. 1, left panel). Two more model parameters were introduced to mimic the binding of linker histone H1, which has ∼55 positive charges at pH 7.0, and is able to neutralize ∼27 bp of DNA flanking the 147 bp of the nucleosome core particle. In the coarse-grained model, the charged linker DNA entering or leaving the nucleosome is distinguished from the chromatosome core particle, which consists of the core histones, the linker histone H1, and the associated DNA of ∼170 bp. The charges of the chromatosome core particle are not considered explicitly. The position of H1 within the chromatosome is still under discussion and differs for the three model structures (Fig. 1, B–D). To account for these conformational variations in our model, the distance from the center of the histone core to the start of the charged linker DNA is described by a parameter c (Fig. 2, A and E). The gap between the two DNA strands leaving and entering the chromatosome core particle at this point is denoted by d (Fig. 2 C). Finally, the orientation of the chromatosome core particle relative to the linker DNA is characterized by three angles, φ, ɛ, and δ (Fig. 2, C–E). The angle φ permits a rotation of the chromatosome core particle about the axis perpendicular to the core dyad and to the vector d (Fig. 2, C and E). It can be used to model structures where the DNA is bent at the linker histone as for example in Fig. 1 B (left panel). The remaining two angles are defined as depicted in Fig. 2, C–E.
FIGURE 2.
Parameters describing the geometry of the nucleosomes in the six-angle model. (A–D) Nucleosome/chromatosome geometries as used in the MC simulation. Rotation angles of the depicted structures are φ = 0° (A), β = 90° (B), ɛ = 0° (C), and δ = 90° (D). (E) Schematic representation of the six-angle model in a top and side view. See text for details.
In summary, the geometry of the nucleosome is described by a set of six angles and three distances, where α, β, γ, l, and d define the conformation of the linker DNA, and δ, ɛ, φ, and c the distance and orientation of the nucleosome core particle relative to the linker DNA. The NRL can be computed as 147 bp + l (or 172 bp + l in the presence of H1). With this six-angle model, it is possible to translate the complex geometries observed in Fig. 1 into a coarse-grained model, which can then be used for MC simulations.
Calibration of the effective nucleosome-nucleosome interaction energy
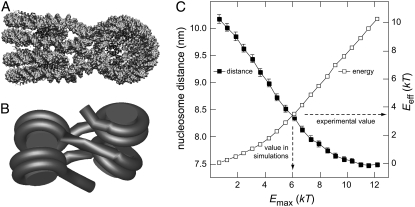
Although the energetics of DNA bending and twisting is the same as in Wedemann and Langowski (27), the interaction potential between nucleosomes was improved to fit the shape of nucleosomes better. The internucleosomal attraction energy was described by an oblate spherocylindrical potential (22,37) measured in units of kT (Boltzmann constant times absolute temperature T), which was parameterized by its maximum attraction energy Emax. The parameter set characterizing the potential is listed in Table S1, Data S1. From chromatin fiber stretching experiments, a value of 2.0 kcal mol−1 (3.4 kT at room temperature) was estimated for the disruption of nucleosome interactions (42). To calibrate the interaction potential, we examined the effect of energy variations on the stacking of two nucleosomes. For this purpose, the tetranucleosome structure (23) was rebuilt in terms of the coarse-grained six-angle model (Fig. 3). MC simulations with different values of Emax were conducted (Fig. 3 C) and the effective interaction energy Eeff was calculated from the fiber trajectories. In addition, the average distance between two interacting nucleosomes was determined. As expected, Eeff increased with Emax whereas the average nucleosome distance decreased (Fig. 3 C).
FIGURE 3.
Calibration of internucleosomal attraction energies. (A) Crystal structure of the tetranucleosome particle (23). Some bending of the linker DNA is induced to promote nucleosome-nucleosome stacking. (B) Coarse-grained model of the tetranucleosome used in the MC simulations. (C) Plot of mean nucleosome-nucleosome distance (▪) and mean effective internucleosomal attraction energy Eeff (□) versus the input value Emax. The parameter Emax is defined as the nucleosome-nucleosome interaction energy obtained for an optimal stacking of two nucleosomes. Data points represent averages of ∼1000 independent configurations with the error bars indicating the 95% confidence interval. An experimental value of Eeff = 3.4 kT was derived from chromatin stretching experiments (42). In the simulation, choosing Emax = 6.1 kT resulted in an effective interaction strength of Eeff = 3.5 kT. These values were used for all MC simulations of this study.
From the decrease of the average internucleosomal distance, it was deduced that Emax had to be larger than 5.5 kT to shift the equilibrium toward conformations that resembled the crystal structure (Fig. 3 B). A value of 6.1 kT was used for Emax for all chromatin fiber simulations in this study. The corresponding effective attraction energy was 3.5 kT, which at room temperature is very similar to the 2.0 kcal mol−1 measured in the chromatin fiber stretching experiments (42).
Investigating chromatin fiber models using the six-angle model of the nucleosome
Nucleosomes and chromatosomes were parameterized in terms of the six-angle model to investigate the formation of CL and ID chromatin fibers with chains of 100 nucleosomes in MC simulations. A central issue was the question if the different geometries would produce stable fiber structures at thermal equilibrium, and to which extent different NRLs could be accommodated. We therefore varied the NRL and adjusted the remaining parameters of the six-angle model to conserve the characteristics of the fiber model. The resulting structures were subjected to MC simulations to derive the distribution of fiber configurations at thermal equilibrium. This ensemble was then evaluated in terms of a set of parameters that included the geometric fiber shape as given by the FSC coefficient and the PCA ratio, the hydrodynamic shape described by the sedimentation and diffusion coefficient, and the fiber mass density, diameter, and persistence length (Tables 1, 2, and 3).
The first model investigated was based on the tetranucleosome x-ray structure (23). It represented a crossed-linker conformation forming a two-start helix without linker histone (Fig. 4 A). The NRL for this model was varied between 169 and 199 bp in steps of 10 bp whereas the entry-exit angles α and γ were chosen such that the nucleosomes were facing each other within the helix (see Table 1, and Fig. S2, Data S1). The remaining parameters were fixed at β = 140°, ɛ = 0°, φ = 0°, c = 3.3 nm, and d = 8 nm.
FIGURE 4.
MC configurations of the CL, ID20, and ID40+ nucleosome chain geometries. Chains of 100 nucleosomes/chromatosomes used in the MC simulations are presented. The first two rows show side and top views of the initial structures with relaxed DNA bend, stretch, and torsion potentials. They represent different local nucleosome/chromatosome geometries optimal for the formation of CL and ID fibers. The last row displays representative configurations from the MC simulations after reaching thermal equilibrium. (A) CL fiber with NRL = 169 bp. In the course of the MC simulation, the mass density was reduced to 3.1 ± 0.1 nucleosomes/11 nm fiber length as compared to the start conformation, which had a value of 5.5 nucleosomes/11 nm fiber (Table 1). It is noted that the initial fiber shape is preserved. (B) ID20 chain with NRL = 197 bp. The initial fiber shape is lost during the MC run. (C) ID40+ fiber with NRL = 187 bp. The compacted interdigitated fiber conformation with 5.8 nucleosomes per turn and a nucleosome tilt angle of ∼60° is maintained. The average mass density of this structure drops from 10.7 nucleosomes/11 nm fiber length in the start structure to 7.6 ± 0.2 nucleosomes/11 nm fiber in the equilibrium ensemble (Table 3).
TABLE 1.
Two-start helix crossed-linker fiber conformation (CL)
| NRL (bp) | α (°) | γ (°) | FSC | PCA ratio | Sedimentation coefficient (S) | Diffusion coefficient (× 10−8 cm2s−1) | Fiber mass density (Nucleosomes/11 nm fiber) | Fiber diameter (nm) | Persistence length (nm) |
|---|---|---|---|---|---|---|---|---|---|
| 169 | 50 | −50 | 0.97 ± 0.07 | 5.7 ± 2.4 | 154 ± 14 | 4.4 ± 0.4 | 3.1 ± 0.1 | 30.8 ± 0.3 | 51 ± 34 |
| 179 | 35 | −35 | 0.90 ± 0.11 | 4.5 ± 1.9 | 155 ± 16 | 4.2 ± 0.4 | 2.8 ± 0.1 | 32.8 ± 0.3 | 33 ± 25 |
| 189 | 27 | −27 | 0.83 ± 0.14 | 3.8 ± 1.5 | 156 ± 17 | 4.0 ± 0.4 | 2.4 ± 0.1 | 34.7 ± 0.3 | 25 ± 19 |
| 199 | 22 | −22 | 0.80 ± 0.12 | 3.4 ± 1.3 | 155 ± 15 | 3.7 ± 0.4 | 2.2 ± 0.1 | 36.5 ± 0.3 | 22 ± 16 |
Simulations were conducted with the following parameters: 100 nucleosomes, β = 140°, δ = 20°, φ = 0°, ɛ = 0°, c = 3.3 nm, d = 8 nm, and Emax = 6.1 kT.
The second structure resembled the model of an interdigitated one-start helix conformation, which was developed from electron microscopy studies of in vitro reconstituted nucleosome arrays containing one linker histone per nucleosome (24). This model is characterized by a relatively small nucleosome tilt angle of ∼20° and high mass densities of up to 11–15 nucleosomes/11 nm, and is designated as ID20 fiber here. For the original model, the path of the linker DNA has not been defined. Accordingly, several conformations of the DNA path were tested with the six-angle model. The nucleosome positions were best preserved with an entry-exit angle of α = −114° and the distance c = 6.0 nm. To maintain the interdigitation of nucleosomes from adjacent gyres at different repeat lengths between 187 and 237 bp, the entry-exit angle γ had to be adapted (see Table 2, and Fig. S3, Data S1). The other parameters remained fixed at β = 0°, ɛ = 0°, φ = 0°, and d = 3.7 nm. This geometry resulted in a number of 5.5 nucleosomes per helical turn and a mass density of ∼9 nucleosomes/11 nm fiber (see Fig. 4 B, and Fig. S3, Data S1).
TABLE 2.
Interdigitated one-start helix fibers with low nucleosome tilt (ID20)
| NRL (bp) | γ (°) | FSC | PCA ratio | Sedimentation coefficient (S) | Diffusion coefficient (× 10−8 cm2s−1) | Fiber mass density (Nucleosomes/11 nm fiber) | Fiber diameter (nm) | Persistence length (nm) |
|---|---|---|---|---|---|---|---|---|
| 187 | −60 | 0.92 ± 0.08 | 3.5 ± 1.4 | 189 ± 19 | 5.2 ± 0.5 | 4.2 ± 0.3 | 34.9 ± 0.4 | 21 ± 17 |
| 197 | −37 | 0.77 ± 0.09 | 2.7 ± 1.0 | 186 ± 18 | 4.9 ± 0.5 | — | — | — |
| 207 | −26 | 0.59 ± 0.06 | 1.8 ± 0.4 | 204 ± 12 | 5.2 ± 0.3 | — | — | — |
| 217 | −20 | 0.55 ± 0.09 | 1.9 ± 0.6 | 168 ± 10 | 4.2 ± 0.3 | — | — | — |
| 227 | −17 | 0.60 ± 0.11 | 2.4 ± 0.8 | 147 ± 13 | 3.5 ± 0.3 | — | — | — |
| 237 | −14 | 0.70 ± 0.11 | 3.0 ± 1.0 | 123 ± 12 | 2.9 ± 0.3 | — | — | — |
Simulations were conducted with the following parameters: 100 nucleosomes, 5.5 nucleosomes per turn, α = −114°, β = 0°, δ = 20°, φ = 0°, ɛ = 0°, c = 6.0 nm, d = 3.7 nm, Emax = 6.1 kT.
Finally, we examined a family of fiber models with interdigitated nucleosome helices proposed by Daban (25). These models had higher tilt angles than the ID20 conformation between 40° and 60° and were therefore termed ID40+ fibers. Nucleosomes from different helical turns face each other to form secondary helices (Fig. 4 C). The nucleosome tilt angle varies with the number of secondary helices or the number of nucleosomes per turn. Four different subfamilies with 3.8, 4.7, 5.8, and 6.8 nucleosomes per turn were analyzed, and for each of them, the NRL was varied from 187 to 207 bp (see Table 3, and Figs. S4 and S5, Data S1). The entry-exit angles of the DNA were chosen to accommodate the different number of nucleosomes per turn and the varying NRL. Furthermore, the tilt angle δ had to be adapted to ensure that the nucleosomes face each other within the secondary helices. The remaining parameters were constant at β = 0°, ɛ = 0°, φ = 0°, c = 5.6 nm, and d = 3.7 nm. For both the CL and ID conformations a symmetric conformation of the nucleosome with angles ɛ = φ = 0° was used. However, it is noted that asymmetric conformations such as those depicted in Fig. 1, B and C, can be mimicked by adjusting these angles to appropriate values.
TABLE 3.
Interdigitated one-start helix fibers with high nucleosome tilt angle (ID40+)
| NRL (bp) | α (°) | δ (°) | γ (°) | Nucleosomes per turn | FSC | PCA ratio | Sedimentation coefficient (S) | Diffusion coefficient (× 10−8 cm2s−1) | Fiber mass density (Nucleosomes/11 nm fiber) | Fiber diameter (nm) | Persistence length (nm) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 187 | 84 | 60 | −55 | 3.8 | 1.00 ± 0.00 | 6.4 ± 1.0 | 204 ± 4 | 5.6 ± 0.1 | 5.9 ± 0.2 | 32.0 ± 0.2 | 131 ± 67 |
| 187 | 104 | 60 | −60 | 4.7 | 1.00 ± 0.00 | 6.3 ± 0.4 | 217 ± 3 | 6.0 ± 0.1 | 6.6 ± 0.2 | 32.2 ± 0.1 | 231 ± 109 |
| 187 | 118 | 60 | −65 | 5.8 | 1.00 ± 0.00 | 5.5 ± 0.2 | 230 ± 3 | 6.3 ± 0.1 | 7.6 ± 0.2 | 32.8 ± 0.1 | 381 ± 192 |
| 187 | 127 | 60 | −65 | 6.8 | 1.00 ± 0.00 | 5.2 ± 0.2 | 233 ± 2 | 6.4 ± 0.1 | 7.9 ± 0.2 | 33.0 ± 0.1 | 390 ± 201 |
| 197 | 84 | 45 | −35 | 3.8 | 0.90 ± 0.04 | 2.1 ± 0.7 | 221 ± 10 | 5.9 ± 0.3 | — | — | — |
| 197 | 104 | 50 | −37 | 4.7 | 0.95 ± 0.03 | 3.4 ± 1.1 | 207 ± 13 | 5.5 ± 0.3 | 5.6 ± 0.3 | 35.3 ± 0.3 | 26 ± 20 |
| 197 | 118 | 58 | −39 | 5.8 | 0.92 ± 0.04 | 3.5 ± 0.7 | 214 ± 8 | 5.7 ± 0.2 | 6.9 ± 0.5 | 36.2 ± 0.4 | 50 ± 29 |
| 197 | 127 | 60 | −40 | 6.8 | 0.88 ± 0.04 | 3.2 ± 0.4 | 221 ± 7 | 5.8 ± 0.2 | 7.3 ± 0.5 | 36.8 ± 0.3 | 52 ± 23 |
| 207 | 84 | 40 | −26 | 3.8 | 0.71 ± 0.03 | 2.3 ± 0.4 | 203 ± 6 | 5.2 ± 0.1 | — | — | — |
| 207 | 104 | 40 | −28 | 4.7 | 0.70 ± 0.05 | 2.0 ± 0.4 | 204 ± 8 | 5.2 ± 0.2 | — | — | — |
| 207 | 118 | 52 | −28 | 5.8 | 0.63 ± 0.07 | 1.9 ± 0.4 | 201 ± 8 | 5.1 ± 0.2 | — | — | — |
| 207 | 127 | 48 | −30 | 6.8 | 0.57 ± 0.06 | 2.0 ± 0.4 | 202 ± 11 | 5.1 ± 0.3 | — | — | — |
Simulations were conducted with the following parameters: 100 nucleosomes, β = 0°, φ = 0°, ɛ = 0°, c = 5.6 nm, d = 3.7 nm, Emax = 6.1 kT.
Variations of the linker DNA twist angle induce large changes of the fiber conformation
A systematic screening of the complete parameter space by MC simulations is a challenging task because of the high dimensionality of the six-angle model. Accordingly, the CL and ID conformations were used as starting points to investigate the influence of a selected set of parameters. An example for this type of analysis is shown in Fig. 5 for CL fibers and ID40+ fiber conformations based on the structures listed in Tables 1 and 3. For both structures, the entry-exit angle α and the length l of the linker DNA were systematically changed. The DNA tilt angle β was increased by 36° for every basepair added. This twist of the DNA induced a rotation of the nucleosomes. For the CL and ID40+ structures studied here, the favorable stacking of nucleosomes was preserved for ∼10 bp increments of the linker DNA (corresponding to rotations of 360°), albeit with a decrease of the mass density for higher linker lengths (Fig. 5, A–C). It is also apparent that the ID40+ fibers have a significantly higher mass density of up to ∼8 nucleosomes per 11 nm fiber length as compared to 2–3 for the CL conformation (Fig. 5 D). Due to the different geometries of the DNA at the nucleosome, the mass densities of the CL and ID fibers did not peak at the same value of the NRL (Fig. 5 C). The parameter screen illustrated how small changes in the NRL can induce large changes of the chromatin fiber conformation. The influence of changes to the angle α was moderate and resulted in a linear change of the mass density.
FIGURE 5.
Dependence of the mass density on the local nucleosome/chromatosome geometry. The conformation of CL and ID40+ fibers was investigated for entry-exit angles α in steps of 2.5° and NRLs varied in one-basepair intervals. (A) CL fiber conformations were simulated for entry-exit angles α between 20° and 50°, NRLs ranging from 168 to 200 bp, and fixed values of γ = −35°, δ = 20°, ɛ = 0°, φ = 0°, c = 3.3 nm, and d = 8.0 nm. The value of β was increased by 36° for each basepair added, starting from a value of β = 184° at an NRL of 168 bp. (B) ID40+ conformations were screened in the range of α = 80–130°, NRLs = 181–220 bp, and fixed values of γ = −39°, δ = 58°, ɛ = 0°, φ = 0°, c = 5.6 nm, and d = 3.7 nm. The value of β was augmented by 36° per basepair added to the smallest NRL of 181 bp, for which β = 144° was used. (C) Comparison between CL fibers at α = 35° and ID fibers at α = 117.5°. It is apparent that the mass densities of the CL fibers are significantly lower than those of the ID fibers. The numbers 1–3 refer to the conformations shown in D. (D) Configurations from C to illustrate the observed fluctuations in mass density for α = 117.5° and NRLs of 186 bp (1), 191 bp (2), and 197 bp (3).
Fibers based on the tetranucleosome structure
The conformation of nucleosome arrays with CL geometry was determined after equilibrating the fibers at room temperature using MC simulations. Structures with a NRL of 169 bp formed stable fibers (Fig. 4 A), illustrated by a high FSC value of 0.97 ± 0.07 (see Table 1). The high PCA ratio showed that such fibers adopted a long, outstretched conformation. However, as indicated by the large standard deviation of the PCA ratio, the fiber shape fluctuated due to bending. This observation was confirmed by the relatively low persistence length of ∼50 nm, which was only ∼1/6 of the length of the fiber backbone. Because of the outstretched conformation of these fibers, the sedimentation and diffusion coefficients were low compared to ID40+ structures (see Tables 1 and 3).
Increasing the NRL up to 199 bp (Fig. S2, Data S1) reduced the FSC value, the PCA ratio, and the diffusion coefficient, whereas the sedimentation coefficients remained constant at ∼155 S. The CL geometries with larger NRLs formed stable fibers, yet they were more flexible and adopted a more open conformation, which was also reflected by a decrease of the mass density from 3.1 nucleosomes per 11 nm for 169 bp NRL down to 2.2 nucleosomes per 11 nm for 199 bp. Since the linker DNA crossed the fiber center in the CL geometries, the average fiber diameter increased with the NRL from 30.8 ± 0.3 nm to 36.5 ± 0.3 nm (see Table 1).
Reorganization of ID fibers with small nucleosome tilt angles at thermal equilibrium
In the MC simulations, the propensity of the appropriate chromatosome conformations to form fibers in an ID20 conformation was examined for a series of NRLs with the indicated path of the linker DNA (Fig. 4 B; Fig. S3, Data S1). Only with an NRL of 187 bp was a fiber-shaped structure (FSC = 0.92 ± 0.08, PCA ratio = 3.5 ± 1.4) formed with a relatively low mass density of 4.2 ± 0.3 nucleosomes/11 nm. The large standard deviations of these values reflect fluctuations of the fiber shape. For longer NRLs, our criteria for a fiber shape (FSC ≥ 0.8, PCA ratio ≥ 3) were not fulfilled (Table 2). The largest deviations from the fiber shape were obtained with an NRL of 217 bp (FSC = 0.55 ± 0.09, PCA ratio = 1.9 ± 0.6) indicating that aggregated structures rather than fibers were formed (Table 2). For NRLs > 217 bp, the FSC value and the PCA ratio increased again, which reflected the formation of more open and extended structures.
When examining the geometry of the fiber conformation obtained at an NRL of 187 bp, it became apparent that the initial ID20 conformation changed into an open solenoidal shape, which was no longer interdigitated (Fig. S3 A, Data S1). This transition can be rationalized by the tendency of the cylindrical nucleosomes to stack on top of each other to maximize the interaction surface. This is the energetically most favorable geometry for the nucleosome interaction potential used here. In contrast, in the ID20 start conformation, the nucleosome displays only a partial overlap of the interaction surface. Thus, the MC simulations suggest that the ID20 conformation proposed previously is not observed at thermal equilibrium for the parameter set used here.
Stabilizing the ID fiber conformation by increasing the local nucleosome tilt angle
The stability of the interdigitated one-start helix fibers was largely increased by changing the tilt of the nucleosomes to 40–60°. It resulted in conformations similar to those proposed by Daban (25) that are referred to as ID40+ fibers. The higher tilt angle facilitated an aligned stacking of the nucleosomes, which is the most favorable arrangement of the interaction potential used. For each NRL, several structures could be constructed that varied with respect to the number of nucleosomes per turn (Fig. S5, Data S1). All structures with NRLs of 187 bp (Fig. 4 C, with 5.8 nucleosomes per turn) had an FSC value of 1.0. Furthermore, the PCA ratios, the sedimentation and diffusion coefficients, and the persistence length had the highest values of all simulated fiber models and a low standard deviation (Table 3).
Increasing the NRL decreased the fiber stability, and the fraction of configurations with an aggregated structure was augmented. Although the ID40+ fiber conformation was maintained at thermal equilibrium for NRL = 197 bp (FSC ∼ 0.9, PCA ratio ∼ 3.3), the fraction of more globular configuration was higher than with an NRL of 187 bp (Fig. S4, A and B, Data S1). This increase in conformational flexibility was also reflected in a large reduction of the persistence length to ∼50 nm. The mass density for NRL = 197 bp and more than 4 nucleosomes per turn reached 7.3 nucleosomes/11 nm, compared to 7.9 nucleosomes/11 nm for 187 bp NRL. With NRL values of 207 bp and above, no fiber structure was formed as indicated by FSC values below 0.8 and PCA values below 2 (Fig. S4 C, Data S1; and Table 3).
DISCUSSION
In this study, the relation between the local geometry of the nucleosome and the conformation of the chromatin fiber was examined. The packaging of DNA into the chromatin fiber and its higher order folding has long been recognized as a mechanism to control the accessibility of the DNA during transcription, replication, recombination, and DNA repair (2–4). To address this point, a coarse-grained model of the nucleosome and chromatosome was derived from molecular modeling and energy minimization. The available model structures for the complex of the linker histone at the nucleosome are based mostly on possible interactions of the isolated gH5 domain (43). The gH5-DNA interaction was homology modeled to the DNA cocrystal structure of the transcription factor HNF3 that has a winged helix DNA binding motif with a recognition α-helix positioned in the major groove of the DNA (17,44,45). However, a systematic computational docking analysis revealed several other possible orientations for the interaction of gH5 with the nucleosome (19). In addition, the C-terminal domain of H1/H5 represents an additional DNA binding module (46,47), for which a homology-based model structure from Bharath et al. (45) was used here. Thus, a considerable uncertainty exists with respect to the chromatosome structure.
The models depicted in Fig. 1 have been considered to define the conformational space of the DNA geometry. From inspection of the four structures, it becomes apparent that the path of the linker DNA varied significantly. This is accounted for by the description of the local nucleosome/chromatosome geometry according to the six-angle model (Fig. 2). Previous MC simulations (26,27,29,30) were mostly based on the two-angle model (40,41), which restricts the conformational space considerably. Its inability to reproduce the chromatosome structures for simulations of ID fibers has been discussed above, and it is not suited for a representation of the CL fiber conformation either. The original two-angle model requires that the paths of the incoming and outgoing linker DNA originate from the same point at the histone octamer (40), which is clearly not the case (Fig. 1 A). In addition, such a conformation implies a twofold wrapping of the DNA, i.e., an NRL of at least 177 bp. The two-angle model was extended previously by the distance d between the two DNA strands as an additional parameter (Fig. 2, C and E) (27), However, in the absence of the new angle δ introduced here, d would always be oriented parallel to the nucleosome cylinder axis as shown in Fig. 2 E. Thus, the angle δ is essential to describe the nucleosome tilt angle to the fiber axis in the ID conformation as well as the correct positioning of the DNA entry-exit points in the CL conformations. In general, to describe the position and orientation of any object in three-dimensional space, six parameters are needed. To determine the nucleosome position relative to the linker DNA, five parameters are sufficient because of the cylindrical symmetry of the nucleosome in the coarse-grained model. Furthermore, translations along the cylinder axis (i.e., parallel to d in Fig. 2 E) were not considered here since they were not needed to represent the model structures in Fig. 1. This reduced the number of parameters for the nucleosome to four (three angles, δ, ɛ, and φ; and one distance, c). To describe the trajectory of the linker DNA, the angles α, β, and γ and the distances l and d are needed (Fig. 2), which lead to a total of six angles and three distances for our coarse-grained model. It is noted that the simulations of the CL and ID structures were conducted here with ɛ = 0°, φ = 0°, i.e., with a parameter set of four angles and three distances. However, the two additional angles, ɛ and φ, would be required to represent the asymmetric topology in nucleosome/chromatosome structures like those depicted in Fig. 1, B and C. Therefore, they have been included in our model to provide a complete description of the local nucleosome geometry.
An advanced mesoscopic model of oligonucleosomes has been developed by Schlick and co-workers to describe the conformational freedom and electrostatics of the nucleosome, including the histone tails (28,48). Due to its more detailed description of the nucleosome electrostatics in a so-called discrete surface-charge optimization model (DiSCO), the simulations are computationally expensive. Accordingly, the applications reported so far have focused on oligonucleosome structures containing 6–48 nucleosomes. It is noteworthy that this modeling approach has been successful in displaying the salt-dependent compaction of 12 unit oligonucleosomes (28) as well as the prominent role of the H4 tail in mediating internucleosomal interactions (48). These are specific chromatin features inferred from experiments that are not reproduced by more coarse-grained models, including our own. In terms of an analysis of the relation between nucleosome geometry and chromatin fiber conformation, no systematic study has been reported for the DiSCO mesoscopic model, and the potential effect of linker histone binding has not been evaluated. The 24 and 48 nucleosome chains display fiber-like shapes with a flexible zig-zag arrangement of nucleosomes when investigated with the DiSCO model (48). The conformation bears some similarities to the two-start helix CL conformation described here, but is significantly more irregular.
Fiber shape analysis
A central issue for the evaluation of MC trajectories is the question if they represent a stable fiber conformation or if other shapes are favored. This issue was addressed by using a combination of two parameters: the computation of FSC and PCA. The FSC value is inversely proportional to the degree of nucleosome intermingling between distant regions of the chromatin fiber (22). For the structures examined here, a value ≥0.8 was indicative of a fiber-like conformation. In addition, the global shape of the trajectory was described by the ratio of the longest and shortest axis of an ellipsoid from the PCA analysis. From the evaluation of the MC trajectories, it was concluded that a PCA long/short axis ratio ≥3 corresponded to a fiber-shaped structure. Using these criteria, the CL fiber conformations listed in Table 1, the ID20 structure with an NRL of 187 bp and the ID40+ conformations with 187 and 197 bp and more than four nucleosomes per turn would be classified as fibers. It is noted that the ID20 start structure with 187 bp NRL rearranges into a different structure in the MC simulations (Fig. S3 A, Data S1), in which the nucleosome stacking is aligned and no longer interdigitated. This reflects the geometry of the nucleosome-nucleosome interaction potential used here, for which the most favorable conformation is the stacking of nucleosome cylinders on top of each other.
Sedimentation and diffusion coefficients
Sedimentation and diffusion coefficients were computed from the trajectories to characterize the hydrodynamic shape of the nucleosome chains. For macromolecules with constant mass, the sedimentation coefficient s is highest if the molecule forms a compact sphere, and decreases if the shape changes to a rod or a random coil. It is also proportional to the mass of the particle (Eq. 1), which increases somewhat with the NRL and/or the incorporation of linker histone H1. A relatively low s value cannot be directly related to a fiber shape as it can result not only from a rod-like conformation but also from a random coil. In addition, compact fibers with large diameters and high mass densities could exhibit relatively high s values although their shape is clearly not spherical. The same relation (compact sphere > rod/random coil) applies to the diffusion coefficient, which can be directly related to the friction coefficient f according to Eq. 1. Despite the complex relation of s and D values with the fiber shape, these parameters have the advantage that they can be directly compared to experimental measurements that cover chain lengths from 2 to 60 nucleosomes determined for samples from rat liver nuclei (49,50), chicken erythrocytes (51), nuclei from bovine thymus (52), and HeLa cells (15). The expected dependence of the sedimentation coefficient s on the molecular weight M of the fiber is s ∝ ln M for short rod-like shapes and s ∝ M1/2 for longer chains that are in a worm-like coil conformation. This behavior can be approximated with the relation s = c1 × M1/2 + c2 derived previously for DNA with deviations of the exponent from 1/2 reflecting excluded-volume effects (53,54). Accordingly, we used the function 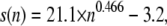 with n being the number of nucleosomes to extrapolate a sedimentation coefficient of ∼180 S for a chromatin fiber of 100 nucleosomes with NRL = 200 bp and an ionic strength of 0.1 M from the experimental data (Fig. S6, Data S1). The corresponding value for the diffusion coefficient would be D = 5.1 × 10−8 cm2 s−1 as computed from Eq. 2 with a fiber mass of 26.5 MDa (including H1). This compares to s = 155 ± 15 S and D = (3.7 ± 0.4) × 10−8 cm2 s−1 for the CL and s = 215 ± 10 S and D = (5.7 ± 0.3) × 10−8 cm2 s−1 for the ID40+ fiber with 199 and 197 bp NRLs respectively (Tables 1 and 3). In this context, it is noteworthy that both the tetranucleosome structure by Schalch et al. (23) and the electron microscopy (EM) work by Robinson et al. (24) use repeats of the strong 601 nucleosome positioning sequence with constant linker DNA length. This leads to an NRL that is, as in our models, exactly the same throughout the chain. Irregularities in nucleosome positioning around an average NRL value as expected for natural DNA sequences are likely to result in a less compacted fiber conformation. Thus, for the structures analyzed here, the hydrodynamic shape parameters would fit best to a somewhat decondensed ID40+ fiber conformation, in which, due to NRL variations, the sedimentation and diffusion coefficients are reduced as compared to the data retrieved from the MC simulations.
with n being the number of nucleosomes to extrapolate a sedimentation coefficient of ∼180 S for a chromatin fiber of 100 nucleosomes with NRL = 200 bp and an ionic strength of 0.1 M from the experimental data (Fig. S6, Data S1). The corresponding value for the diffusion coefficient would be D = 5.1 × 10−8 cm2 s−1 as computed from Eq. 2 with a fiber mass of 26.5 MDa (including H1). This compares to s = 155 ± 15 S and D = (3.7 ± 0.4) × 10−8 cm2 s−1 for the CL and s = 215 ± 10 S and D = (5.7 ± 0.3) × 10−8 cm2 s−1 for the ID40+ fiber with 199 and 197 bp NRLs respectively (Tables 1 and 3). In this context, it is noteworthy that both the tetranucleosome structure by Schalch et al. (23) and the electron microscopy (EM) work by Robinson et al. (24) use repeats of the strong 601 nucleosome positioning sequence with constant linker DNA length. This leads to an NRL that is, as in our models, exactly the same throughout the chain. Irregularities in nucleosome positioning around an average NRL value as expected for natural DNA sequences are likely to result in a less compacted fiber conformation. Thus, for the structures analyzed here, the hydrodynamic shape parameters would fit best to a somewhat decondensed ID40+ fiber conformation, in which, due to NRL variations, the sedimentation and diffusion coefficients are reduced as compared to the data retrieved from the MC simulations.
Fibers with crossed-linker DNA
The analysis mentioned above indicated that the CL structures adopted a fiber shape. However, the mass densities of CL fibers are relatively low at 2.2–3.1 nucleosomes per 11 nm fiber length (Table 1). This is significantly smaller than the value of 5.5 nucleosomes per 11 nm that would be obtained by simply extending the crystal structure (23). Thus, the MC simulations suggest that the tetranucleosome conformation is indeed compatible with a fiber structure, but the average conformation in solution is expected to be significantly more open than the tight packaging observed in the crystal. The relatively extended structure of the CL fibers is also apparent from the calculated values of the sedimentation coefficient, which were found to be independent of the repeat length with an average value of 155 ± 1 S (Table 1). Both the s value as well as the corresponding diffusion coefficient of ∼4 × 10−8 cm2s−1 are significantly lower than the above estimates for a native chromatin fiber fragment of 100 nucleosomes, supporting the view that the CL conformation represents a very open chromatin fiber structure.
It is noted that the tetranucleosome crystal structure has been obtained with an NRL of 169 bp. Due to steric constraints, it appears to be impossible to include linker histones bound to each of the four nucleosome particles in this structure. This is consistent with the experimental finding that nucleosomes saturated with H1 are observed only for longer NRLs. For example, a stoichiometry of 0.45 linker histone per nucleosome was found in neuronal chromatin with a repeat length of 162 bp, whereas a value of 1.04 was determined for chromatin in glial cells that had a repeat length of 204 bp (55). A similar relationship of linker histone content and NRL was derived from an analysis in different mouse tissues (56,57). Thus, the CL fiber conformation appears to be favorable for chains with short NRLs in the absence of linker histones. This requirement is at least partially fulfilled for yeast chromatin where a linker histone homolog is missing and the NRL is ∼165 bp (1). It can be speculated that under these conditions, a CL-like chromatin fiber structure forms. According to the results obtained in the MC simulations, NRLs of ∼188 bp and ∼196 bp, which are the two most frequently found values in higher eukaryotes (1,6), would be decondensed in the CL fiber conformation. The structure is more “open” and most of the linker DNA is accessible. As discussed previously, a disruption of a compact chromatin fiber structure would increase the propensity of the core histone H2A·H2B dimer to dissociate from the nucleosome core particle, which appears to be essential for the translocation of RNA polymerase through chromatin (4,58). In vivo, the dissociation of linker histone H1 could be induced by its binding to a histone chaperone-like NAP1 (15), and/or the competition of linker histone and HMGN proteins to a binding site at the nucleosome (59).
Fibers with interdigitated nucleosomes
Fibers with ID geometries represent nucleosome chains with bound linker histones. The linker histone has two important effects: First, it can change the path of the DNA, including bending of the linker DNA. Second, its high positive charge of ∼+55 neutralizes negative charges of the linker DNA backbone. Thus, it appears unlikely that compact solenoidal fiber structures with bent linker DNA could form in the absence of linker histones, since the linker DNA is likely to be straight in this case (60). For the ID40+ structures evaluated here we found average mass densities of up to eight nucleosomes/11 nm fiber and nine nucleosomes/11 nm for some even more compacted configurations. It is noted that the nucleosome interactions depend strongly on their relative orientation to each other. The cylindrical potential used here disfavors the formation of nucleosome aggregates that are observed with spherical or ellipsoidal potentials as discussed in detail elsewhere (22). Experimental values for the fiber mass density have been determined by various techniques, and the consensus estimate for native chromatin fibers is 6–7 nucleosomes/11 nm fiber length ((1,61) and references therein). More recently, high mass densities have been found for chromatin fibers reconstituted with 50–70 copies of high affinity binding sites in the presence of 1.0–1.6 mM MgCl2 and one linker histone H5 per nucleosome (24). Under these conditions, the mass density reaches 10–11 nucleosomes/11 nm fiber for NRLs of up to 207 bp and even ∼15 nucleosomes/11 nm for longer NRLs. Although these values might include some bias toward a selection of fully compacted structures on the images, they clearly represent a new upper limit for the chromatin fiber mass density that was not apparent from the analysis of native chromatin fiber fragments averaged over different sequences.
Thus, in terms of the compaction of the chromatin fiber, the best agreement between the MC simulations and the above EM data is obtained with the ID40+ conformation. It is noted that its characteristic feature, the high tilt angle of the nucleosomes to the fiber axis, is in agreement with optical anisotropy studies where nucleosome tilt angles between 45° and 60° have been determined (62,63). However, such a conformation is challenged by the EM image analysis that suggests a ∼20° tilt angle with an almost parallel orientation of the nucleosomes to the fiber axis (21,24).
Linker length, persistence length and fiber diameter
In all simulated fiber geometries, an increase of the nucleosome repeat length destabilized the fiber conformation (Tables 1–3; Figs. S2–S4, Data S1). The effect was most pronounced for the ID20 conformations, where chains with NRLs > 187 bp did not adopt a fiber shaped conformation according to the criteria discussed above. The destabilizing effect of the linker DNA can be explained by the increase of electrostatic repulsion. One parameter that could counteract this effect would be an increase of the nucleosome interaction energy. As reported in the context of Fig. 3, the nucleosome stacking interaction was chosen to reproduce an effective interaction of Eeff = 3.4 kT, as derived from stretching experiments of single chromatin fibers (42). This value is in agreement with the analysis of the tetranucleosome conformation in dependence of the nucleosome-nucleosome interaction strength conducted here. However, higher values would also be compatible with these simulations. An additional contribution that has not been considered in the MC simulations could come from interactions among neighboring linker histones. It has been demonstrated that H1 binds cooperatively to DNA, which points to the existence of protein-protein interactions in its DNA complex (64,65). These could contribute to further compaction of the ID structures and stabilize the fiber for larger NRLs.
The persistence length P of the chromatin fiber displayed large variations with values between 22 and 390 nm (Tables 1–3). This correlates with the range of 30–220 nm determined experimentally as reviewed by Rippe (39). In agreement with MC simulations of other chromatin fiber conformations reported by Aumann et al. (30), an increase of the NRL caused a decrease of the persistence length for both CL and ID conformations. The high flexibility of the CL fiber (P = 22–51 nm), which resembles yeast chromatin in some aspects, is in agreement with a persistence length of ∼30 nm derived from in situ cross-linking experiments (66). ID40+ fibers were much stiffer with P = 390 nm for an NRL of 187 bp.
The computed fiber diameter of 30–37 nm for NRLs up to 199 bp is very similar to previously reported values ((21,24) and references therein). Within the limited data set of fiber-shaped structures, it increased continuously with the repeat length. The formation of two distinct structural classes of ID fibers with different diameter and mass density as observed in the experiments could not be explained with our model structures, as no stable fibers formed for NRLs above 197 bp. In Robinson et al. (24), a diameter of 33–34 nm was measured for NRLs of 177–207 bp, whereas chains with longer NRLs of 217–237 bp associated into thicker fibers with a diameter of 43 nm. The transition of the fiber conformation between 207 and 217 bp repeat length can be explained by an increase of the nucleosome number per turn, which suggests a change in the organization of the linker DNA. This is likely to be required to reestablish favorable nucleosome-nucleosome interactions, but the underlying conformational changes remain to be elucidated.
Relation of fiber mass density with the helical twist of DNA
The relation of the twist angle between adjacent nucleosomes and the linker DNA length is defined by the helical DNA twist of ∼36° per basepair. The influence of this parameter on the fiber mass density was studied by systematic variations of the linker DNA length in one-basepair steps in conjunction with changes in the entry-exit angle α (Fig. 5). The peaks of the mass density were found at NRLs of 170 bp, 180 bp, and 191 bp for the CL fibers and at 186 bp, 197 bp, 207 bp, and 217 bp for the ID40+ geometry. The results demonstrate a clear dependence on the ∼10 bp periodicity of the DNA helix, in excellent agreement with a previous analysis of the distribution of naturally found NRLs (6). Furthermore, three additional important conclusions can be made. First, the peaks of the ID40+ fibers are relatively narrow with large differences between maxima and minima. This suggests that the fiber mass density is highly dependent on the local nucleosome geometry and that it could be modulated by factors that induce variations in the DNA twist. Second, the two curves do not display overlaps of the peak positions but rather a shift of 5 bp. The relevance of this finding needs to be examined in further simulations, in which atomic resolution modeling is conducted to assess whether this effect is real or results from an inaccuracy of the coarse-grained model. Third, the results confirm the decondensation of the chromatin fiber with increasing NRLs that has been discussed above.
CONCLUSIONS
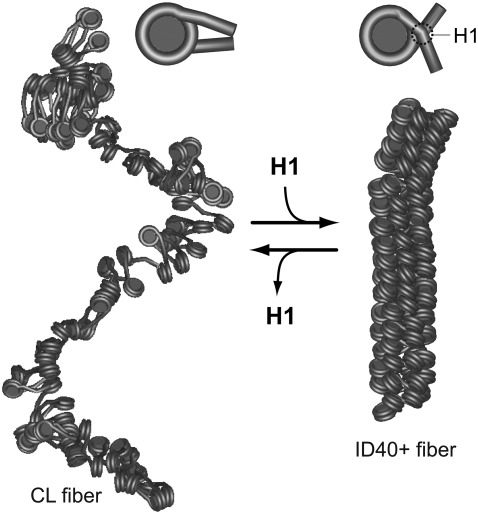
It is apparent from the results obtained here that the geometry of the DNA at the nucleosome/chromatosome is polymorphic, and that local variations can translate into large changes of the chromatin fiber conformation. By combining atomic scale modeling and energy minimizations of single nucleosomes/chromatosomes with coarse-graining, the conformational changes of chromatin fibers were analyzed by MC simulations. From the resulting ensembles of different fiber types at thermal equilibrium, a detailed structural framework for the reorganization of chromatin in response to binding of linker histone H1 is obtained leading to the model depicted in Fig. 6. In the absence of linker histone, an open CL fiber conformation is present. This structure preserves a local nucleosome geometry similar to that of the tetranucleosome crystal structure if the NRL is extended to ∼189 bp, with most of the linker DNA being easily accessible. Upon binding of linker histone H1, a chromatosome conformation is induced that closely resembles a structure proposed previously (17). This change of the local DNA geometry induces a strong compaction into an ID fiber conformation that occludes the linker DNA by bringing it inside the compact fiber structure.
FIGURE 6.
Model for chromatin fiber compaction induced by binding of linker histone H1. The CL fiber (left), without linker histone, represents an open conformation with straight linker DNA, in which DNA access is facilitated for other proteins. The binding of linker histone H1 changes the local nucleosome geometry to a structure similar to the one proposed in Fig. 1 C with partial DNA charge neutralization (right). This induces a transition to an ID fiber conformation. The structures shown have an NRL of ∼188 bp in both the CL fiber (left side) and the ID40+ conformation (right side), and are taken from the MC simulations. The mass density of the CL fiber is ∼40% of the mass density of the ID40+ fiber (Tables 1 and 3).
Thus, the use of numerical simulations can provide valuable insights for identifying parameters that determine the conformation of the chromatin fiber. For a more accurate prediction of its dynamic organization, additional experimental data in three areas are required:
A high resolution structure of the chromatosome as the basic building block of chromatin with bound linker histones is needed that could be parameterized into a coarse-grained model along the lines developed here.
The strength of the nucleosome-nucleosome interaction and its dependence on the nucleosome-nucleosome orientation have to be determined more precisely.
-
The contribution of linker histones to the stabilization of a fiber conformation due to cooperative or simultaneous binding to different DNA regions needs to be examined in further detail.
Given advancement in these three areas, reliable simulations and predictions of conformations adopted by the nucleosome/chromatosome chain appear to be feasible. This will make it possible to identify _targets for biological factors that affect the conformation of the chromatin fiber and with it the accessibility of the DNA sequence information.
SUPPLEMENTARY MATERIAL
To view all of the supplemental files associated with this article, visit www.biophysj.org.
Supplementary Material
Acknowledgments
We are grateful to Daniela Rhodes for valuable discussions and help, and to Felix Kepert, Reinhard Klement, M. R. S. Rao, Thomas Schalch, Tim Richmond, David Brown, Tom Misteli, and Vicki Roberts for providing Protein Data Bank coordinates of nucleosome, chromatosome, and fiber structures.
The project was supported by the Volkswagen Foundation in the program “New Conceptual Approaches to Modeling and Simulation of Complex Systems” and in the program “Junior Research Groups at German Universities”. Part of the computations were conducted within project mvb00007 of the North German Supercomputing Alliance (HLRN).
Editor: Klaus Schulten.
References
- 1.van Holde, K. E. 1989. Chromatin. Springer, Heidelberg.
- 2.Sproul, D., N. Gilbert, and W. A. Bickmore. 2005. The role of chromatin structure in regulating the expression of clustered genes. Natl. Rev. 6:775–781. [DOI] [PubMed] [Google Scholar]
- 3.Woodcock, C. L. 2006. Chromatin architecture. Curr. Opin. Struct. Biol. 16:213–220. [DOI] [PubMed] [Google Scholar]
- 4.Rippe, K., J. Mazurkiewicz, and N. Kepper. 2007. Interactions of histones with DNA: nucleosome assembly, stability and dynamics. In DNA interactions with Polymers and Surfactants. R. Dias and B. Lindman, editors. Wiley Blackwell, London.
- 5.Luger, K. 2006. Dynamic nucleosomes. Chromosome Res. 14:5–16. [DOI] [PubMed] [Google Scholar]
- 6.Widom, J. 1992. A relationship between the helical twist of DNA and the ordered positioning of nucleosomes in all eukaryotic cells. Proc. Natl. Acad. Sci. USA. 89:1095–1099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Travers, A. 1999. The location of the linker histone on the nucleosome. Trends Biochem. Sci. 24:4–7. [DOI] [PubMed] [Google Scholar]
- 8.Ramakrishnan, V. 1997. Histone H1 and chromatin higher-order structure. Crit. Rev. Eukaryot. Gene Expr. 7:215–230. [DOI] [PubMed] [Google Scholar]
- 9.Zlatanova, J., and K. van Holde. 1996. The linker histones and chromatin structure: new twists. Prog. Nucleic Acid Res. Mol. Biol. 52:217–259. [DOI] [PubMed] [Google Scholar]
- 10.Bednar, J., R. A. Horowitz, S. A. Grigoryev, L. M. Carruthers, J. C. Hansen, A. J. Koster, and C. L. Woodcock. 1998. Nucleosomes, linker DNA, and linker histone form a unique structural motif that directs the higher-order folding and compaction of chromatin. Proc. Natl. Acad. Sci. USA. 95:14173–14178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Leuba, S. H., C. Bustamante, J. Zlatanova, and K. van Holde. 1998. Contributions of linker histones and histone H3 to chromatin structure: scanning force microscopy studies on trypsinized fibers. Biophys. J. 74:2823–2829. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Zlatanova, J., S. H. Leuba, and K. van Holde. 1998. Chromatin fiber structure: morphology, molecular determinants, structural transitions. Biophys. J. 74:2554–2566. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Kepert, J. F., K. Fejes Tóth, M. Caudron, N. Mücke, J. Langowski, and K. Rippe. 2003. Conformation of reconstituted mononucleosomes and effect of linker histone H1 binding studied by scanning force microscopy. Biophys. J. 85:4012–4022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Howe, L., M. Iskandar, and J. Ausio. 1998. Folding of chromatin in the presence of heterogeneous histone H1 binding to nucleosomes. J. Biol. Chem. 273:11625–11629. [DOI] [PubMed] [Google Scholar]
- 15.Kepert, J. F., J. Mazurkiewicz, G. Heuvelman, K. Fejes Tóth, and K. Rippe. 2005. NAP1 modulates binding of linker histone H1 to chromatin and induces an extended chromatin fiber conformation. J. Biol. Chem. 280:34063–34072. [DOI] [PubMed] [Google Scholar]
- 16.Vignali, M., and J. L. Workman. 1998. Location and function of linker histones. Nat. Struct. Biol. 5:1025–1028. [DOI] [PubMed] [Google Scholar]
- 17.Brown, D. T., T. Izard, and T. Misteli. 2006. Mapping the interaction surface of linker histone H10 with the nucleosome of native chromatin in vivo. Nat. Struct. Mol. Biol. 13:250–255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Bharath, M. M., N. R. Chandra, and M. R. Rao. 2003. Molecular modeling of the chromatosome particle. Nucleic Acids Res. 31:4264–4274. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Fan, L., and V. A. Roberts. 2006. Complex of linker histone H5 with the nucleosome and its implications for chromatin packing. Proc. Natl. Acad. Sci. USA. 103:8384–8389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Hansen, J. C. 2002. Conformational dynamics of the chromatin fiber in solution: determinants, mechanisms, and functions. Annu. Rev. Biophys. Biomol. Struct. 31:361–392. [DOI] [PubMed] [Google Scholar]
- 21.Robinson, P. J., and D. Rhodes. 2006. Structure of the ‘30 nm’ chromatin fibre: a key role for the linker histone. Curr. Opin. Struct. Biol. 16:336–343. [DOI] [PubMed] [Google Scholar]
- 22.Stehr, R., N. Kepper, K. Rippe, and G. Wedeman. 2008. The effect of the nucleosome interaction potential on folding of the chromatin fiber. Biophys. J. 95:3677–3691. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Schalch, T., S. Duda, D. F. Sargent, and T. J. Richmond. 2005. X-ray structure of a tetranucleosome and its implications for the chromatin fibre. Nature. 436:138–141. [DOI] [PubMed] [Google Scholar]
- 24.Robinson, P. J., L. Fairall, V. A. Huynh, and D. Rhodes. 2006. EM measurements define the dimensions of the “30-nm” chromatin fiber: evidence for a compact, interdigitated structure. Proc. Natl. Acad. Sci. USA. 103:6506–6511. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Daban, J. R., and A. Bermudez. 1998. Interdigitated solenoid model for compact chromatin fibers. Biochemistry. 37:4299–4304. [DOI] [PubMed] [Google Scholar]
- 26.Katritch, V., C. Bustamante, and W. K. Olson. 2000. Pulling chromatin fibers: computer simulations of direct physical micromanipulations. J. Mol. Biol. 295:29–40. [DOI] [PubMed] [Google Scholar]
- 27.Wedemann, G., and J. Langowski. 2002. Computer simulation of the 30-nanometer chromatin fiber. Biophys. J. 82:2847–2859. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Sun, J., Q. Zhang, and T. Schlick. 2005. Electrostatic mechanism of nucleosomal array folding revealed by computer simulation. Proc. Natl. Acad. Sci. USA. 102:8180–8185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Mergell, B., R. Everaers, and H. Schiessel. 2004. Nucleosome interactions in chromatin: Fiber stiffening and hairpin formation. Phys. Rev. E. 70:011915. [DOI] [PubMed] [Google Scholar]
- 30.Aumann, F., F. Lankas, M. Caudron, and J. Langowski. 2006. Monte Carlo simulation of chromatin stretching. Phys. Rev. E. 73:041927. [DOI] [PubMed] [Google Scholar]
- 31.Pearlman, D. A., D. A. Case, J. W. Caldwell, W. R. Ross, T. E. Cheatham 3rd, S. DeBolt, D. Ferguson, G. Seibel, and P. Kollman. 1995. AMBER, a computer program for applying molecular mechanics, normal mode analysis, molecular dynamics and free energy calculations to elucidate the structures and energies of molecules. Comput. Phys. Commun. 91:1–41. [Google Scholar]
- 32.Cornell, W. D., P. Cieplak, C. I. Bayly, I. R. Gould, K. M. Merz, D. M. Ferguson, D. C. Spellmeyer, T. Fox, J. W. Caldwell, and P. A. Kollman. 1995. A second generation force field for the simulation of proteins, nucleic acids, and organic molecules. J. Am. Chem. Soc. 117:5179–5197. [Google Scholar]
- 33.Tsui, V., and D. A. Case. 2000. Theory and applications of the generalized Born solvation model in macromolecular simulations. Biopolymers. 56:275–291. [DOI] [PubMed] [Google Scholar]
- 34.Hawkins, G. D., C. J. Cramer, and D. G. Truhlar. 1996. Parameterized models of aqueous free energies of solvation based on pairwise descreening of solute atomic charges from a dielectric medium. J. Phys. Chem. 100:19824–19839. [Google Scholar]
- 35.Darden, T., D. York, and L. Pedersen. 1993. Particle mesh Ewald—An N.Log(N) method for Ewald sums in large systems. J. Chem. Phys. 98:10089–10092. [Google Scholar]
- 36.Humphrey, W., A. Dalke, and K. Schulten. 1996. VMD: Visual Molecular Dynamics. J. Mol. Graph. 14:33–38. [DOI] [PubMed] [Google Scholar]
- 37.Zewdie, H. 1998. Computer-simulation studies of diskotic liquid crystals. Phys. Rev. E. 57:1793–1805. [Google Scholar]
- 38.Garcia de la Torre, J., S. Navarro, M. C. Lopez Martinez, F. G. Diaz, and J. J. Lopez Cascales. 1994. HYDRO: a computer program for the prediction of hydrodynamic properties of macromolecules. Biophys. J. 67:530–531. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Rippe, K. 2001. Making contacts on a nucleic acid polymer. Trends Biochem. Sci. 26:733–740. [DOI] [PubMed] [Google Scholar]
- 40.Woodcock, C. L., S. A. Grigoryev, R. A. Horowitz, and N. Whitaker. 1993. A chromatin folding model that incorporates linker variability generates fibers resembling the native structures. Proc. Natl. Acad. Sci. USA. 90:9021–9025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Schiessel, H., W. M. Gelbart, and R. Bruinsma. 2001. DNA folding: structural and mechanical properties of the two- angle model for chromatin. Biophys. J. 80:1940–1956. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Cui, Y., and C. Bustamante. 2000. Pulling a single chromatin fiber reveals the forces that maintain its higher-order structure. Proc. Natl. Acad. Sci. USA. 97:127–132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Ramakrishnan, V., J. T. Finch, V. Graziano, P. L. Lee, and R. M. Sweet. 1993. Crystal structure of globular domain of histone H5 and its implications for nucleosome binding. Nature. 362:219–223. [DOI] [PubMed] [Google Scholar]
- 44.Clark, K. L., E. D. Halay, E. Lai, and S. K. Burley. 1993. Co-crystal structure of the HNF-3/fork head DNA-recognition motif resembles histone H5. Nature. 364:412–420. [DOI] [PubMed] [Google Scholar]
- 45.Bharath, M. M., N. R. Chandra, and M. R. Rao. 2002. Prediction of an HMG-box fold in the C-terminal domain of histone H1: insights into its role in DNA condensation. Proteins. 49:71–81. [DOI] [PubMed] [Google Scholar]
- 46.Mamoon, N. M., Y. Song, and S. E. Wellman. 2002. Histone h1(0) and its carboxyl-terminal domain bind in the major groove of DNA. Biochemistry. 41:9222–9228. [DOI] [PubMed] [Google Scholar]
- 47.Catez, F., T. Ueda, and M. Bustin. 2006. Determinants of histone H1 mobility and chromatin binding in living cells. Nat. Struct. Mol. Biol. 13:305–310. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Arya, G., and T. Schlick. 2006. Role of histone tails in chromatin folding revealed by a mesoscopic oligonucleosome model. Proc. Natl. Acad. Sci. USA. 103:16236–16241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Butler, P. J., and J. O. Thomas. 1980. Changes in chromatin folding in solution. J. Mol. Biol. 140:505–529. [DOI] [PubMed] [Google Scholar]
- 50.Pearson, E. C., P. J. Butler, and J. O. Thomas. 1983. Higher-order structure of nucleosome oligomers from short-repeat chromatin. EMBO J. 2:1367–1372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Ausio, J., N. Borochov, D. Seger, and H. Eisenberg. 1984. Interaction of chromatin with NaCl and MgCl2. Solubility and binding studies, transition to and characterization of the higher-order structure. J. Mol. Biol. 177:373–398. [DOI] [PubMed] [Google Scholar]
- 52.Gale, J. M., and M. J. Smerdon. 1988. UV-induced pyrimidine dimers and trimethylpsoralen cross-links do not alter chromatin folding in vitro. Biochemistry. 27:7197–7205. [DOI] [PubMed] [Google Scholar]
- 53.Crothers, D. M., and B. H. Zimm. 1965. Viscosity and sedimentation of the DNA from bacteriophages T2 and T7 and the relation to molecular weight. J. Mol. Biol. 12:525–536. [DOI] [PubMed] [Google Scholar]
- 54.Gray, H. B., Jr., V. A. Bloomfield, and J. E. Hearst. 1967. Sedimentation coefficients of linear and cyclic worm like coils with excluded-volume effects. J. Chem. Phys. 46:1493–1498. [Google Scholar]
- 55.Pearson, E. C., D. L. Bates, T. D. Prospero, and J. O. Thomas. 1984. Neuronal nuclei and glial nuclei from mammalian cerebral cortex. Nucleosome repeat lengths, DNA contents and H1 contents. Eur. J. Biochem. 144:353–360. [DOI] [PubMed] [Google Scholar]
- 56.Fan, Y., T. Nikitina, J. Zhao, T. J. Fleury, R. Bhattacharyya, E. E. Bouhassira, A. Stein, C. L. Woodcock, and A. I. Skoultchi. 2005. Histone H1 depletion in mammals alters global chromatin structure but causes specific changes in gene regulation. Cell. 123:1199–1212. [DOI] [PubMed] [Google Scholar]
- 57.Woodcock, C. L., A. I. Skoultchi, and Y. Fan. 2006. Role of linker histone in chromatin structure and function: H1 stoichiometry and nucleosome repeat length. Chromosome Res. 14:17–25. [DOI] [PubMed] [Google Scholar]
- 58.Mazurkiewicz, J., J. F. Kepert, and K. Rippe. 2006. On the mechanism of nucleosome assembly by histone chaperone NAP1. J. Biol. Chem. 281:16462–16472. [DOI] [PubMed] [Google Scholar]
- 59.Catez, F., D. T. Brown, T. Misteli, and M. Bustin. 2002. Competition between histone H1 and HMGN proteins for chromatin binding sites. EMBO Rep. 3:760–766. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.van Holde, K., and J. Zlatanova. 1996. What determines the folding of the chromatin fiber. Proc. Natl. Acad. Sci. USA. 93:10548–10555. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Gerchman, S. E., and V. Ramakrishnan. 1987. Chromatin higher-order structure studied by neutron scattering and scanning transmission electron microscopy. Proc. Natl. Acad. Sci. USA. 84:7802–7806. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Dimitrov, S. I., V. L. Makarov, and I. G. Pashev. 1990. The chromatin fiber: structure and conformational transitions as revealed by optical anisotropy studies. J. Biomol. Struct. Dyn. 8:23–35. [DOI] [PubMed] [Google Scholar]
- 63.Kubista, M., P. Hagmar, P. E. Nielsen, and B. Norden. 1990. Reinterpretation of linear dichroism of chromatin supports a perpendicular linker orientation in the folded state. J. Biomol. Struct. Dyn. 8:37–54. [DOI] [PubMed] [Google Scholar]
- 64.Draves, P. H., P. T. Lowary, and J. Widom. 1992. Co-operative binding of the globular domain of histone H5 to DNA. J. Mol. Biol. 225:1105–1121. [DOI] [PubMed] [Google Scholar]
- 65.Thomas, J. O., C. Rees, and J. T. Finch. 1992. Cooperative binding of the globular domains of histones H1 and H5 to DNA. Nucleic Acids Res. 20:187–194. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Dekker, J., K. Rippe, M. Dekker, and N. Kleckner. 2002. Capturing chromosome conformation. Science. 295:1306–1311. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.