Abstract
Lysosomes are acidic organelles and are involved in various diseases, the most prominent is malaria. Accumulation of molecules in the cell by diffusion from the external solution into cytosol, lysosome and mitochondrium was calculated with the Fick-Nernst-Planck-equation. The cell model considers the diffusion of neutral and ionic molecules across biomembranes, dissociation to mono- or bivalent ions, adsorption to lipids, and electrical attraction or repulsion. Based on simulation results, high and selective accumulation in lysosomes was found for weak mono- and bivalent bases with intermediate to high log Kow. These findings were validated with experimental results and by a comparison to the properties of antimalarial drugs in clinical use. For ten active compounds, nine were predicted to accumulate to a greater extent in lysosomes than in other organelles, six of these were in the optimum range predicted by the model and three were close. Five of the antimalarial drugs were lipophilic weak dibasic compounds. The predicted optimum properties for a selective accumulation of weak bivalent bases in lysosomes are consistent with experimental values and are more accurate than any prior calculation. This demonstrates that the cell model can be a useful tool for the design of effective lysosome-_targeting drugs with minimal off-_target interactions.
Keywords: accumulation, base, drug design, lysosome, malaria, model
INTRODUCTION
Recently we described the accumulation of molecules in mitochondria of human cells (both normal and tumor cells) with a biophysical model of a single cell (Trapp and Horobin 2005). This first cell model considered only the cytosol, that is the cell sap and lipids, and mitochondria (highly charged alkaline organelles). Now we extend this cell model to lysosomes, acidic organelles present in most animal cells. Models describing the movement of molecules within cells are not only useful for the interpretation of experiments, but may also help in designing more effective drugs (Chen and Rosania 2006).
Acidic intracellular organelles – such as late endosomes, phagosomes and lysosomes – are widely implicated in the pathogenesis of many parasitic, microbial and viral diseases. Many drugs in clinical use accumulate in lysosomes, this accumulation sometimes being an essential component of the drug’s mechanism of action. The antimalarial drug chloroquine, for example, forms toxic complexes with byproducts of hemoglobin metabolism that accumulate in the lysosomes of the malaria parasite inside erythrocytes (Slater 1993, Zhang et al. 1999, Ginsburg et al. 1999, Sugioka et al. 1987). In a different example, lysosomal accumulation of several antipsychotic and antidepressant drugs, a consequence of their physiochemical characteristics (Kaufmann and Krise 2007, Kornhuber et al. 2008), can contribute to clinical antidepressive effects via inhibition of the intralysosomal acid sphingomyelinase (Kornhuber et al. 2005, 2008). But also if the site of action of a drug is not lysosomal, side-effects associated with unintentional lysosomal accumulation may occur. Recently, sequestration of anticancer drugs in acidic intracellular organelles has been studied as a mechanism determining the cell type-selectivity of candidate anticancer agents (Duvvuri et al. 2004, Duvvuri and Krise 2005). Lysosomal drug sequestration can also underlie rapid clearance of anticancer drugs from intrinsically drug resistant cancer cells (Chen and Rosania 2006).
The first comprehensive discussion of factors leading to accumulation of drugs inside lysosomes dates back over thirty years (De Duve et al. 1974), when it was first appreciated that lysosomes are acidic organelles with respect to the cytosol. This results in “ion trapping” of weak bases, as neutral molecules diffuse into the lysosome where, after protonation, they form more hydrophilic species slow to diffuse out (De Duve et al. 1974, MacIntyre and Cutler 1988). An analogous ion trap effect underlies weak acids’ accumulation in mitochondria (Rashid and Horobin 1991) and accumulation of weak acids in plant cells (Raven 1975). Raven described the transport of the anion in the cell with the Nernst-Planck equation, which considers the effect of electrical fields. A combination of Fick's diffusion law and Nernst-Planck equation was used to predict the intracellular location of drugs in human cells (Trapp and Horobin 2005, Zhang et al. 2006). This model is extended to molecules with either one or two acidic or basic functional groups, including ampholytes and zwitterions. The new set of equations developed in the present paper predicts the localization of molecules in solution and lipids of mitochondria, cytosol and lysosomes. Physicochemical property combinations leading to selective accumulation of molecules in lysosomes are identified and compared to earlier findings and the properties of anti-malarial drugs in clinical use.
METHODS
Cell model simulating uptake and accumulation of molecules in cells
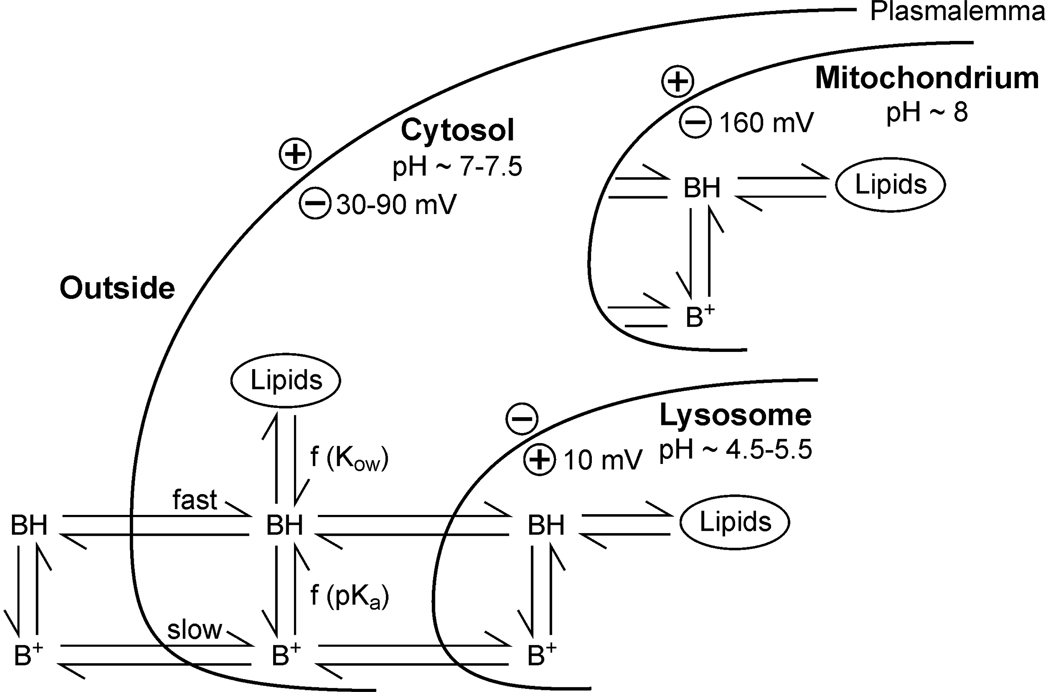
The model’s objective is to predict diffusive movement and distribution of molecules in a living cell. Figure 1 shows the processes involved in the uptake of a weak base (BH). The cell is separated into cytosol, lysosome and mitochondrium. Each compartment consists of an aqueous and a lipid fraction and is surrounded by a biomembrane.
Figure 1.
Structure of the cell system considered in the model approach.
Flux of neutral molecules across membranes
The diffusive flux of neutral molecules across membranes, Jn, is driven by the chemical potential, and is described by Fick’s 1st Law of Diffusion:
| (1) |
where J is the unit net flux of the neutral molecules n from outside (o) to inside (i) of the membrane (kg m−2 s−1), Pn is the permeability of the membrane (m s−1) for neutral molecules, and a is the activity of the compound (kg m−3).
Flux of electrolytes across membranes
The unit net flux of the dissociated (ionic) molecule species across electrically charged membranes, Jd, is described by an analytical solution of the the Nernst-Planck equation (Briggs et al. 1961):
| (2) |
where Pd is the permeability of the membrane (m s−1) for dissociated molecules, N = z E F / (R T); z is the electric charge (synonym valency, for acids −, for bases +), F is the Faraday constant (96 484.56 C mol−1), E is the membrane potential (V), R is the universal gas constant (8.314 J mol−1 K−1) and T is the absolute temperature (K).
The total net flux J is the sum of Jn and Jd
| (3) |
Active transport across membranes (e.g. by transporter proteins or pinocytotic endocytosis) is not considered in this model, but may be added, if required, by an additional flux term.
Molecule fractions
Under physiologically relevant conditions, molecules of organic electrolytes may exist as ions or in a neutral form. The activity ratio D between both is calculated by the Henderson-Hasselbalch equation (Henderson 1908):
| (4) |
where a is the activity, d is the index for dissociation (synonym ionized), n for neutral, i is 1 for bases and −1 for acids; pKa is the negative logarithm (log10) of the dissociation constant.
While in most cases the total concentration of a compound is measured by chemical analysis, the activity is the driving force for exchange (see eq. 1 to eq. 3). The total (measurable) concentration Ct of the compound is comprised of neutral (n) and dissociated (d) molecules, both can be in solution or adsorbed. Only the free, non-adsorbed molecules, neutral (index n) or dissociated (index d), participate in diffusive exchange processes. The relation between total concentration Ct (kg m3) and the activity a (kg m3) of free (truly dissolved) molecules is
| (5) |
The respective fraction freely dissolved neutral molecules, fn, is calculated by
| (6) |
where W is the volumetric water fraction, γ is the activity coefficient, with a = γ C. Kn and Kd are the sorption coefficients of the neutral and the dissociated molecule. Per definition ad = an × D, and the fraction of freely dissolved dissociated molecules, fd, is fd = ad|Ct = D × fn.
Bivalent Ions
A bivalent electrolyte, acid or base, has two dissociation processes (shown for the base):
with two corresponding pKa–values, pKa1 and pKa2, giving the activity ratios
| (8a) |
| (8b) |
It follows for the activity of the neutral molecule, the first ion B+, and the second ion B++ that an + ad1 + ad2 = 1 and
| (9a) |
| (9b) |
| (9c) |
Furthermore, we define the ratios D1 = ad1/an and D2 = ad2/an in order to calculate the respective fractions for the activities, fn, fd1 and fd2
| (10) |
The total net flux of all molecule species J is the sum of the net flux of the neutral molecule, the monovalent ion, and the bivalent ion
| (11) |
where N1 = z1 E F / (R T) and N2 = z2 E F / (R T), with z1 is the electric charge of the first dissociated ion (+1 for bases), and z2 is the charge of the second dissociated ion (+2 for bases). The same formalism is applied to bivalent acids, ampholytes and zwitterions.
Multi-organelle model
The multi-organelle model consists of cytosol, lysosomes and mitochondria. Since lysosomes and mitochondria are totally enclosed by cytosol, calculation of the uptake of molecules into these organelles first requires solution of the equations for uptake from outside into the cytosol, and then for uptake from cytosol into mitochondria and lysosomes.
If o denotes the outside of the cell, c the cytosol, m the mitochondria, l the lysosome, and J the corresponding unit fluxes across surface area A, then the
| cytosol (14a) |
change of mass in the lysosome ml = + flux to lysosome – flux to cytosol
| lysosome (14b) |
change of mass in the mitochondrium mm = + flux to mitochondrium – flux to cytosol
| mitochondrium (14c) |
Concentrations C are derived by the relation C = m/V, where V is the volume.
Solution method
The equations for the n × n = 3 matrix (cytosol, lysosomes, mitochondria) were solved numerically (Euler method) and compared to an analytical solution with two parallel n × n = 2 matrices (cytosol and lysosomes; cytosol and mitochondria). Differences were very small, except in the very early stage of the simulations. All subsequent calculations used two parallel 2 × 2 matrices solved analytically.
Model parameterization
Generic data for cytosol, lysosomes and mitochondria, listed in Table 1, were taken from several sources and do not represent a special scenario. Volume, surface area, water and lipid content, ionic strength, pH and electrical potential at the biomembrane describe each compartment. The cytosol is neutral (default value 7.0), the lysosomal pH is acidic (default value pH 5) and the pH in mitochondria is alkaline (8.0). The external pH is 7.4, which is the normal pH of blood and also the pH of many nutrition media used in experimental work. The electrical potential at the plasmalemma (plasma membrane) is −70 mV, at the lysosomal membrane is slightly positive (+10 mV), and at the mitochondrium −160 mV. All generic values can be changed and adapted to actual cell conditions. The model is based on a “constant field approach” (Goldman 1943, Hodgkin and Katz 1949), therefore pH and electrical potential of the compartments do not change due to uptake of electrolytes. Chemical data required as input are dissociation constant(s) pKa; electric charge(s) z; activity coefficients γ; membrane permeabilities P; and sorption coefficients K of both the neutral and the dissociated compound(s). The parameters P and K can be estimated from log KOW.
Table 1.
Parameters of a generic human cell.
| Parameter | Symbol | Value | Unit | Reference |
|---|---|---|---|---|
| Diameter cell a | 10−5 | m | generic | |
| Diameter lysosome | 1.71 × 10−6 | b | ||
| Diameter mitochondrium | 10−6 | m | generic | |
| pH outside | pHo | 7.4 | - | Rodgers et al. (2005) |
| pH cytosol | pHc | 7.0 | - | Rodgers et al. (2005) |
| pH lysosome | pHl | 5 | - | Ohkuma and Pool (1978) |
| pH mitochondrium | pHm | 8 | - | generic |
| Water content | W | 0.95 | L/L | all organelles |
| Lipid content | L | 0.05 | g/g | all organelles |
| Ionic strength outside | Io | 0 | mol | |
| Ionic strength in cell | I | 0.3 | mol | all organelles |
| Plasmalemma membrane potential | Ec | −0.07 | V | generic |
| Lysosomal membrane potential | Em | +0.01 | V | Van Dyke (1988) |
| Mitochondrial membrane potential | Em | −0.16 | V | Trapp and Horobin (2005) |
Volume and surface area were calculated from diameter assuming a sphere
Value chosen to get a volume ratio lysosome to cytosol of 1 : 200 (De Duve et al. 1974).
The permeability of neutral molecules is calculated from membrane thickness, partitioning into the membrane and diffusion coefficient of organic molecules in the membrane, which leads to the equation (Trapp and Horobin 2005) log P = log KOW − 6.7 for the neutral molecule and log P = log KOW − 10.2 for the ion. Thus, the default permeability ratio between neutral and ionic species is 3162:1. The sorption parameter K is calculated from K = L × KOW, where L is the lipid content (L L−1). For the ion, log KOW is taken 3.5 log-units lower than for the neutral molecule.
The activity coefficients γn of neutral molecules, z = 0, were calculated from the ionic strength I (mol) with the Setchenov equation to 1.23 at I = 0.3 mol. The activity coefficients of ions, γd, were calculated with the Davies approximation of the modified Debye-Hückel equation (Appelo and Postma 1999) and are 0.74 for monovalent ions, |z| = 1, and 0.3 for bivalent ions, |z| = 2, at I = 0.3 mol.
RESULTS
The physico-chemical input parameters were varied systematically to determine chemical properties that lead to accumulation of xenobiotics in lysosomes or other parts of the cell.
Monovalent bases (z = +1)
The first group of compounds investigated are weak bases. It has long been known that such compounds accumulate in lysosomes due to the ion trap mechanism (De Duve 1974).
Impact of pKa on accumulation of bases in lysosomes
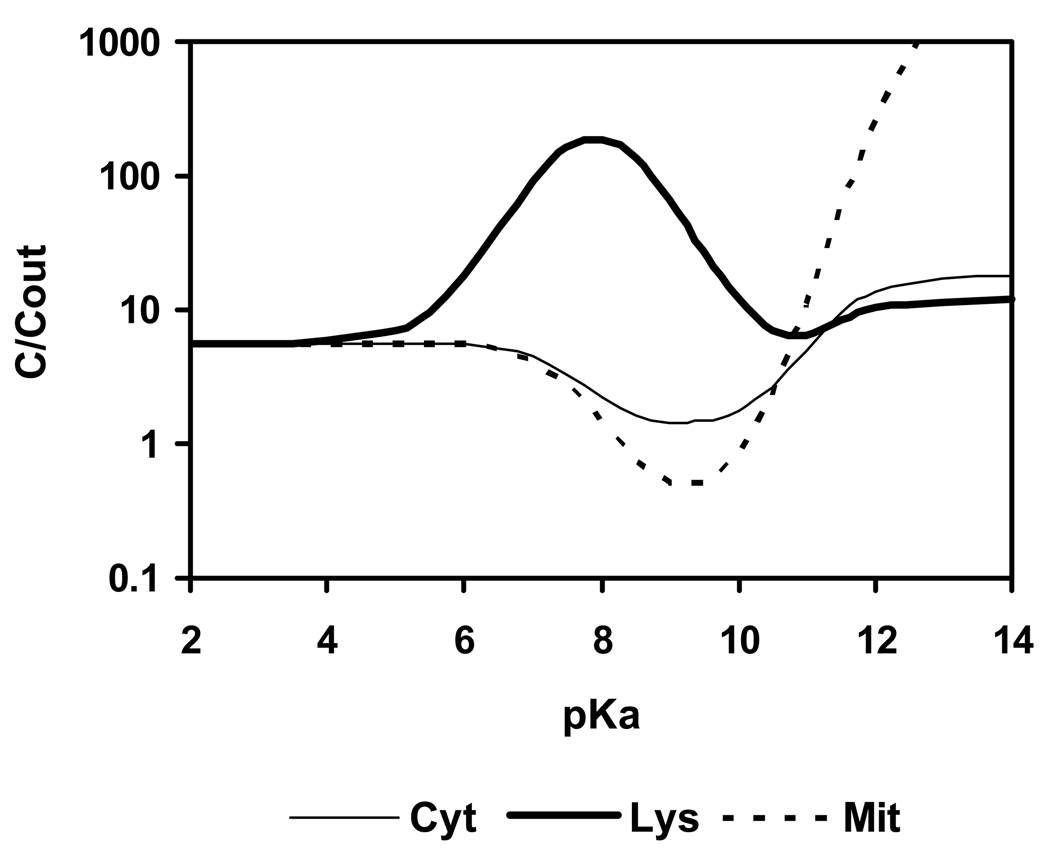
Figure 2 shows the calculated uptake from outside into cytosol, lysosomes and mitochondria of a monovalent weak base with a constant log KOW of 2 and varying pKa. The calculations were made for 1 h exposure to the external medium. In agreement with De Duve et al.’s commentary (1974) the model predicts accumulation in lysosomes to be greater than in cytosol and mitochondria for bases with pKa between 6 and 10, with the optimum located near 8. The mechanism of this accumulation is the ion trap, involving uptake of the neutral base into acidic lysosomes with trapping following protonation. At the same pKa, weak bases are excluded, by an opposite ion trap mechanism, from cytosol and mitochondria, while at high pKa (> 12) an attraction of cations by the strong negative electrical field of the mitochondria is predicted. The exact maximum concentration ratio lysosome to outside occurs at pKa = 7.9, and is 191:1 for an intralysosomal pH of 5, with > 99% of the molecules in lysosomes being in solution.
Figure 2.
Calculated uptake of a monovalent weak base with log KOW = 2 and varying pKa from outside into cytosol (Cyt), lysosomes (Lys) and mitochondria (Mit); t = 1 h, log scale.
Log KOW
With the default parameterization, the uptake into lysosomes is slow for polar weak bases (log KOW < 0). For highly lipophilic bases (log KOW > 3), sorption to cytosolic lipids becomes the dominant process. Thus, the optimum for selective accumulation in lysosomes is at 0 < log KOW < 3 (not shown).
Impact of membrane permeability of ions on accumulation of bases in lysosomes
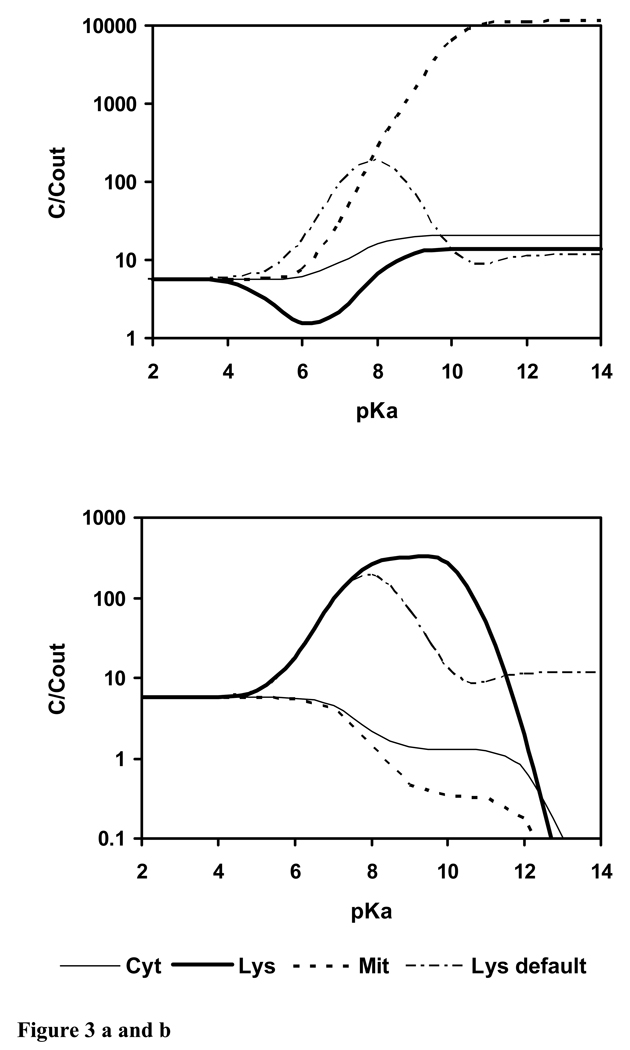
Membrane permeability of the ion is a critical parameter. It was shown that the ratio of membrane permeabilities in the dissociated and neutral state strongly influences lysosomal accumulation (Duvvuri et al. 2004). We therefore generated a simulation analogous to Figure 2 but assuming equal permeability of ion and neutral molecule (Fig. 3a). Dramatically, the model no longer predicts accumulation of weak bases in lysosomes but instead predicts accumulation by mitochondria if pKa ≥ 6. This is in accordance with experimental findings for rhodamine 123 and rhodamine 6G (Duvvuri et al. 2004).
Figure 3.
Calculated uptake of a monovalent weak base with log KOW = 2 and varying pKa from outside into cytosol, lysosomes and mitochondria; t = 1 h. a) Pd : Pn = α = 1; b) Pd : Pn = α = 0; “Lys default” is the simulation with the default ion membrane permeability of the model (Fig. 2), corresponding to α = 1 : 3162.
The issue of whether ions can cross membranes, and if so how fast, has been recently discussed (Saparov et al. 2006). If it is assumed that ions cannot cross biomembranes, then the permeability of the ion is zero. The effect on intracellular localization is shown in Figure 3b. The ion trap increases, the concentration ratio lysosomes to outside is higher, and the optimum pKa region is shifted towards pKa 10, compared to the original simulation in Fig. 2 (“Lys default” in Fig. 3), which was done with the default ion membrane permeability. Compounds with pKa > 12, which are practically completely dissociated outside at pH 7.4, are not taken up at all if ions cannot cross biomembranes (Fig. 3b).
Bivalent bases (z = +2)
Optimum pKa-values
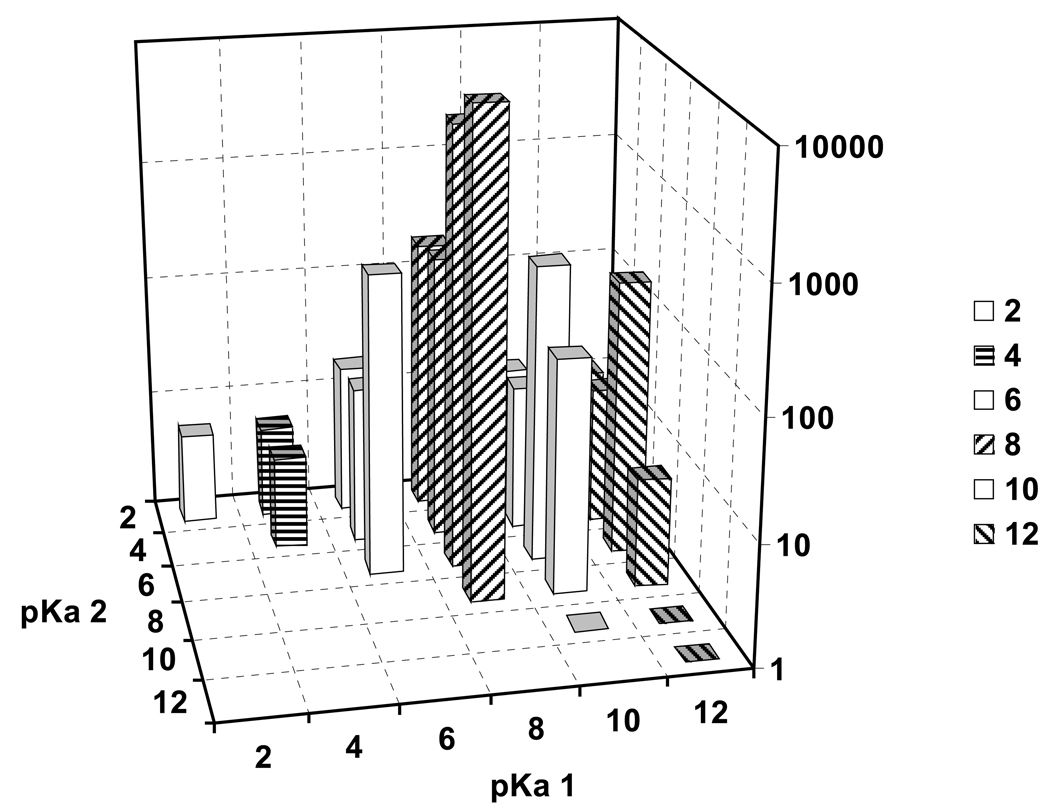
The concentration ratio lysosome to outside of a lipophilic bivalent base (log KOW = 2) after 1 h exposure and for varying pKa1 and pKa2 is shown in Figure 4. With two dissociating basic groups, the concentration ratio can be much higher than with one. The maximum concentration ratio lysosome to outside is found when pKa1 is near 8 and and pKa2 is 8 or somewhat lower, between 6 and 8, and is > 10 000. Optimum accumulation equals the maximum for a monovalent base to the power 2 multiplied with factor 2 for the lower activity coefficient of bivalent ions.
Figure 4.
Calculated uptake (t = 1 h) of a bivalent weak base with log KOW = 2 and varying pKa1 and pKa2 from outside into lysosomes; t = 1 h.
Uptake of bivalent bases into cytosol is lower and more evenly distributed, with maximum values of C/Cout of 18 at pKa1 = 12 and pKa2 = 6 (not shown). Uptake into mitochondria is highest for pKa1 above 12 and has a minimum in the region of pKa1 near 8 (not shown). Thus, weak bivalent bases with both pKa values near 8 are predicted to have almost exclusive lysosomal accumulation.
Impact of lipophilicity (log KOW) on lysosomal accumulation of bivalent bases
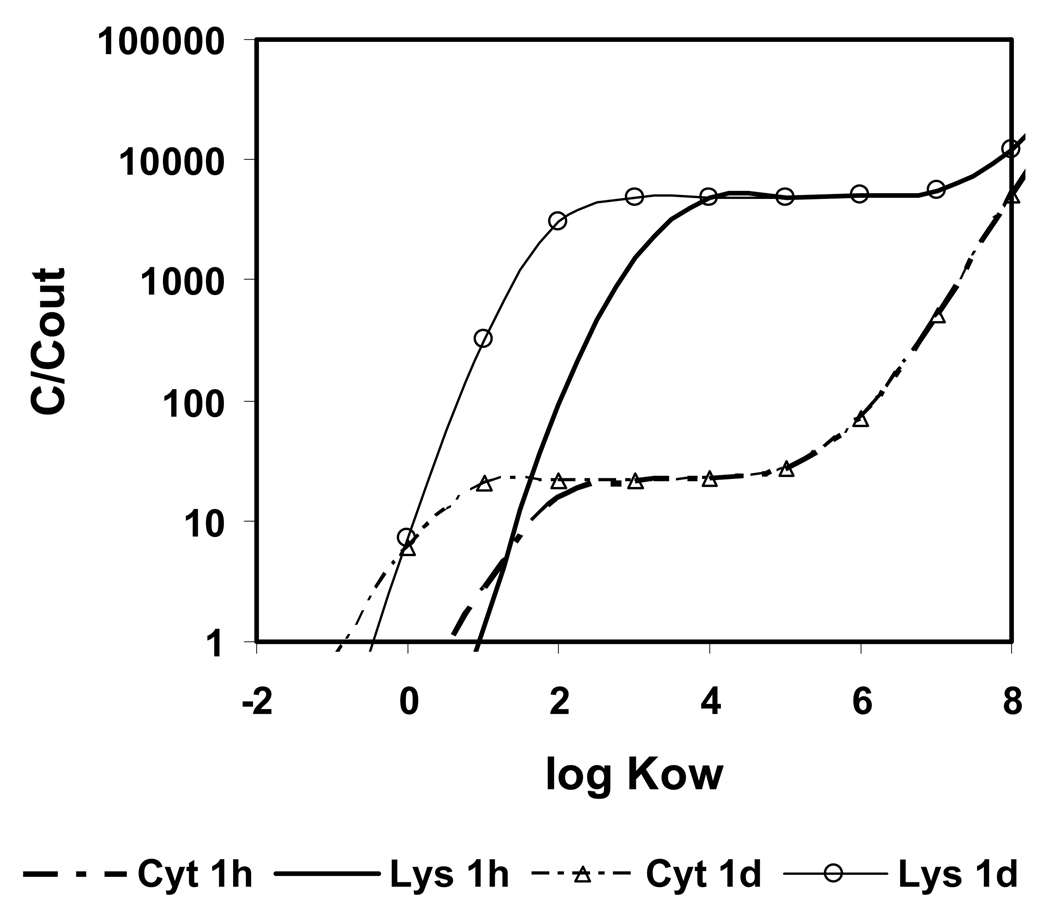
Fully dissociated bivalent bases are much more hydrophilic than the corresponding neutral molecules. Predicted uptake of hydrophilic compounds into cells is slow, and only lipophilic bivalent bases are taken up within therapeutically reasonable time periods (within days) into cells. The impact of log KOW on the uptake of a bivalent base with pKa1 = 10 and pKa2 = 8 (properties similar to chloroquine) from outside the cell into lysosomes and cytosol for varying log KOW and t = 1 h and 1d is shown in Figure 5. For log KOW < 3, uptake is kinetically limited. With increasing log KOW, the bivalent weak base shows increasing accumulation in lysosomes, until a plateau is reached with log KOW > 4. If the compound is very lipophilic (log KOW > 6), accumulation increases in cytosol, due to sorption to intracellular lipids, and the exclusivity of accumulation in lysosomes is lost. Thus, the optimum for selective accumulation of bivalent bases in lysosomes is at 3 < log KOW < 6, which is higher than for the monovalent bases.
Figure 5.
Calculated concentration ratio cytosol (Cyt), lysosomes (Lys) and mitochondria (Mit) to outside for a bivalent base with pKa1 = 10, pKa2 = 8 and varying log KOW.
Significantly, the anti-malaria agent and lysosome-_targeting drug par excellence (De Duve 1974) chloroquine is a bivalent base with pKa1 at 9.94, pKa2 at 8.10 (Newton and Kluza 1978). The log KOW of chloroquine is 4.38 (Hansch et al. 1995). Accumulation of chloroquine in lysosomes “several hundred-fold” has been observed (De Duve et al. 1974). Quinacrine, another bivalent base accumulating in lysosomes (Duvvuri et al. 2004) has a log KOW of 4.79 and pKa-values at 10.2 and 8.2 (Hansch et al. 1995, Newton and Kluza 1978). The properties of both compounds are in the predicted optimum range.
Impact of lysosomal pH on accumulation of bases
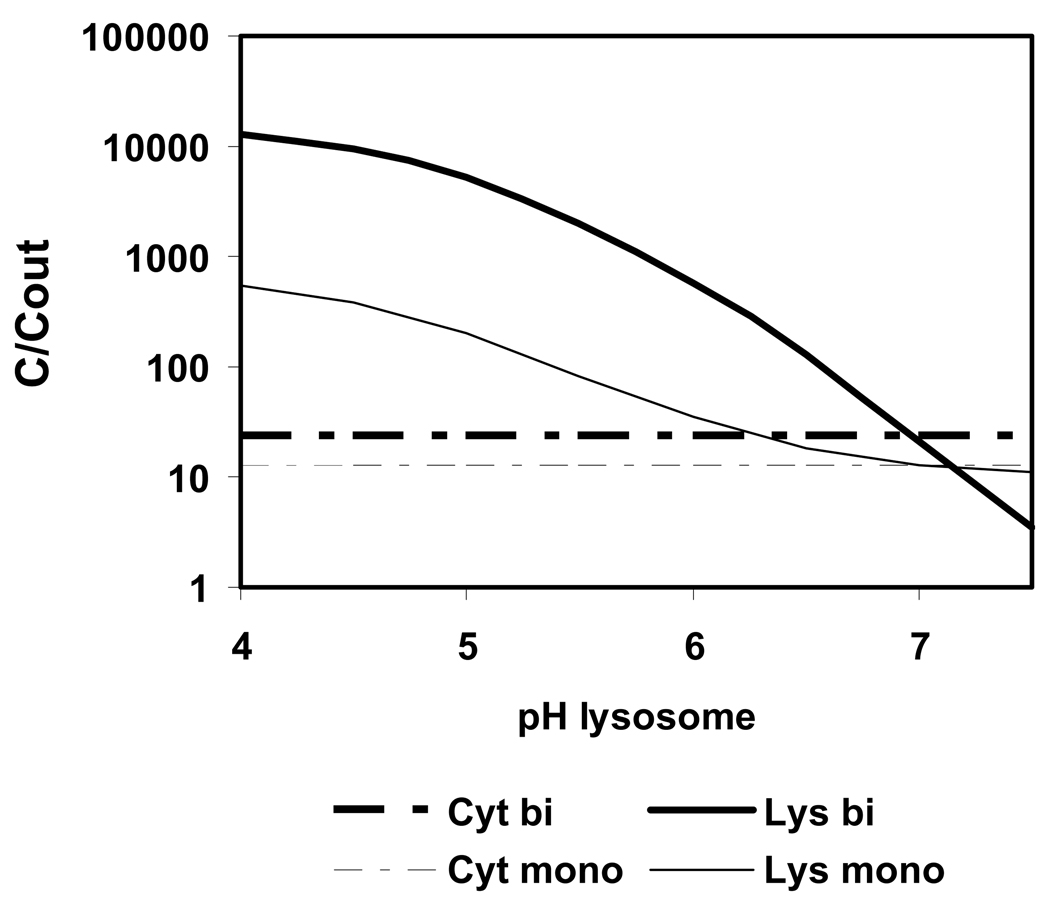
A rise of the intralysosomal pH from 5.6 to above 7 due to uptake of basic compounds into this organelle has been observed (Ishizaki et al. 2000). However, a pH-gradient between external solution and lysosomes is essential for the ion trap effect. If the pH of lysosomes increases, then the accumulation of basic compounds decreases. Figure 6 shows the predicted accumulation of a bivalent base with properties of chloroquine, and of a monovalent base with log KOW at 3 and pKa at 8. The external pH is 7.4. The highest accumulation is calculated for the lowest pH in lysosomes, i.e. pH 4. With increasing lysosome pH, the accumulation decreases. When the pH in lysosomes has reached the pH in cytosol (pH is 7), no ion trap and no accumulation occurs.
Figure 6.
Calculated uptake of a bivalent base (bi) with the properties of chloroquine (log KOW is 4.38; pKa1 is 9.94; pKa2 is 8.10) and of a monovalent base (mono) (log KOW is 3, pKa is 8) from outside into cytosol (Cyt) and lysosomes (Lys) for varying pH in lysosomes; t = 1 h.
It seems thus unlikely that the predicted maximum lysosomal accumulation, which is above factor 10 000, is reached in reality. Even at very low external concentrations, such as 1 µM, concentrations inside lysosomes would be 10 mM, and this rises the intralysosomal pH. This is a negative feedback mechanism which reduces lysosomal accumulation of bases, as was confirmed experimentally by Ishizaki et al. (2000).
Monovalent acids (z = −1)
It has been stated that “weak acids are kept out of lysosomes” (De Duve 1974). For most acids, our model confirms this: hydrophilic and less lipophilic acids (log KOW ≤ 5) do not reach higher levels in lysosomes than in cytosol or mitochondria for any pKa value between 0 and 14. Uptake of strong acids is kinetically limited. Only lipophilic acids (log KOW ≥ 6 of the neutral molecule) show uptake into the cell, and the positive electrical potential at the lysosomal membrane (+10 mV) leads to attraction of the electrically negatively charged acid ion. The effect is small, however, the concentration of anions in lysosomes is maximally 46% above that in cytosol (not shown).
Bivalent acids (z = −2)
The same phenomenon, electrical attraction of the ion, is even more pronounced (up to factor 2.2 higher accumulation in lysosome than in any other organelle) with strong bivalent acids (pKa1 and pKa2 ≤ 1.5). However, since bivalent ions are more hydrophilic, it requires a very high log KOW (≥ 9 for the neutral molecule), otherwise uptake into the cell is kinetically limited. At these high log KOW values, trapping in membranes is likely (Horobin et al. 2006). A second region of selective lysosomal accumulation occurs with bivalent lipophilic acids with one strong and one weak (pKa ≥ 7) acidic group, where the bivalent acid dissociates only once under the conditions in the cell, and behaves identically to a monovalent acid.
Ampholytes
Many drugs contain a combination of basic and acidic functional groups and are classified as ampholytes (+R / R / R−) or zwitterions (+R / +R− / R−). Such molecules may accumulate in lysosomes. For example, accumulation of propranolol has been observed (Ishizaki et al. 2000, Lemieux et al. 2004). Propranolol has a basic group with pKa 9.14 and an acidic OH group with pKa at 13.84 (ACD 2007). The model predicts that ampholytes (+R / R / R−) with the basic group with pKa near 8 (weak base) and weak acid group (pKa ≥ 6) accumulate in lysosomes. With this combination of properties, the acidic group is of minor importance, the ampholyte is ion-trapped in lysosomes like a weak base. In general, the model predicts that a strongly acidic group together with a weakly basic group leads to much reduced lysosomal accumulation compared to a corresponding monovalent base lacking this acidic group.
Zwitterions
Zwitterions (+R−), possessing two charges of equal magnitude but opposite charge sign, have a low lipophilicity (log KOW), similar to mono-charged acid or base species (Hansch et al. 1995). Membrane permeabilities of the three possible molecule species (+R / +R− / R−) do not differ much, therefore, the ion trap in lysosomes does not build up. Therefore, zwitterions are principally not suited well to _target lysosomes.
DISCUSSION
Comparison to experimental findings
Two different types of data can be used for a validation of the model predictions. The first data is experimental studies to lysosomal accumulation, the second is the investigation of drugs known to _target lysosomal diseases.
Quantitative measurements of concentration in lysosomes
Due to the intrinsic difficulties to measure chemical concentrations in the small organelles lysosomes, only a few studies with quantitative concentration data are available.
Duvvuri and Krise (2005b) quantitatively assessed the accumulation of two bases in lysosomes. The compounds studied were Lysotracker red DND-99 (LTR) and quinacrine (QNC). LTR is a monovalent base with log KOW at 2.1 and pKa of 7.5 (Duvvuri et al. 2004). QNC is a bivalent base with log KOW at 4.69 and pKa-values at 10.47 and 7.12 (ACD 2007), 10.2 and 8.2 (Newton and Kluza 1978) or 10.39 und 7.72 (Rosenberg and Schulman 1978). Both LTR and QNC accumulate in lysosomes. The measured concentration ratio between lysosome and external medium was 60 for LTR and 760 for quinacrine (Duvvuri and Krise, 2005b). The model prediction is 58 for LTR and 487 to 1500 for QNC, depending on the pKa-data used and the lysosomal pH.
Duvvuri et al. (2005) measured also the lysosomal accumulation of a series of structurally identical monovalent weak bases with similar lipophilicity (log KOW between 1.26 and 1.65), but varying pKa (from 4.0 to 9.0). The measured concentration ratio between lysosomes and cytosol varied over factor 20, with lowest values (4.0 and 3.0) for the compounds with low pKa-values (4 and 5) and highest values at pKa 7.4 and 9 (53 and 57). The model, too, predicts an increase of the concentration ratio with increasing pKa, from 1.0 at pKa 4 to 50 at pKa 9.
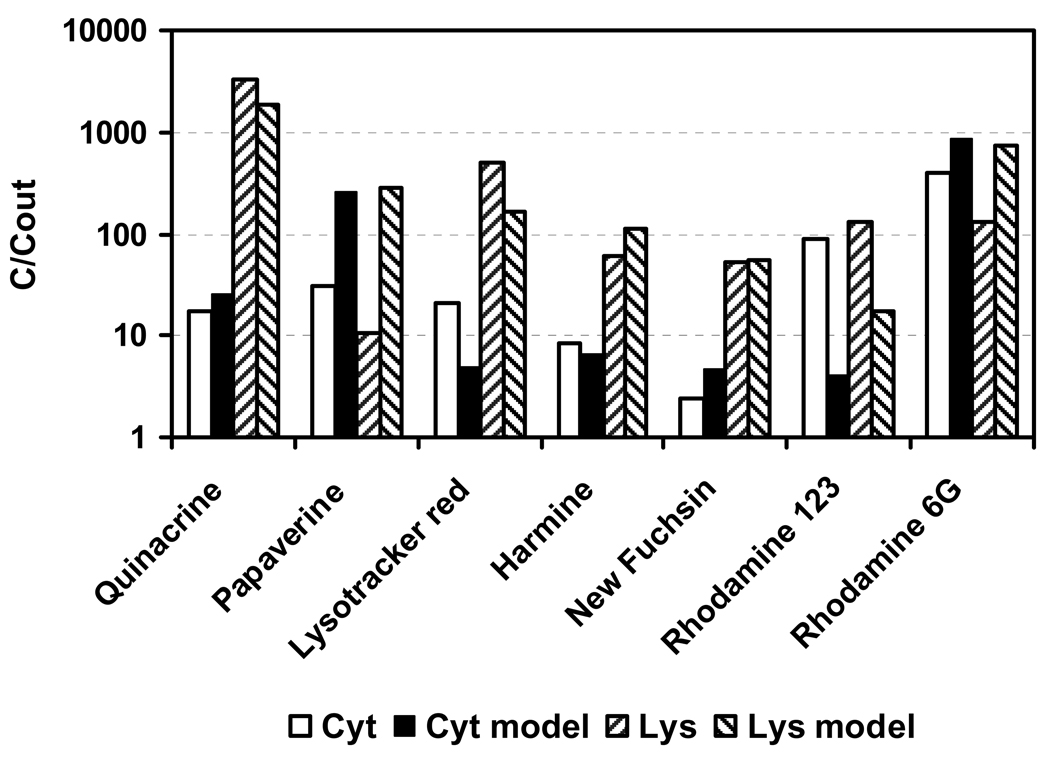
Furthermore, Duvvuri et al. (2004) measured the accumulation of seven bases in human leukemic cells. Raw data were provided by the first author (Duvvuri 2007, personal communication). For the simulation, physico-chemical properties calculated with ACD software package (2007) were used. Four of the compounds are bivalent bases, namely quinacrine, new fuchsine, rhodamine 6G and rhodamine 123, but only quinacrine has pKa-values in the optimum range for lysosomal accumulation predicted by the cell model. The model predicted a very high accumulation in lysosomes (> 1000) and moderate uptake into cytosol (9.3) for quinacrine (QNC). In this experiment, the measured accumulation of QNC in lysosomes was 3320 and 17 in cytosol. Deviations between model and experiment can be seen (Figure 7). For papaverine, the predicted accumulation was much too high. For this compound, the estimated log KOW differs substantially from the measured value in Duvvuri et al. (2004). For rhodamine 123, the prediction failed in tendency and accuracy. The cation and the neutral molecule of rhodamine 123 have very similar octanol-water partition coefficients, and biomembrane permeabilities may also be similar (Duvvuri et al. 2004). If the permeability ratio between neutral molecule and ion is low, no ion trap occurs and the compound does not accumulate in lysosomes (compare Figure 3).
Figure 7.
Comparison of measured (Duvvuri et al. 2004) and modeled (“model”) concentrations of seven basic compounds in cytosol (“Cyt”) and Lysosome (“Lys”).
Drugs _targeting lysosomes
A more practical test of the model is to evaluate whether the chemical properties predicted to give optimal selective accumulation in lysosomes are found with drugs in clinical use. The most serious disease involving lysosomes is malaria (Plasmodium sp.). White (1985) lists twelve compounds tested as antimalarial therapeutical agents, of which ten are active substances. They are listed together with their properties (estimated with ACD or from the literature) in Table 2.
Table 2.
Antimalarial drugs in clinical use (White 1985); properties estimated with ACD (2007); in brackets: Newton and Kluza (1978) or Hansch et al. (1995).
| Chemical | Valency | pKa 1 base |
pKa 2 base |
pKa acid |
log KOW |
Optimum range |
Act as |
|---|---|---|---|---|---|---|---|
| Amodiaquine | +3,−1 | 9.34 | 5.62 | 10.19 | 4.77 | yes | bivalent base |
| Artemesinine | 0 | - | - | - | 2.27 | no | probably metabolised |
| Chloroquine | +2 | 10.47 (9.94) |
6.43 (8.1) |
- | 4.69 (4.38) |
yes | bivalent base |
| Cycloguanil | +2 | 9.27 | −3.55 | - | 1.19 | yes | monovalent base |
| Halofantrine | +1,−1 | 9.49 | 14 | 7.92 | close | monovalent base | |
| Mefloquine | +2,−1 | 10.04 | −2.30 | 12.8 | 2.87 | close | monovalent base |
| Primaquine | +2 | 10.38 | 4.12 | - | 2.67 | close | bivalent base |
| Pyrimethamine | +2 | 6.77 (7.2) | −0.23 | - | 2.45 | yes | monovalent base |
| Quinine | +2,−1 | 9.28 (8.8) |
4.77 (4.2) |
12.8 | 3.44 | yes | bivalent base |
| Quinidine | +2,−1 | (8.34) | (4.21) | 12.8 | 3.44 | yes | bivalent base |
The physico-chemical properties are considered to be in the optimum range predicted by the model when the chemical is either a monovalent base with pKa between 6 and 10 (Figure 2) and log Kow from 0 to 3, or a bivalent base with log KOW between 3 and 6 (Figure 5), pKa 1 (higher pKa) below 10 and pKa 2 above 4 (Figure 4). Chemicals were judged as ”close” to the optimum range when one of these conditions was not fulfilled. Weak acidic groups (pKa 10.2 to 14) of the amphoteric compounds and very weak basic groups (pKa −0.23 to −3.55) of some multivalent bases do not dissociate inside the acidic lysosomes (pH 5), thus these compounds act as mono- or bivalent bases.
Out of the ten active compounds, the properties of six were within the optimum range predicted by the model, and three were close. The pKa-values of the monovalent bases were between 6.77 and 10.04 (optimum range given as 6 to 10), and the log KOW-values were between 1.19 and 2.87 (optimum 0 to 3), disregarding halofantrine, which was not predicted to accumulate selectively in lysosomes by passive diffusion. The pKa-values of the bivalent bases were between 8.34 and 10.38 (pKa 1) and 4.12 and 8.1 (pKa 2), while the predicted optimum range was from 4 to 10. The log KOW-values ranged from 2.67 to 4.77 (predicted optimum range 3 to 6) and were indeed higher as for the monovalent bases. For nine out of the ten antimalarial drugs, the model predicts a higher accumulation in lysosomes than in cytosol (Table 3). In six out of the ten cases, the predicted accumulation in lysosomes is at least 5 times higher than in cytosol or mitochondria (“selective” in bold in Table 3). The compound artemesinine is neutral and thus does not have properties that lead to an accumulation in lysosomes. Perhaps, a metabolite of artemesinine is the active agent. The structure indicates that artemesinine might be rapidly metabolised (Eva M. Seeger, personal communication 2008). This was also observed for proguanil (active metabolite is cycloguanil) (White 1985).
Table 3.
Predicted intracellular localization of ten antimalarial drugs; concentration ratio to outside in lysosomes (Lys), cytosol (Cyt) and mitochondria (Mit); in bold: selective accumulation in lysosomes (> 5times above cytosol and mitochondria).
| Chemical | Lys | Cyt | Mit |
|---|---|---|---|
| Amodiaquine | 479 | 42.5 | 51.2 |
| Artemesinine | 10 | 10 | 10 |
| Chloroquine * | 582 – 5180** | 23 | 2.85 |
| Cycloguanil | 43.5 | 3.4 | 0.5 |
| Halofantrine | 23700 | 18100 | 83300 |
| Quinine | 48.3 | 5.5 | 3.1 |
| Mefloquine | 9.2 | 5.8 | 4.1 |
| Primacrine | 12.5 | 5.5 | 3.4 |
| Pyrimethamine | 72.1 | 12.6 | 12.0 |
| Pyrimethamine* | 127 | 10.3 | 9.2 |
| Quinine * | 138 | 8.7 | 6.4 |
| Quinidine * | 239 | 17.3 | 15.2 |
Calculated with the data provided by Newton and Kluza (1978); quinine and quinidine are structurally identical optical isomeres.
pH of lysosomes 5 or 6; an increase of lysosomal pH has been observed after adding chloroquine to cells (Poole and Ohkuma 1981).
For a successful effect of a drug, a mode of action must be present, but the drug also needs to reach the _target site. It has been frequently stressed in the literature that one weak basic group and moderate lipophilicity is a good preposition for accumulation of drugs in lysosomes (Duvvuri and Krise 2005b, De Duve et al. 1974, Mc Intyre and Cutler 1988, Colombo and Bertini 1988), even though other mechanisms may be involved in accumulation and action. Four of the ten drugs in the dataset indeed act as monovalent weak bases and possess medium lipophilicity (Table 2).
But five of the ten compounds, namely amodiaquine, chloroquine, quinine, quinidine (the stereoisomer of quinine) and primaquine, have two basic pKa constants, and at least one pKa-value of each compound is close to the optimum (pKa at 8) identified by the model. Their lipophilicity is in average 1 1/2log units higher than that of the monovalent basic drugs. Quinacrine, that showed the highest lysosomal accumulation in the experiments of Duvvuri et al. (2004), also fits into this scheme. A potentially high lysosomal accumulation of bivalent bases has been predicted before, but the optimum pKa was assumed at values above 10, and no lipophilicity range was given (McIntyre & Cutler 1988). Thus, so far no predictions have been made that point out that it is the weak bivalent weak bases with moderate to high lipophilicity (log KOW 3 to 6) that possess the highest potential for lysosomal accumulation. This is a fine confirmation for the capability of the model to optimize drug design of lysosome (and other organelle) _targeting molecules.
Limitations of the cell model
Data uncertainty
As for any physical model, there are limitations in the ability of our model to simulate the actual behavior of molecules in living cells. The uncertain accuracy of physicochemical data used to parameterize the model constitutes a mundane limitation. Analogous ambiguities arise with organelles, e.g. what are the appropriate membrane potentials and internal pH values? Such problems, though not conceptually overwhelming, are nevertheless often difficult to deal with. The model in its present form is simplistic, as it considers a ‘generic’ cell. Entry of data for different cell types would increase biological realism.
Feedback mechanisms
The model is linear in its basic structure. Non-linear processes, like saturation effects and precipitation of compounds, and specific processes, such as the sorption of bases to acidic phospholipids (Rodgers et al. 2005), were not taken into consideration. Feedback mechanisms, such as effects of the accumulated molecules on membrane potentials, pH, and organellar volume, are not calculated within the model. However, it is possible to adapt these parameters manually. For example, the intracellular pH can be raised to simulate a buffering effect from the accumulation of bases. Also not considered are toxic effects of compounds accumulating in lysosomes or other organelles.
Active transport
The only transport process considered is passive diffusion. Active transport is not included, so the present model does not account for internalization processes such as endocytosis. Consequently, uptake into lysosomes due to fluid phase and adsorptive endocytosis cannot be anticipated. Nevertheless, the basic equations that constitute the model could be modified. While the present model is limited in scope to permeable, freely soluble molecules, there is no inherent limitation to the inclusion of active transport mechanisms, as well as enzymatic mechanisms (including metabolism) and binding interactions.
Accuracy of pKa optimum ranges
From the Debye-Hückel Theory follows that the ionic strength I of solutions has impact on the pKa. At I = 0.3 M, the apparent pKa of monovalent bases is 0.22 units lower, of acids higher. For bivalent bases and acids, the change is 0.62 units. Several factors change pKa-values obtained experimentally, which have therefore a certain uncertainty and may also differ from estimated values (compare Table 2). Also, inside membranes, the apparent pKa may be different from the value in pure aqueous systems (Newton and Kluza 1978). Tautomeric effects can also impact the dissociation (Rosenberg and Schulman 1978). Taken this together, the optimum pKa-ranges for lysosomal accumulation given in this work may deviate 1 to 2 log units from real optima (which extend more to the stronger end).
Strength of the cell model
Despite the limitations of the modeling approach, this cellular pharmacokinetic model shows considerable promise as a tool for studying the physicochemical properties leading to greatest accumulation in lysosomes relative to other organelles, i.e. for drug design. Until now, quantitative structure-activity relationship (QSAR) approaches have been used to predict intracellular localization of molecules. Based on empirical knowledge, QSAR approaches are powerful predictive tools. Complementing QSAR methods, the present model can give numerical values (i.e. concentrations) and information about kinetics (i.e., the time required to reach a concentration) (Horobin et al. 2007).
Model availability
The model is freely available as a user-friendly and unprotected excel spread-sheet version from the corresponding author (email to: stt@env.dtu.dk).
Acknowledgements
We wish to acknowledge Prof. W. Martin at the Division of Neuroscience & Biomedical Systems, IBLS, University of Glasgow for providing facilities to one of us (RWH). The study was partly funded by the European Commission, 6th Framework program, project OSIRIS [GOCE contract number 037017]. G. R. Rosania would like to acknowledge financial support from NIH grants RO1-GM078200 and P20-HG003890. Antonio Franco assisted with the ACD calculations. Thanks to Muraliskrishna Duvvuri for providing raw data of experiments.
Contributor Information
Stefan Trapp, Email: stt@env.dtu.dk.
Gus R. Rosania, Email: grosania@umich.edu.
Richard W. Horobin, Email: RichardWHorobin@tomcroy.co.uk.
Johannes Kornhuber, Email: johannes.kornhuber@ukerlangen.de.
REFERENCES
- ACD Advanced Chemistry Development Inc. ACD/LogD Suite version 10.02. Toronto, Canada: 2007. [last accessed 12th April 2008]. http://www.acdlabs.com/ [Google Scholar]
- Appelo CAJ, Postma D. Geochemistry and groundwater pollution. 4th Ed. Rotterdam, NL: Balkema; 1999. [Google Scholar]
- Briggs GE, Hope AB, Robertson RN. Electrolytes and plant cells. In: James WO, editor. Botanical monographs. vol. 1. Oxford, UK: Blackwell Scientific; 1961. [Google Scholar]
- Briggs GG, Rigitano RLO, Bromilow RH. Physico-chemical factors affecting uptake by roots and translocation to shoots of weak acids in barley. Pestic Sci. 1987;19:101–112. [Google Scholar]
- Chen VY, Rosania GR. The great multidrug-resistance paradox. ACS Chem Biol. 2006;1:271–273. doi: 10.1021/cb600215q. [DOI] [PubMed] [Google Scholar]
- Colombo MI, Bertini F. Properties of binding sites for chloroquine in liver lysosomal membranes. J Cell Physiol. 1988;137:598–602. doi: 10.1002/jcp.1041370330. [DOI] [PubMed] [Google Scholar]
- Debye P, Hückel E. Zur Theorie der Elektrolyte. Z Physikal Chem. 1923;24:185–206. [Google Scholar]
- De Duve C, De Barsy T, Poole B, Trouet A, Tulkens P, Van Hoof F. Commentary. Lysosomotropic agents. Biochemical Pharmacology. 1974;23:2495–2531. doi: 10.1016/0006-2952(74)90174-9. [DOI] [PubMed] [Google Scholar]
- Duvvuri M, Gong Y, Chatterji D, Krise JP. Weak base permeability characteristics influence the intracellular sequestration site in the multidrug-resistant human leukemic cell line HL-60. J Biol Chem. 2004;279:32367–32372. doi: 10.1074/jbc.M400735200. [DOI] [PubMed] [Google Scholar]
- Duvvuri M, Krise JP. Intracellular drug sequestration events associated with the emergence of multidrug resistance: a mechanistic review. Front Biosci. 2005;10:1499–1509. doi: 10.2741/1634. [DOI] [PubMed] [Google Scholar]
- Duvvuri M, Krise JP. A novel assay reveals that weakly basic model compounds concentrate in lysosomes to an extent greater than pH-partitioning theory would predict. Molecular Pharmaceutics. 2005b;2:440–448. doi: 10.1021/mp050043s. [DOI] [PubMed] [Google Scholar]
- Duvvuri M, Konkar S, Funk RS, Krise JM, Krise JP. A chemical strategy to manipulate the intracellular localization of drugs in resistant cancer cells. Biochemistry. 2005;44:15743–15749. doi: 10.1021/bi051759w. [DOI] [PubMed] [Google Scholar]
- Duvvuri M, Konkar S, Hong KH, Blagg BSJ, Krise JP. A new approach for enhancing differential selectivity of drugs to cancer cells. ACS Chemical Biology. 2006;1:309–315. doi: 10.1021/cb6001202. [DOI] [PubMed] [Google Scholar]
- Ginsburg H, Ward SA, Bray PG. An integrated model of chloroquine action. Parasitol Today. 1999;15:357–360. doi: 10.1016/s0169-4758(99)01502-1. [DOI] [PubMed] [Google Scholar]
- Goldman DE. Potential, impedance and rectification in membranes. J Gen Physiol. 1943;27:37–60. doi: 10.1085/jgp.27.1.37. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hansch C, Leo A, Hoekman D. Exploring QSAR: Fundamentals and applications in chemistry and biology. Washington DC: American Chemical Society; 1995. [Google Scholar]
- Henderson LJ. Concerning the relationship between the strength of acids and their capacity to preserve neutrality. J Physiol. 1908;21:173–179. [Google Scholar]
- Hodgkin AL, Katz B. The effect of sodium ions on the electrical activity of the giant axon of the squid. J Physiol. 1949;108:37–77. doi: 10.1113/jphysiol.1949.sp004310. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Horobin RW, Stockert JC, Rashid-Doubell F. Fluorescent cationic probes for nuclei of living cells: why are they selective? A quantitative structure–activity relations analysis. Histochem Cell Biol. 2006;126:165–175. doi: 10.1007/s00418-006-0156-7. [DOI] [PubMed] [Google Scholar]
- Horobin RW, Trapp S, Weissig V. Mitochondriotropics: A review of their mode of action, and their applications for drug and DNA delivery to mammalian mitochondria. J Contr Release. 2007;121:125–136. doi: 10.1016/j.jconrel.2007.05.040. [DOI] [PubMed] [Google Scholar]
- Ishizaki J, Yokogawa K, Ichimura F, Ohkuma S. Uptake of imipramine in rat liver lysosomes in vitro and its inhibition by basic drugs. J Pharmacol Exp Therapeutics. 2000;294:1088–1098. [PubMed] [Google Scholar]
- Kaufmann AM, Krise JP. Lysosomal sequestration of amine-containing drugs: Analysis and therapeutic implications. J Pharm Sci. 2007;96:729–746. doi: 10.1002/jps.20792. [DOI] [PubMed] [Google Scholar]
- Kornhuber J, Medlin A, Bleich S, Jendrossek V, Henkel AW, Wiltfang J, Gulbins E. High activity of acid sphingomycelinase in major depression. J. Neural Transmission. 2005;112:1583–1590. doi: 10.1007/s00702-005-0374-5. [DOI] [PubMed] [Google Scholar]
- Kornhuber J, Tripal P, Reichel M, Bleich S, Wiltfang J, Gulbins E. Identification of new functional inhibitors of acid sphingomyelinase using a quantitative structure-activity relations model. J Med Chem. 2008;51:219–237. doi: 10.1021/jm070524a. [DOI] [PubMed] [Google Scholar]
- Lemieux B, Percival MD, Falgueyret J. Quantification of the lysosomotropic character of cationic amphiphilic drugs using the fluorescent basic amine Red DND-99. The Journal of Pharmacology and Experimental Therapeutics. 2004;294:247–251. doi: 10.1016/j.ab.2004.01.010. [DOI] [PubMed] [Google Scholar]
- MacIntyre AC, Cutler DJ. The potential role of lysosomes in tissue distribution of weak bases. Biopharmaceutics & drug disposition. 1988;9:513–526. doi: 10.1002/bod.2510090602. [DOI] [PubMed] [Google Scholar]
- Newton DW, Kluza RB. pKa values of medicinal compounds in pharmacy practice. Drug Intelligence and Clinical Pharmacy. 1978;12:547–554. [Google Scholar]
- Ohkuma S, Poole B. Fluorescence probe measurement of the intralysosomal pH in living cells and the perurbation of pH by various agents. Proc Natl Acad Sci USA. 1978;75:3327–3331. doi: 10.1073/pnas.75.7.3327. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Poole B, Ohkuma S. Effect of weak bases on the intralysosomal pH in mouse peritoneal macrohages. J Cell Biol. 1981;90:665–669. doi: 10.1083/jcb.90.3.665. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raven JA. Transport of indolacetic acid in plant cells in relation to pH and electrical potential gradients, and its significance for polar IAA transport. New Phytol. 1975;74:163–172. [Google Scholar]
- Rashid F, Horobin RW. Accumulation of fluorescent non-cationic probes in mitochondria of cultured cells: observations, a proposed mechanism and some implications. J Microsc. 1991;163:233–241. doi: 10.1111/j.1365-2818.1991.tb03175.x. [DOI] [PubMed] [Google Scholar]
- Rodgers T, Leahy D, Rowland M. Physiologically based pharmacokinetic modeling: Predicting the tissue distribution of moderate-to-strong bases. J Pharmaceut Sci. 94:1259–1276. doi: 10.1002/jps.20322. [DOI] [PubMed] [Google Scholar]
- Rosenberg LS, Schulman SG. Tautomerism of singly protonated chloroquine and quinacrine. J Pharmaceut Science. 1978;67:1770–1772. doi: 10.1002/jps.2600671239. [DOI] [PubMed] [Google Scholar]
- Saparov SM, Antonenko YM, Pohl P. A new model of weak acid permeation through membranes revisited: Does Overton still rule? Biophys. J. Biophys. Lett. doi: 10.1529/biophysj.106.084343. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Slater AF. Chloroquine: mechanism of drug action and resistance in Plasmodium falciparum. Pharmacol Ther. 1993;57:203–235. doi: 10.1016/0163-7258(93)90056-j. [DOI] [PubMed] [Google Scholar]
- Sugioka Y, Suzuki M, Sugioka K, Nakano M. A ferriprotoporphyrin IX-chloroquine complex promotes membrane phospholipid peroxidation. A possible mechanism for antimalarial action. FEBS Lett. 1987;223:251–254. doi: 10.1016/0014-5793(87)80299-5. [DOI] [PubMed] [Google Scholar]
- Trapp S. Plant uptake and transport models for neutral and ionic chemicals. Environ Sci&Pollut Res. 2004;11:33–39. doi: 10.1065/espr2003.08.169. [DOI] [PubMed] [Google Scholar]
- Trapp S, Horobin RW. A predictive model for the selective accumulation of chemicals in tumor cells. Eur Biophys J. 2005;34:959–966. doi: 10.1007/s00249-005-0472-1. [DOI] [PubMed] [Google Scholar]
- White NJ. Clinical pharmacokinetics of antimalarial drugs. Clinical pharmacokinetics. 1985;10:187–215. doi: 10.2165/00003088-198510030-00001. [DOI] [PubMed] [Google Scholar]
- Van Dyke RW. Proton pump-generated electrochenical gradients in rat liver multivesicular bodies. J Biol Chem. 1988;263:2603–2611. [PubMed] [Google Scholar]
- Zhang J, Krugliak M, Ginsburg H. The fate of ferriprotorphyrin IX in malaria infected erythrocytes in conjunction with the mode of action of antimalarial drugs. Mol Biochem Parasitol. 1999;99:129–141. doi: 10.1016/s0166-6851(99)00008-0. [DOI] [PubMed] [Google Scholar]
- Zhang X, Shedden K, Rosania GR. A cell-based molecular transport simulator for pharmacokinetic prediction and cheminformatic exploration. Mol Pharm. 2006;3:704–716. doi: 10.1021/mp060046k. [DOI] [PMC free article] [PubMed] [Google Scholar]