Adaptive System Identification for Estimating Future Glucose Concentrations and Hypoglycemia Alarms

Meriyan Eren-Oruklu; Ali Cinar; Derrick K Rollins; Lauretta Quinn

doi:10.1016/j.automatica.2012.05.076

. Author manuscript; available in PMC: 2013 Aug 1.

Published in final edited form as: Automatica (Oxf). 2012 Jun 22;48(8):1892–1897. doi: 10.1016/j.automatica.2012.05.076

Adaptive System Identification for Estimating Future Glucose Concentrations and Hypoglycemia Alarms

Meriyan Eren-Oruklu ^a, Ali Cinar ^a,^*, Derrick K Rollins ^b, Lauretta Quinn ^c

PMCID: PMC3409594 NIHMSID: NIHMS389282 PMID: 22865931

Abstract

Many patients with diabetes experience high variability in glucose concentrations that includes prolonged hyperglycemia or hypoglycemia. Models predicting a subject’s future glucose concentrations can be used for preventing such conditions by providing early alarms. This paper presents a time-series model that captures dynamical changes in the glucose metabolism. Adaptive system identification is proposed to estimate model parameters which enable the adaptation of the model to inter-/intra-subject variation and glycemic disturbances. It consists of online parameter identification using the weighted recursive least squares method and a change detection strategy that monitors variation in model parameters. Univariate models developed from a subject’s continuous glucose measurements are compared to multivariate models that are enhanced with continuous metabolic, physical activity and lifestyle information from a multi-sensor body monitor. A real life application for the proposed algorithm is demonstrated on early (30 min in advance) hypoglycemia detection.

Keywords: Modeling and identification, Parameter and state estimation, Identification algorithms, Recursive estimation

1. Introduction

Patients with diabetes control their glucose levels through lifestyle modifications and, if required, with oral anti-diabetic medicines and insulin analogs. Success rate at achieving normoglycemia with current diabetes management has been low, and patients may experience prolonged hyper-(high) or hypoglycemic (low glucose) episodes. The main reason is that patients have difficulty in predicting future glucose concentrations and therefore determining the required corrective action.

Reliable glucose prediction models have the potential to significantly improve the management of diabetes. Future glucose levels can be used to provide an early alarm that predicts hypoglycemia, allowing the necessary time for the patient to prevent the incident (Knobbe, 2005; Palerm, 2007; Buckingham, 2009; Eren-Oruklu, 2010). The fully-automated artificial pancreas with closed-loop administration of insulin will also require a model for prediction of blood glucose concentrations as a component of its control algorithm (Hovorka, 2004; Eren-Oruklu, 2009b).

This paper presents a subject-specific glucose prediction model that is developed by using measurements from a glucose sensor and metabolic, physical activity and lifestyle information from a multi-sensor armband. The frequent data from the sensors are analyzed by time-series methods. Other studies that focus on time-series approach for modeling glucose dynamics include Finan (2006), Van Herpe (2006), and Sparacino (2007). The first two approaches require manually entered inputs such as insulin infusion rate, meal information and insulin resistance. Similarly, other empirical models proposed in the literature require manual inputs (Bellazzi, 2000; Katayama, 2004; Yamaguchi, 2006), or training data for model development (Mougiakakou, 2000; Florian, 2005; Zainuddin, 2009). The algorithm discussed in this paper does not require any training data or manual inputs from patients.

We have previously developed subject-specific models that utilize only recent glucose history from a continuous glucose monitoring (CGM) device, with 3–5% error for 30 min ahead prediction (Eren-Oruklu, 2009a). In this work we extend the model to include the effect of a subject’s physical activity and emotional stimuli such as stress on glucose metabolism. Physiological measurements from a multi-sensor body monitor are used. Such physiological signals will supplement the CGM information and enhance the prediction accuracy of the glucose predicting models. Even though activity and stress levels are known to have a significant effect on subject’s whole-body fuel metabolism, only a few studies are available in literature that focus on glucose homoeostasis during exercise or stress (Derouich, 2002; Kim, 2007; Roy, 2008; Rollins, 2009; Valletta, 2009).

The paper is organized as follows. Section 2 introduces univariate (glucose only) and multivariate (glucose and physiological signals) models that describe a subject’s glucose metabolism. In Section 3, we present a recursive algorithm for estimating the model parameters. Performance analysis of the proposed univariate and multivariate algorithms are compared in Section 4 and application to early hypoglycemia detection is presented in Section 5.

2. System Modeling

Glucose dynamics show great variability from subject to subject. Metabolic changes that are caused by stress, illness or changes in insulin sensitivity may also lead to variation in glucose metabolism within the same subject. A reliable model for predicting future glucose concentrations should address such variabilities and should be able to adapt to unexpected glycemic perturbations, in other words, be subject-specific. For many modeling strategies this will require a prior examination of experimental data from each individual studied, and therefore may limit the strategy from being implemented in a home-use device.

We utilize time-series methods to analyze the discrete time data from two sensors and develop empirical subject-specific linear models. A subject’s own glucose sensor and armband data are used for model development. Measurements at a high frequency (5 min sampling time) provide more insight not only into the subject’s glucose profile throughout the day, but also into the rate at which glucose variations occur and the effect of physiological signals on these variations.

Univariate Model

The univariate glucose model is developed using only CGM device data. The observed behavior can be described with autoregressive moving average (ARMA) time series model:

y_{k} = a_{1, k} y_{k - 1} + \dots + a_{n_{A}, k} y_{k - n_{A}} + ε_{k} + c_{1, k} ε_{k - 1} + \dots + c_{n_{C}, k} ε_{k - n_{C}}

(1)

k indicates the current sampling instant. {y_k, …, y_k–nA} is the sequence of current and past glucose measurements and the sequence {ε_k, …, ε_k–nC} represents white noise. a_i,k and c_i,k are the unknown and time-varying model parameters, and n_A and n_C indicates the model order.

Multivariate Model

Food intake, physical activity, emotional stimuli and lifestyle have significant effects on glucose metabolism and daily glucose excursions. Exercise can increase or decrease in glucose levels depending on the patient’s eating history (Rollins, 2009). Physiological measurements from a multi-sensor body monitor will supplement the CGM information and can be used to enhance the univariate glucose model.

Multiple variables observed simultaneously with a CGM sensor and an armband are used to form a multivariate time series model. The autoregressive moving average with exogenous inputs (ARMAX) model which has multiple inputs is described as:

\begin{array}{l} y_{k} = a_{1, k} y_{k - 1} + \dots + a_{n_{A} k} y_{k - n_{A}} \\ + b_{0, k}^{(1)} u_{k - d^{(1)}}^{(1)} + \dots + b_{n_{B}, k}^{(1)} u_{k - d^{(1)} - {n_{B}}^{(1)}}^{(1)} \\ + \dots \\ + b_{0, k}^{(n)} u_{k - d^{(n)}}^{(n)} + \dots + b_{n_{B}, k}^{(n)} u_{k - d^{(n)} - {n_{B}}^{(n)}}^{(n)} \\ + ε_{k} + c_{1, k} ε_{k - 1} + \dots + c_{n_{C}, k} ε_{k - n_{C}} \end{array}

(2)

where y_k is the subject’s glucose concentration. The physiological signals from the armband forms the model inputs {u⁽¹⁾_k, …, u(n)_k}, and ε_k denotes the noise term. Compared to (1), additional model parameters for the multi-input ARMAX model are b⁽ⁱ⁾_j,k with i = 1,…,n and j = 1,…,n_B(i). n denotes the total number of inputs and n_B(i) is the model order of ith input. d⁽ⁱ⁾ introduces d-steps of delay to the ith input to account for possible delay in input action.

3. Parameter Estimation

A reliable model should be able to capture the variation in glucose metabolism of the subject with changing daily life conditions. We recursively identify the model parameters at each sampling step to include the information from new measurements. In addition, for a faster adaptation in case of drastic glycemic disturbance, we use a parameter change detection strategy that is included in the identification algorithm.

3.1. Recursive Least Squares

The time-varying parameters of (1) or (2) are recursively identified at each sampling step. Weighted recursive least squares (RLS) is used for on-line identification. For a given model order (n_A, n_B⁽ⁱ⁾, and n_C), the RLS provides the estimate of model parameters that minimize the squared error between the observed and estimated variables.

The time series models (1) or (2) can be rewritten in linear regression form:

y_{k} = ϕ_{k - 1}^{T} {\hat{θ}}_{k - 1} + e_{k} = {\hat{y}}_{k} + e_{k}

(3)

where y_k and ŷ_k represent the actual observation of the system and its model estimated value at kth sampling instant, respectively. e_k denotes the residual terms caused by difference between subject’s behavior and its model. ϕ_k–1 denotes the vector of historical observations and θ̂_k_–l is the estimate of time-varying vector containing model parameters. For the multivariate model of (2), ϕ_k–1 and θ̂_k_–l are:

ϕ_{k - 1} = {[y_{k - 1} \dots y_{k - n_{A}} \dots u_{k - d^{(i)}}^{(i)} \dots u_{k - d^{(i)} - {n_{B}}^{(i)}}^{(i)} \dots e_{k - 1} \dots e_{k - n_{C}}]}^{T}

(4)

{\hat{θ}}_{k - 1} = {[{\hat{a}}_{1, k - 1} \dots {\hat{a}}_{n_{A}, k - 1} \dots {\hat{b}}_{0, k - 1}^{(i)} \dots {\hat{b}}_{n_{B}, k - 1}^{(i)} \dots {\hat{c}}_{1, k - 1} \dots {\hat{c}}_{n_{C}, k - 1}]}^{T}

(5)

Representation of the vectors ϕ_k_–1 and θ̂_k_–l for the univariate model of (1) is straightforward, as it only requires exclusion of input related terms (u⁽ⁱ⁾_k–j and b⁽ⁱ⁾_j,k–1).

The weighted RLS algorithm that estimates the model parameters is given by:

{\hat{θ}}_{k} = {\hat{θ}}_{k - 1} + K_{k} e_{k} = {\hat{θ}}_{k - 1} + K_{k} {y_{k} - ϕ_{k - 1}^{T} {\hat{θ}}_{k - 1}}

(6)

K_{k} = \frac{P_{k - 1} ϕ_{k - 1}}{λ + ϕ_{k - 1}^{T} P_{k - 1} ϕ_{k - 1}}

(7)

P_{k} = \frac{1}{λ} [P_{k - 1} - \frac{P_{k - 1} ϕ_{k - 1} ϕ_{k - 1}^{T} P_{k - 1}}{λ + ϕ_{k - 1}^{T} P_{k - 1} ϕ_{k - 1}}]

(8)

K_k and P_k in (7) and (8) denote the vector of estimator gains and the estimate of error variance matrix, respectively. λ is the forgetting factor (0 < λ ≤ 1).

3.2. Change Detection

The RLS with a constant λ will normally provide sufficient model tracking unless the system deviates from its steady state operating conditions. However, for some systems, as is with glucose dynamics, normal operating conditions may include large transition periods. To obtain quick model tracking under such deviations, a small value of λ is required, to discard the old information. On the other hand, when the system returns to its near steady state conditions, the small λ will lead to increase in the error variance, P_k in (8), which in time may cause numerical instability.

Since daily glucose excursions include large transition periods (e.g. after a meal consumption), we propose to use a variable λ that takes a small value during transition periods (change detected) and a large value during fasting conditions. A number of variable forgetting factor algorithms have been developed in the literature (Haykin, 1996; Song, 200; Leung, 2005). They mostly focus on the squared error or covariance matrix to vary λ, and therefore, are sensitive to the level and character of the measurement noise. We propose a mechanism for varying λ with a change detection strategy integrated to the RLS algorithm that monitors the variation in the model parameters. When the algorithm detects a change in parameters, the value of λ in the RLS is reduced. The proposed change detection method is described by null and alternative hypotheses given by:

\begin{array}{l} H_{0} : E ({\hat{θ}}_{k}) = {\hat{Θ}}_{N}, for N < k < N + N_{W} \\ H_{1} : E ({\hat{θ}}_{k}) \neq {\hat{Θ}}_{N}, for N < k < N + N_{W} \end{array}

(9)

E (θ̂_k) describes the expected value of parameter estimates at kth sampling instant, and Θ̂_N is the expected value computed using the data until time instant N. To avoid changes due to non-persistent abnormalities in the data such as sensor noise, the value of λ is not reduced at the first instant of change detection. Instead, consistency of the change for several time steps (window size, N_W) is assured first. When a persistent change with the duration of the window size is detected, λ is reduced to a smaller value and Θ̂_N is replaced with its new estimate.

4. Results

4.1. Subject Data

Data used in this study consists of glucose concentration and physiological signals collected from 5 subjects with type 2 diabetes under free living conditions (23.8±2.4 days of data per subject). A Medtronic MiniMed Continuous Glucose Monitor, MMT-7012 (Medtronic MiniMed, Northridge, CA) was used to gather the glucose data. This device measures subcutaneous glucose concentrations every five minutes. The body monitoring system SenseWear Pro3 (BodyMedia Inc., Pittsburgh, PA) was used for collection of metabolic, physical activity and lifestyle information. The armband weights 80 g and is worn on the upper right arm without obstructing daily activities. It provides seven signals to describe the subject’s activity and emotional conditions: energy expenditure (EE), average longitudinal acceleration (LA), transverse acceleration peaks, transverse acceleration mean of absolute difference, near-body temperature (BT), heat flux (HF) and galvanic skin response (GSR). The SenseWear monitor provides measurements every minute, therefore, the physiological data were trimmed to include the data points at the same time instants as those from the glucose monitor.

4.2. Predicting Future Glucose Concentrations

After identification of the model parameters at each step using weighted RLS (6)–(8) and the change detection method (9), the univariate model in (3) (now with known parameters) is easily appended m-steps into the future to predict the future excursion of glucose concentrations (ŷ_{k+m|k;θcirc;_k}) which will be a linear function of current (y_k) and past (y_k-i) glucose measurements. Use of the multivariate model of (2) m-steps into the future requires future values of the exogenous inputs (u⁽ⁱ⁾_k+j) which are unknown until new measurements become available. We assume that input variables, U_k = [u(1)_k … u⁽ⁿ⁾_k]^T, follow a vector ARMA model of orders n_A and n_C (without loss of generality, n_A and n_C can be taken to be the same as in (1)):

U_{k} = \sum_{i = 1}^{n_{A}} A_{i, k} U_{k - i} + \sum_{i = 1}^{n_{c}} C_{i . k} ε_{k - i} + ε_{k}

(10)

where U_k = [u⁽¹⁾_k… u⁽ⁿ⁾_k]^T and ε_k = [ε ⁽¹⁾_k … ε⁽ⁿ⁾_k]^T are considered the system output and the noise vectors of length n, respectively. A_i,k and C_i,k are the m × m matrices composed of model parameters at sampling step k:

A_{i, k} {[\begin{matrix} a_{11, i} & \dots & a_{1 m, i} \\ ⋮ & ⋱ & ⋮ \\ a_{m 1, i} & \dots & a_{m m, i} \end{matrix}]}_{k} C_{i, k} = {[\begin{matrix} c_{11, i} & \dots & c_{1 m, i} \\ ⋮ & ⋱ & ⋮ \\ c_{m 1, i} & \dots & c_{m m, i} \end{matrix}]}_{k}

(11)

4.3. Prediction Performance

The first step is to determine the model orders. Using the data from the CGMS and SenseWear armband, we developed various ARMA (1) and multivariate ARMAX (2) models of different structures (different variable combinations) and different orders (n_A, n_C, n_B). Model order selection was performed for constant parameters case where models are compared based on Akaike information criterion (AIC) over the entire data.

MATLAB System Identification Toolbox (The Math Works Inc., Natick, MA) was used for model order selection. For the univariate ARMA model (1), n_A = 2 and n_C = 1 provide the best model (lowest AIC value). For the multivariate ARMAX model (2), 5 of the 7 signals from the armband have significant contribution to the glucose excursions: EE, LA, HF, GSR and BT. The multivariate model order is n_A = 2, n_B = [1, 1, 2, 2, 2] and d = [4, 4, 5, 7, 5] for the input vector U = [EE, LA, HF, GSR, BT], and n_C = 1. Next, we implemented the recursive identification algorithm for models with the determined orders. The total number of model parameters need to be identified are 3 and 11 for the univariate and multivariate models, respectively. At each sampling step, the model parameters are identified using (6)–(9). Then with known parameter values, the univariate and multivariate models are appended for m-steps to compute the m-step-ahead predicted glucose concentration. Initial value for parameter vector, θ̂_k₌₀ in (6), is assigned zero.

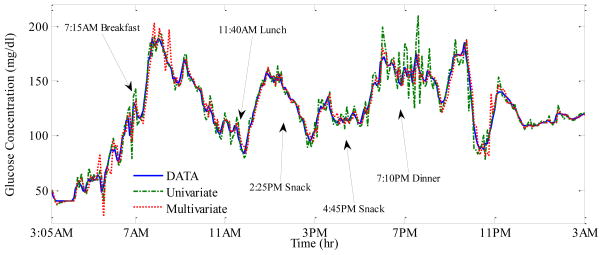
Figure 1 illustrates a typical day for one of the subjects. The proposed algorithm is implemented at the start of that day (3:05AM) with N_W = 5 steps, λ = 0.5 and θ̂_k₌₀ = 0 (untuned model), meaning that no prior data was used for tuning the model. In Figure 1, demonstrated are 30 min ahead predicted glucose values for both multivariate and univariate models. It takes longer for the multivariate model to tune to true patient dynamics (oscillations in the first hours), since it requires identification and convergence of a larger number of model parameters (11 versus 3). However, after the initial tuning period, predictions with the multivariate model follow the CGMS measurements more closely compared to the univariate model. This confirms that physiological signals supplement the CGM information and enhance the prediction accuracy (also Table 1).

Fig. 1 — Glucose prediction with multivariate and univariate models for a typical 24 h period of one of the subjects.

Table 1.

Prediction performance (30 min ahead): Reported are mean values with standard deviations given in parentheses.

	Univariate Model	Multivariate Model
RAD (%)	5.77 (7.18)	4.24 (5.14)
SSGPE (%)	8.81	7.43

Open in a new tab

Prediction performance is numerically evaluated using two error metrics that describe the deviation of the m-step-ahead predicted values (ŷ_{k|k–m;θcirc;_k–m}) from the actual CGMS data (y_k): the relative absolute deviation (RAD) and the sum of squares of the glucose prediction error (SSGPE).

RAD (%) = \frac{| y_{k} - {\hat{y}}_{k ∣ k - m; {\hat{θ}}_{k - m}} |}{y_{k}} \times 100

(12)

SSGPE (%) = \sqrt{\frac{\sum {(y_{k} - {\hat{y}}_{k ∣ k - m; {\hat{θ}}_{k - m}})}^{2}}{\sum y_{k}^{2}}} \times 100

(13)

Table 1 presents the prediction performance of the proposed algorithm over the entire study. Results are for 30 min ahead prediction (m = 6 steps) with N_W = 5 steps (25 min) and λ = 0.5. The forgetting factor is reduced to 0.005 in case of change detection. Prediction accuracy is improved and errors metrics are reduced with the multivariate model.

5. Application: Early Hypoglycemia Detection

Avoiding hypoglycemia while keeping glucose within the narrow normoglycemic range (70–120 mg/dl) is a major challenge for patients with diabetes. Many patients from nocturnal hypoglycemia. Glucose concentrations below 40 mg/dl cause severe impairment in the nervous system that have the potential to lead to seizure, diabetic coma and eventually death.

Some of the CGM sensors available in the market provide a hypoglycemic alarm when the measured glucose decreases below a user specified threshold. However, patients will benefit more from an early alarm that predicts the hypoglycemic episode before it occurs, providing time for corrective action to be taken. A few of the available CGM sensors provide such early alarms by linear extrapolation of the rate of change of glucose concentration into the future (Bode, 2004; DirecNet, 2004; Weinstein, 2007). In contrast, our algorithm is based on future glucose concentration predictions by using more reliable subject-specific and dynamic models that utilize glucose measurement data and physiological signals from an armband.

The multivariate glucose prediction algorithm is used to predict future hypoglycemic episodes before they occur. When the m-step-ahead predicted glucose level is below an assigned threshold value for hypoglycemia (e.g. 60 mg/dl), an alarm is be triggered at that sampling instant, k. The alarm signifies that the patient will experience a hypoglycemia m-steps-ahead from the current time, k.

The prediction of hypoglycemia (alarm issued) is considered false positive if the reference blood glucose measurement at time step k+m is above the defined threshold, and true positive if it is below the threshold value. False negative occurs when alarm is not issued at the kth step (hypoglycemia not predicted), but the reference glucose at step k+m is actually below the threshold value.

Out of total 34330 sampling steps, subjects experienced hypoglycemia (measured glucose below and equal to 60 mg/dl) during 194 steps. Rate of hypoglycemia was low since subjects have type 2 diabetes, and therefore have an active glucagon response to reduce the chance of hypoglycemia. Of these 34330 decisions, 34071 are true negative (alarm not-issued correctly), 144 true positive (alarm issued correctly), 50 false negative (missed alarm), and 65 false positive (alarm issued incorrectly). Sensitivity to detect early hypoglycemia defined as probability of true positive alarms among all hypoglycemic events occurred is 74% with a false alarm rate of 31% (probability of false alarms among all hypoglycemic alarms triggered; false alarm rate = false positive/[false positive + true positive]).

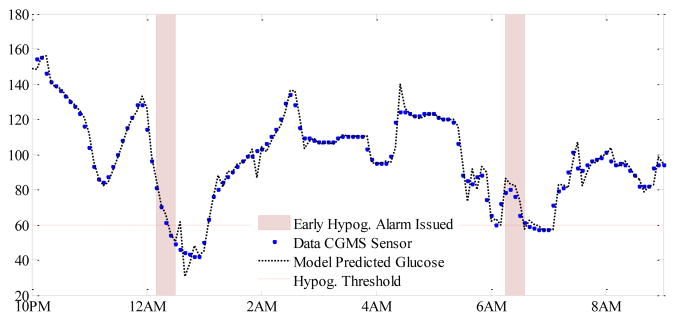
Figure 2 demonstrates a portion of the data when one of the subjects experiences hypoglycemia. Shown are the actual CGMS sensors measurements and 30 min ahead predicted glucose values (with the multivariate model). The red-shaded area in the figure represents the period of early alarms that predicts an incidence of hypoglycemia within the next 30 min. The patient experiences two nocturnal hypoglycemic episodes, each correctly alarmed 30 min before their occurrences. Each alarm lasted for 20 min.

Fig. 2 — *Early* hypoglycemic alarms with the proposed multivariate algorithm for 30 min ahead prediction.

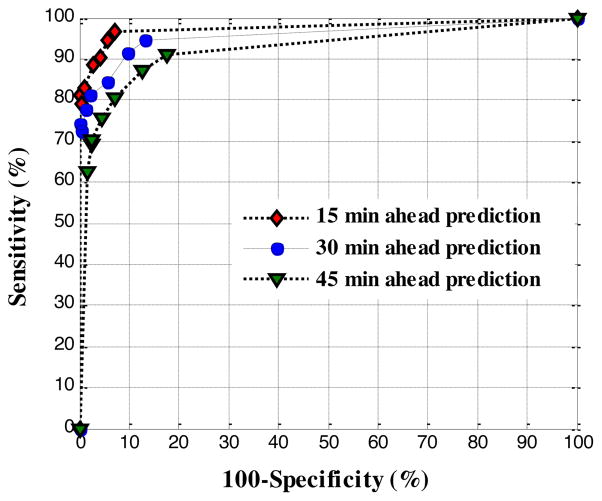
The threshold value selected for hypoglycemia has a significant effect on alarm performance. Increasing the threshold will improve the sensitivity of the alarms to detect hypoglycemia, but at a cost of decreased specificity (a measure used to correctly identify the absence of hypoglycemic events). Another parameter that affects the alarm performance is the prediction horizon (PH). The sensitivity can further be improved by reducing the PH. However, PH should extend long enough to ensure the time for the necessary intervention (e.g. food ingestion) to avoid hypoglycemia. Figure 3 demonstrates the receiver operating characteristic (ROC) curves for 15, 30 and 45 min ahead predictions. The markers on each ROC curve correspond to a different threshold (at 10 mg/dl intervals); with the lowest sensitivity at 60 mg/dl and the highest at 120 mg/dl.

Fig. 3 — ROC curves for prediction horizon of 15, 30 and 45 minutes. Hypoglycemia thresholds are increased at 10 mg/dl intervals in the range of 60–120 mg/dl. Sensitivity = TruePositive/(TruePositive + FalseNegative), Specificity = TrueNegative/(TrueNegative + FalsePositive).

6. Conclusions

We extended our univariate modeling algorithm for predicting glucose concentrations (Eren-Oruklu, 2009a) to a multivariate model that uses not only the subject’s glucose measurements from a CGM device, but also several physiological signals depicting a subject’s physical activity and emotional conditions that have a significant effect on glucose metabolism. Results showed that prediction error (RAD and SSGPE) is significantly reduced with additional measurements from the armband. The modeling algorithm proposed is subject-specific and captures inter- or intra-subject variability. It does not require any prior experimental data, tuning for each subject, or disturbance (meal) information. The algorithm was also successfully implemented for predicting hypoglycemia 30 minutes in advance, with early alarms.

The model are developed and evaluated with data for about 24 days each from 5 subjects with type 2 diabetes. In future research, it could be examined on a larger population and a population with type 1 diabetes. However, the latter will require a more comprehensive model that includes insulin as an additional input. Such a model may further be integrated to a model-based predictive controller to provide closed-loop insulin delivery. Site of insulin infusion, CGM devices with different sampling frequencies, and rejection of large disturbances (i.e. food consumption) are only a few of the key components that a controller should consider before it is employed in any clinical study.

Acknowledgments

This work was partially supported by NIH Grant Nos. DK 085611-01 and DK 20595-32 2 P60.

Biographies

graphic file with name nihms389282b1.gif

Meriyan Eren-Oruklu received her B.Sc. and M.Eng. degrees in Chemical Engineering from the Bogazici University, Istanbul, Turkey in 2003, and the Illinois Institute of Technology, Chicago in 2006, respectively. She is currently pursuing her Ph.D. degree in the Department of Chemical and Biological Engineering at Illinois Institute of Technology. She is a member of Process Modeling, Monitoring, and Control Research Laboratory supervised by Dr. Ali Cinar. Ms. Oruklu’s current research interests include development of subject-specific glucose prediction models, early hypoglycemic alarms, and a fully automated closed-loop glucose regulation algorithm for patients with type 1 diabetes.

graphic file with name nihms389282b2.gif

Ali Cinar is a professor of chemical engineering at Illinois Institute of Technology, Vice Provost for Research and Dean of the Graduate College at IIT since 2000 and the director of the Engineering Center for Diabetes Research and Education since 2004. His research specializations include agent-based techniques for modeling, supervision and control of complex and distributed systems, modeling of diabetes, angiogenesis and tissue formation, and automatic control of insulin pumps for patients with diabetes. Dr. Cinar holds a Ph.D. in chemical engineering from Texas A&M University. He is a member of IEEE and fellow of AIChE. He has published two books, over 180 technical papers in refereed journals and conference proceedings. Full list of publications, detailed description of research interests, presentations, and software is available at www.chbe.iit.edu/~cinar.

graphic file with name nihms389282b3.gif

Derrick K. Rollins, Sr. completed graduate degrees in Statistics (MS) and Chemical Engineering (MS and Ph.D) at The Ohio State University. His research focuses on applying statistics in chemical engineering problem solving that can benefit from stochastic modeling, including areas of biochemical engineering, biomedical engineering, system identification and process control. He has more than 60 publications spanning a variety of journals in these areas of application.

graphic file with name nihms389282b4.gif

Laurie Quinn is a Clinical Associate Professor at the University of Illinois at Chicago, College of Nursing. Dr. Quinn is experienced in the clinical management of patients with diabetes mellitus and has investigated the physiological mechanisms that contribute to their excessive rate of cardiovascular disease. Specifically, she has studied the effects of aerobic exercise on the metabolic determinants of cardiovascular disease in patients with type 2 diabetes (i.e., insulin resistance, oxidative stress, lipid and lipoprotein abnormalities). A major focus of her work has been examining the influence of aerobic exercise on postprandial metabolism in obese non-diabetic and diabetic patients. This work has led to her collaboration with Dr. Cinar and Meriyan Oruklu. Together they are investigating the temporal relationship between physical activity and glycemia using continuous glucose monitoring with the goal of integrating the information into insulin pumps.

Footnotes

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

Contributor Information

Meriyan Eren-Oruklu, Email: erenmer@iit.edu.

Derrick K. Rollins, Email: drollins@iastate.edu.

Lauretta Quinn, Email: lquinn1@uic.edu.

References

Bellazzi R, Magni P, De Nicolao G. Bayesian analysis of blood glucose time series from diabetes home monitoring. IEEE Transactions on Biomedical Engineering. 2000;47(7):971–975. doi: 10.1109/10.846693. [DOI] [PubMed] [Google Scholar]
Bode B, Gross K, Rikalo N, Schwartz S, Wahl T, Page C, Gross T, Mastrototaro J. Alarms based on real-time sensor glucose values alert patients to hypo- and hyperglycemia: the guardian continuous monitoring system. Diabetes Technology & Therapeutics. 2004;6:105–113. doi: 10.1089/152091504773731285. [DOI] [PubMed] [Google Scholar]
Buckingham B, Cobry E, Clinton P, Gage V, Caswell K, Kunselman B, Cameron F, Chase HP. Preventing hypoglycemia using predictive alarm algorithms and insulin pump suspension. Diabetes Technology & Therapeutics. 2009;11:93–97. doi: 10.1089/dia.2008.0032. [DOI] [PMC free article] [PubMed] [Google Scholar]
Derouich M, Boutayeb A. The effect of physical exercise on the dynamics of glucose and insulin. Journal of Biomechanics. 2002;35:911–917. doi: 10.1016/s0021-9290(02)00055-6. [DOI] [PubMed] [Google Scholar]
DirecNet, The Diabetes Research in Children Network Study Group. GlucoWatch G2 Biographer (GW2B) alarm reliability during hypoglycemia in children. Diabetes Technology & Therapeutics. 2004;6(5):559–566. doi: 10.1089/dia.2004.6.559. [DOI] [PMC free article] [PubMed] [Google Scholar]
Eren-Oruklu M, Cinar A, Quinn L. Hypoglycemia prediction with subject-specific recursive time-series models. Journal of Diabetes Science and Technology. 2010;4(1):25–33. doi: 10.1177/193229681000400104. [DOI] [PMC free article] [PubMed] [Google Scholar]
Eren-Oruklu M, Cinar A, Quinn L, Smith D. Estimation of future glucose concentrations with subject-specific recursive linear models. Diabetes Technology & Therapeutics. 2009a;11(4):243–253. doi: 10.1089/dia.2008.0065. [DOI] [PMC free article] [PubMed] [Google Scholar]
Eren-Oruklu M, Cinar A, Quinn L, Smith D. Adaptive control strategy for regulation of blood glucose levels in patients with type 1 diabetes. Journal of Process Control. 2009b;19(8):1333–1346. [Google Scholar]
Finan DA, Zisser H, Jovanovic L, Bevier WC, Seborg DE. Identification of linear dynamic models for type 1 diabetes: a simulation study. Proceedings of the IFAC AD-CHEM Symposium; Gramado, Brazil. 2006. [Google Scholar]
Florian JA, Parker RS. Empirical modeling for glucose control in diabetes and critical care. European Journal of Control. 2005;11:344–350. [Google Scholar]
Haykin S. Adaptive Filter Theory. 3. Upper Saddle River, NJ: Prentice Hall; 1996. [Google Scholar]
Hovorka R, Canonico V, Chassin LJ, Haueter U, Massi-Beneditti M, Federici MO, Pieber TR, Schaller HC, Schaupp L, Vering T, Wilinska ME. Nonlinear model predictive control of glucose concentration in subjects with type 1 diabetes. Physiol Measurement. 2004;25:905–920. doi: 10.1088/0967-3334/25/4/010. [DOI] [PubMed] [Google Scholar]
Katayama T, Sato T, Minato K. A blood glucose prediction system by chaos approach. Proc. of the 26th Annual International Conference of the IEEE EMBS; 2004. pp. 750–753. [DOI] [PubMed] [Google Scholar]
Kim J, Saidel GM, Cabrera ME. Multi-scale computational model of fuel homeostasis during exercise: effect of hormonal control. Annals Biomedical Eng. 2007;35:69–90. doi: 10.1007/s10439-006-9201-x. [DOI] [PubMed] [Google Scholar]
Knobbe EJ, Buckingham B. The extended Kalman filter for continuous glucose monitoring. Diabetes Technology & Therapeutics. 2005;7(1):15–27. doi: 10.1089/dia.2005.7.15. [DOI] [PubMed] [Google Scholar]
Leung SH, So CF. Gradient-based variable forgetting factor RLS algorithm in time-varying environments. IEEE Transactions on Signal Processing. 2005;53(8):3141–3150. [Google Scholar]
Mougiakakou SG, Nikita KS. A neural network approach for insulin regime and dose adjustment in type 1 diabetes. Diabetes Technology & Therapeutics. 2000;2:381–389. doi: 10.1089/15209150050194251. [DOI] [PubMed] [Google Scholar]
Palerm CC, Bequette BW. Hypoglycemia detection and prediction using continuous glucose monitoring – a study on hypoglycemic clamp data. Journal of Diabetes Science and Technology. 2007;1(5):624–629. doi: 10.1177/193229680700100505. [DOI] [PMC free article] [PubMed] [Google Scholar]
Rollins DK, Bhandari N, Kleinedler J, Kotz K, Strohbehn A, Boland L, Murphy M, Andre D, Vyas N, Welk G, Franke W. Free-living inferential modeling of blood glucose level using only noninvasive inputs. Journal of Process Control. 2009;20:95–107. [Google Scholar]
Roy A. PhD thesis. Department of Chemical and Petroleum Engineering, University of Pittsburgh; PA: 2008. Dynamic Modeling 0f Free Fatty Acid, Glucose, and Insulin During Rest and Exercise in Insulin Dependent Diabetes Mellitus Patients. [Google Scholar]
Song S, Lim JS, Baek SJ, Sung KM. Gauss Newton variable forgetting factor recursive least squares for time varying parameter tracking. Electronics Letters. 2000;36(11):988–990. [Google Scholar]
Sparacino G, Zanderigo F, Corazza S, Maran A, Facchinetti A, Cobelli C. Glucose concentration can be predicted ahead in time from continuous glucose monitoring sensor time-series. IEEE Trans Biomedical Eng. 2007;54:931–937. doi: 10.1109/TBME.2006.889774. [DOI] [PubMed] [Google Scholar]
Valletta JJ, Chipperfield AJ, Byrne CD. Gaussian process modeling of blood glucose response to free-living physical activity data in people with type 1 diabetes. Proceedings of the Annual International Conference of the IEEE EMBC; Minneapolis, USA. 2009. pp. 4913–4916. [DOI] [PubMed] [Google Scholar]
Van Herpe T, Espinoza M, Pluymers P, Wouters P, De Smet F, Van Den Berghe G, De Moor B. Development of a critically ill patient input-output model. Proceedings of the IFAC Symposium on System Identification; New-castle, Australia. 2006. [Google Scholar]
Weinstein RL, Schwartz SL, Brazg RL, Bugler JR, Peyser TA, McGarraugh GV. Accuracy of the 5-day FreeStyle Navigator Continuous Glucose Monitoring System: comparison with frequent laboratory reference measurements. Diabetes Care. 2007;30(5):1125–1130. doi: 10.2337/dc06-1602. [DOI] [PubMed] [Google Scholar]
Yamaguchi M, Kaseda C, Yamazaki K. Prediction of blood glucose level of type 1 diabetics using response surface methodology and data mining. Medical & Biological Engineering & Computing. 2006;44(6):451–457. doi: 10.1007/s11517-006-0049-x. [DOI] [PubMed] [Google Scholar]
Zainuddin Z, Pauline O, Ardil C. A Neural Network Approach in Predicting the Blood Glucose Level for Diabetic Patients. International Journal of Information and Mathematical Sciences. 2009;5(1):72–79. [Google Scholar]

[R1] Bellazzi R, Magni P, De Nicolao G. Bayesian analysis of blood glucose time series from diabetes home monitoring. IEEE Transactions on Biomedical Engineering. 2000;47(7):971–975. doi: 10.1109/10.846693. [DOI] [PubMed] [Google Scholar]

[R2] Bode B, Gross K, Rikalo N, Schwartz S, Wahl T, Page C, Gross T, Mastrototaro J. Alarms based on real-time sensor glucose values alert patients to hypo- and hyperglycemia: the guardian continuous monitoring system. Diabetes Technology & Therapeutics. 2004;6:105–113. doi: 10.1089/152091504773731285. [DOI] [PubMed] [Google Scholar]

[R3] Buckingham B, Cobry E, Clinton P, Gage V, Caswell K, Kunselman B, Cameron F, Chase HP. Preventing hypoglycemia using predictive alarm algorithms and insulin pump suspension. Diabetes Technology & Therapeutics. 2009;11:93–97. doi: 10.1089/dia.2008.0032. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R4] Derouich M, Boutayeb A. The effect of physical exercise on the dynamics of glucose and insulin. Journal of Biomechanics. 2002;35:911–917. doi: 10.1016/s0021-9290(02)00055-6. [DOI] [PubMed] [Google Scholar]

[R5] DirecNet, The Diabetes Research in Children Network Study Group. GlucoWatch G2 Biographer (GW2B) alarm reliability during hypoglycemia in children. Diabetes Technology & Therapeutics. 2004;6(5):559–566. doi: 10.1089/dia.2004.6.559. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R6] Eren-Oruklu M, Cinar A, Quinn L. Hypoglycemia prediction with subject-specific recursive time-series models. Journal of Diabetes Science and Technology. 2010;4(1):25–33. doi: 10.1177/193229681000400104. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R7] Eren-Oruklu M, Cinar A, Quinn L, Smith D. Estimation of future glucose concentrations with subject-specific recursive linear models. Diabetes Technology & Therapeutics. 2009a;11(4):243–253. doi: 10.1089/dia.2008.0065. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R8] Eren-Oruklu M, Cinar A, Quinn L, Smith D. Adaptive control strategy for regulation of blood glucose levels in patients with type 1 diabetes. Journal of Process Control. 2009b;19(8):1333–1346. [Google Scholar]

[R9] Finan DA, Zisser H, Jovanovic L, Bevier WC, Seborg DE. Identification of linear dynamic models for type 1 diabetes: a simulation study. Proceedings of the IFAC AD-CHEM Symposium; Gramado, Brazil. 2006. [Google Scholar]

[R10] Florian JA, Parker RS. Empirical modeling for glucose control in diabetes and critical care. European Journal of Control. 2005;11:344–350. [Google Scholar]

[R11] Haykin S. Adaptive Filter Theory. 3. Upper Saddle River, NJ: Prentice Hall; 1996. [Google Scholar]

[R12] Hovorka R, Canonico V, Chassin LJ, Haueter U, Massi-Beneditti M, Federici MO, Pieber TR, Schaller HC, Schaupp L, Vering T, Wilinska ME. Nonlinear model predictive control of glucose concentration in subjects with type 1 diabetes. Physiol Measurement. 2004;25:905–920. doi: 10.1088/0967-3334/25/4/010. [DOI] [PubMed] [Google Scholar]

[R13] Katayama T, Sato T, Minato K. A blood glucose prediction system by chaos approach. Proc. of the 26th Annual International Conference of the IEEE EMBS; 2004. pp. 750–753. [DOI] [PubMed] [Google Scholar]

[R14] Kim J, Saidel GM, Cabrera ME. Multi-scale computational model of fuel homeostasis during exercise: effect of hormonal control. Annals Biomedical Eng. 2007;35:69–90. doi: 10.1007/s10439-006-9201-x. [DOI] [PubMed] [Google Scholar]

[R15] Knobbe EJ, Buckingham B. The extended Kalman filter for continuous glucose monitoring. Diabetes Technology & Therapeutics. 2005;7(1):15–27. doi: 10.1089/dia.2005.7.15. [DOI] [PubMed] [Google Scholar]

[R16] Leung SH, So CF. Gradient-based variable forgetting factor RLS algorithm in time-varying environments. IEEE Transactions on Signal Processing. 2005;53(8):3141–3150. [Google Scholar]

[R17] Mougiakakou SG, Nikita KS. A neural network approach for insulin regime and dose adjustment in type 1 diabetes. Diabetes Technology & Therapeutics. 2000;2:381–389. doi: 10.1089/15209150050194251. [DOI] [PubMed] [Google Scholar]

[R18] Palerm CC, Bequette BW. Hypoglycemia detection and prediction using continuous glucose monitoring – a study on hypoglycemic clamp data. Journal of Diabetes Science and Technology. 2007;1(5):624–629. doi: 10.1177/193229680700100505. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R19] Rollins DK, Bhandari N, Kleinedler J, Kotz K, Strohbehn A, Boland L, Murphy M, Andre D, Vyas N, Welk G, Franke W. Free-living inferential modeling of blood glucose level using only noninvasive inputs. Journal of Process Control. 2009;20:95–107. [Google Scholar]

[R20] Roy A. PhD thesis. Department of Chemical and Petroleum Engineering, University of Pittsburgh; PA: 2008. Dynamic Modeling 0f Free Fatty Acid, Glucose, and Insulin During Rest and Exercise in Insulin Dependent Diabetes Mellitus Patients. [Google Scholar]

[R21] Song S, Lim JS, Baek SJ, Sung KM. Gauss Newton variable forgetting factor recursive least squares for time varying parameter tracking. Electronics Letters. 2000;36(11):988–990. [Google Scholar]

[R22] Sparacino G, Zanderigo F, Corazza S, Maran A, Facchinetti A, Cobelli C. Glucose concentration can be predicted ahead in time from continuous glucose monitoring sensor time-series. IEEE Trans Biomedical Eng. 2007;54:931–937. doi: 10.1109/TBME.2006.889774. [DOI] [PubMed] [Google Scholar]

[R23] Valletta JJ, Chipperfield AJ, Byrne CD. Gaussian process modeling of blood glucose response to free-living physical activity data in people with type 1 diabetes. Proceedings of the Annual International Conference of the IEEE EMBC; Minneapolis, USA. 2009. pp. 4913–4916. [DOI] [PubMed] [Google Scholar]

[R24] Van Herpe T, Espinoza M, Pluymers P, Wouters P, De Smet F, Van Den Berghe G, De Moor B. Development of a critically ill patient input-output model. Proceedings of the IFAC Symposium on System Identification; New-castle, Australia. 2006. [Google Scholar]

[R25] Weinstein RL, Schwartz SL, Brazg RL, Bugler JR, Peyser TA, McGarraugh GV. Accuracy of the 5-day FreeStyle Navigator Continuous Glucose Monitoring System: comparison with frequent laboratory reference measurements. Diabetes Care. 2007;30(5):1125–1130. doi: 10.2337/dc06-1602. [DOI] [PubMed] [Google Scholar]

[R26] Yamaguchi M, Kaseda C, Yamazaki K. Prediction of blood glucose level of type 1 diabetics using response surface methodology and data mining. Medical & Biological Engineering & Computing. 2006;44(6):451–457. doi: 10.1007/s11517-006-0049-x. [DOI] [PubMed] [Google Scholar]

[R27] Zainuddin Z, Pauline O, Ardil C. A Neural Network Approach in Predicting the Blood Glucose Level for Diabetic Patients. International Journal of Information and Mathematical Sciences. 2009;5(1):72–79. [Google Scholar]

PERMALINK

Adaptive System Identification for Estimating Future Glucose Concentrations and Hypoglycemia Alarms

Meriyan Eren-Oruklu

Ali Cinar

Derrick K Rollins

Lauretta Quinn

Abstract

1. Introduction