Abstract
Grid cells in the entorhinal cortex appear to represent spatial location via a triangular coordinate system. Such cells, which have been identified in rats, bats, and monkeys, are believed to support a wide range of spatial behaviors. By recording neuronal activity from neurosurgical patients performing a virtual-navigation task we identified cells exhibiting grid-like spiking patterns in the human brain, suggesting that humans and simpler animals rely on homologous spatial-coding schemes.
The hippocampal formation, which includes the hippocampus and entorhinal cortex (EC), contains a diverse array of cell types that support spatial navigation and memory. A key component of this system is the hippocampal place cell [1, 2], which encodes the animal’s presence at a particular spatial location to support navigation and encoding of spatial memories. Place cells have been identified in various species, including rats [1], mice [3], bats [4], and humans [2]. Much research has focused on how place-cell representations are formed [5] and how place cells represent the current location without the animal receiving sensory input [6]. The discovery of EC grid and grid-by-direction cells [7–9] offers a possible answer to these questions by providing the hippocampus with a robust location signal that is encoded using characteristic triangular coordinates and updated with the animal’s movements [10].
In humans, functional magnetic resonance imaging (fMRI) provides indirect support for the existence of grid cells. Recordings of fMRI activity while participants performed a spatial object-placement task revealed that hemodynamic activity in a network of regions, including EC, is modulated by the direction of movement [11]. Specifically, this direction-sensitive activity exhibits six-fold rotational symmetry, which conforms to the 60° periodicity of the spatial-firing patterns observed from recordings of grid cells in rodents [7]. Here we used invasive brain recordings to look for electrophysiological evidence of human grid cells. This would provide the first direct evidence of grid-like representations in navigating primates (humans or monkeys), thus supporting noninvasive fMRI data [11] and integrative models of spatial navigation and memory [12, 13].
To directly identify human neurons exhibiting grid-like spatial firing, we recorded single-neuron spiking activity from electrodes surgically implanted in fourteen patients undergoing treatment for drug-resistant epilepsy. Due to the clinical recording equipment used for epilepsy monitoring, patients were constrained to their bed and unable to perform a physical navigation task. Instead, patients performed a virtual navigation task on a bedside laptop computer [14]. The task required that they navigate between four objects that were hidden at different locations in a virtual environment (Fig. 1A). Unlike some previous studies of neuronal activity in human spatial navigation [2, 15], this environment was a large open square, analogous to the sizable arenas often used to record grid cells from rodents [7]. On each trial of the task the patient navigated to the location of a randomly selected object. Because objects were invisible, the patients were likely to use an allocentric navigation strategy based on path integration, which relies on the hippocampal formation [12]. Behaviorally, patients were successful in learning the locations of the four objects, as there was a significant decrease in their mean delivery time from 14 s to 8 s over the course of each session (Fig. 1B; p<0.005, t test).
Figure 1. Virtual navigation task.
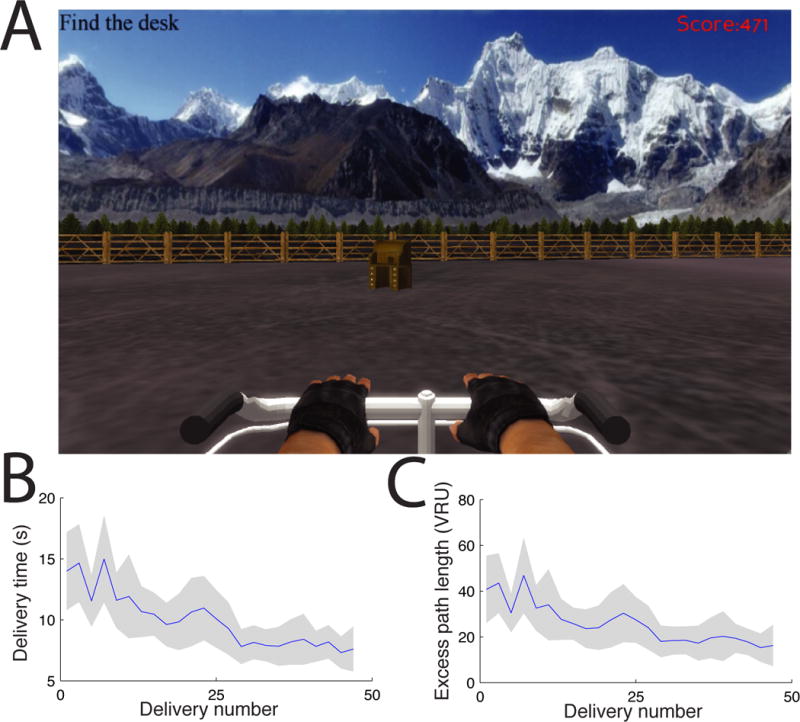
A. Patient’s view of the experiment. B. Mean duration of successive deliveries in the task, averaged across consecutive pairs of deliveries. Error bars denote 95% confidence intervals. C. Mean excess path length.
Our data analyses identified grid-like spatial firing by measuring the firing rate of each cell across the virtual environment and testing whether the locations where individual cells activated were arranged in a six-fold–symmetric triangular grid. We measured neuronal firing according to the participant’s location by dividing the square environment into a 28 × 28 array and computing the mean firing rate of each neuron for every virtual position. A number of cells exhibited increased spiking activity at multiple locations. Thus, these cells appeared to be fundamentally different from hippocampal place cells, which usually activate only at one location [5].
Next, we tested whether the multiple locations where each neuron activated were arranged in the triangular lattice structure that is characteristic of grid cells [7]. This allows us to distinguish cells with grid-like firing from other cells that activate at multiple spatial locations, such as multipeaked place cells [5]. To measure the spatial arrangement between the locations represented by each cell’s firing, we computed the two-dimensional spatial autocorrelation function for each cell’s firing rate map. We found that the autocorrelation functions of many cells exhibited multiple distinct peaks that were arranged symmetrically (Fig. 2, middle panels). In many cases these patterns exhibited six-fold (60°) symmetry, which indicated that the locations where these cells activated were arranged in a triangular grid, similar to patterns observed in rodents [7, 10].
Figure 2. Examples of grid-like spatial firing.
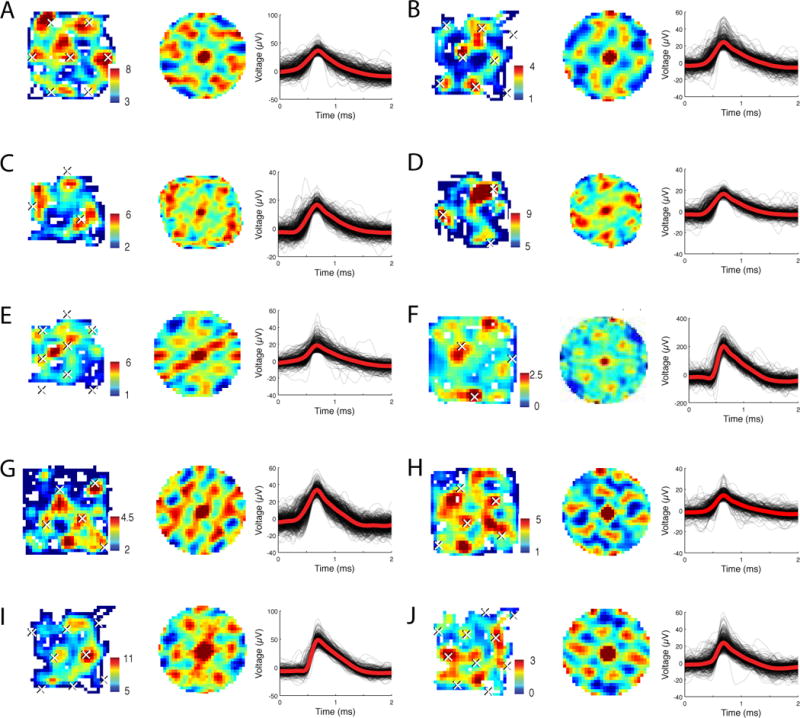
A. The activity of a cell from Patient 6’s left entorhinal cortex (EC). The left panel shows an overhead view of the environment, with color representing the firing rate (in Hz) at each virtual location (See also Fig. S6). The middle panel depicts the 2-D autocorrelation of the cell’s activity. Peaks in the autocorrelation function determine the spacing and angle of the fitted grid, which is then used to plot the estimated grid peaks as white ×s across the entire environment. Right panel shows the cell’s spike waveform. This cell had a gridness score of 0.51. B. The firing of a different cell from Patient 10’s right EC (gridness score 0.63). C & D. The firing of a cell from Patient 10’s right EC in two consecutive sessions (gridness scores 0.6 and 0.74, respectively). E. The activity of a different cell from Patient 10’s right EC (gridness score 0.63). F. The activity of a cell from Patient 11’s right cingulate cortex (CC) (gridness score 0.67). G. The activity of a cell from Patient 7’s right CC (gridness score 0.51). H. The activity of a cell from Patient 7’s right CC (gridness score 0.8). I. The activity of a cell from Patient 10’s right hippocampus (gridness score 0.46). J. The activity of a cell from Patient 10’s right parahippocampal gyrus (gridness score 0.72).
To identify cells with significant grid-like spatial firing, we computed each cell’s gridness score, which quantifies the 60° periodicity in the cell’s spatial autocorrelation function [7]. The gridness score is computed as the mean difference in the autocorrelation at the angles where peaks would be expected in true grid cells (60° and 120°) compared with the angles where troughs would be expected (30°, 90°, and 150°). A neuron was designated as exhibiting grid-like spatial firing if its gridness score was significantly greater than expected by chance (p<0.05; see Methods and Fig. S2).
We applied this grid identification procedure to each of the 893 cells in our dataset, including cells from EC, hippocampus, amygdala, parahippocampal gyrus, and cingulate cortex (Fig. 3A). Many cells exhibited significant grid-like activity. These cells were not uniformly distributed across brain areas (p<0.001, test). The most grid-like cells were found in the EC and cingulate cortex, which contained 14% and 12% grid cells, respectively (p’s<0.0005, binomial tests; Fig. 3B). This peak proportion of grid-like cells in the entorhinal cortex is generally consistent with findings from previous human and animal studies [7, 9, 11]. There were also significant levels of grid-like cells in the hippocampus (8%, p=0.05). There was no significant difference in the prevalence of grid-like cells between the right and left hemispheres (p>0.5, test).
Figure 3. Population measurements of cells exhibiting significant grid-like spatial firing.
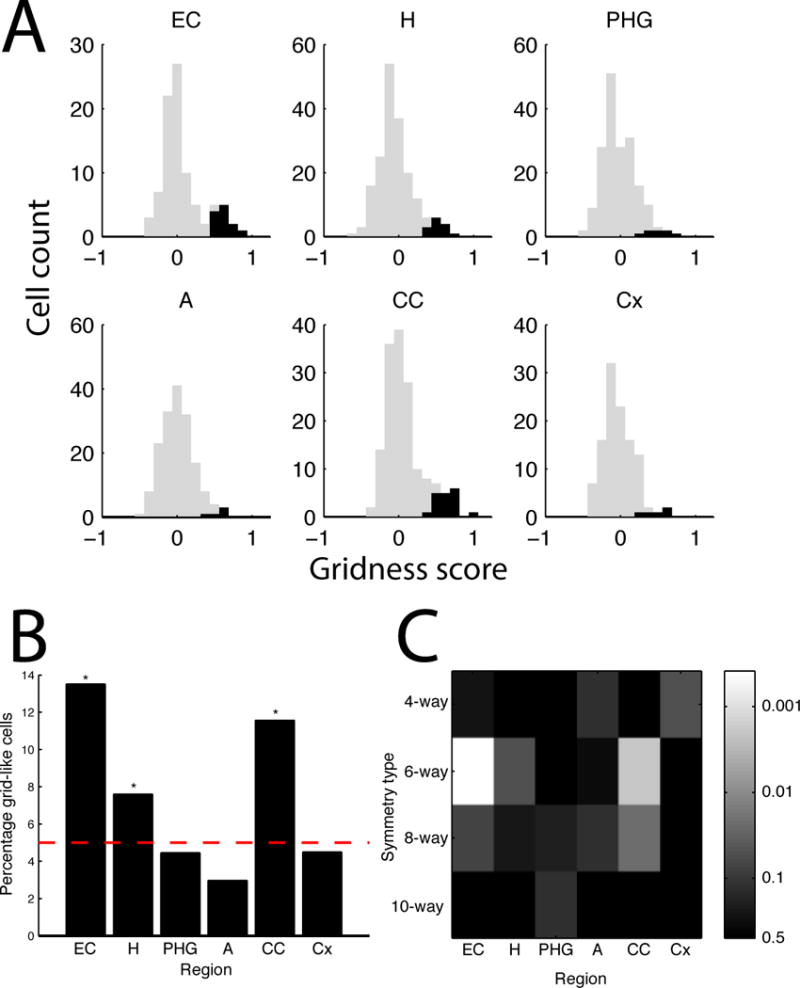
A. The distribution of gridness scores from each region. Black bars indicate the gridness scores of cells that exhibited significant grid-like activity (p<0.05), gray bars indicate other cells. Region labels: EC, entorhinal cortex; H, hippocampus; PHG, parahippocampal gyrus; A, amygdala; CC, cingulate cortex; Cx, frontal cortex. B. The proportion of significant grid-like cells across regions. Dotted line indicates the Type 1 error rate (5%). Asterisks denote regions where the observed number of cells exceeds the Type 1 error rate at p<0.01 (binomial test). C. The significance of cells exhibiting 4-, 6-, 8-, and 10-fold symmetric activity (binomial test).
To verify that the six-fold rotational symmetry of grid-like cells is a distinctive feature of human neuronal coding, we tested for cells whose spatial firing exhibited 4-, 8- or 10-fold rotational symmetry. The 8- and 10-fold symmetry analyses served as statistical control analyses, as grids with these angles do not tesselate. These analyses did not reveal significant levels of cell exhibiting 4-, 8-, or 10-way symmetric activity (Fig. 3C). Thus, the only significant symmetric spatial firing pattern in the data was the 6-fold symmetry associated with grid cells. In particular, because we did not observe significant 4-way rotational symmetry, we ruled out the possibility that the firing patterns could be driven by the square-like arrangement of the four objects.
Prior studies revealed detailed features of grid cells related to the spacing and direction-sensitivity of their representations [7, 10, 11]. Technical reasons precluded us from examining the relation between grid spacing and anatomical location of the recording electrode within the EC [7, 9]. Comparing anterior and posterior cingulate, we found similar levels of grid-like cells in each area (12% and 11%, respectively) and observed a trend whereby cells in anterior cingulate had more widely spaced grids than cells in posterior cingulate (p=0.1). Of the cells exhibiting grid-like spatial firing, 18% exhibited an additional direction-related modulation (Table S3), which is consistent with them exhibiting conjunctive grid-by-direction responses [10]. We found similar levels of grid-like spatial responses after statistically removing direction-related spiking activity, which indicates our main findings of grid-like patterns were not artifacts of neural responses to direction or turning. We also conducted additional control analyses to confirm that the grid-like cells we observed were stable over time (Fig. S5) and not the result of multi-peaked place cells (Fig. S2).
In rodents, grid cells are part of a broader neuronal network related to spatial processing including hippocampal place cells, which represent the animal’s presence at individual locations [1, 2]. We identified place cells by identifying cells that had significantly elevated firing when the patient was at a specific virtual location (the cell’s place field; Fig. S1A–D). We observed significant levels of place cells in the hippocampus, parahippocampal gyrus, and cingulate cortex (p’s<0.01; Fig. S1E). Consistent with recordings in animals navigating open environments, 80% of place cells did not significantly vary their firing rate in the place field according to the patient’s heading—the remaining 20% of place cells were direction-sensitive. We also tested for cells whose activity increased when the person faced a particular virtual direction without necessarily encoding specific locations. Significant levels of direction-sensitive cells were found only in the hippocampus and parahippocampal gyrus (7% of cells in each region; p’s<0.03, binomial tests). Owing to the open environment in our task, the patient’s direction correlates with viewing particular landmarks at the arena’s boundaries. Thus, some apparent direction-sensitive cells may relate to viewing particular landmarks [2, 16]. Finally, we tested for cells that represent combinations of linear regions of the environment [17] but the results were inconclusive.
Our results demonstrate the existence of cells with grid-like spatial firing in the human brain and suggest that the human grid-cell network includes EC as well as cingulate cortex. These results extend to humans an important growing body of research in rodents [7, 10] and support the general finding of Doeller et al. [11] from fMRI that there are grid-like patterns in the human EC as well as in the frontal lobe (note that the cingulate cortex where we found grid-like cells is posterior to the prefrontal areas reported by Doeller et al.) Although it is difficult to extrapolate accurately from virtual to real-world movement, our estimate of the patient’s perceived walking speed (~1.25–2 m/s, computed from the optic flow and their viewpoint height), suggests that individual grid cell firing fields have spacings between firing fields of at least ~1–6 meters in the physical world (extrapolating from the observed virtual grid spacings that spanned 27–84% of the environment’s width; see white ×’s in Fig. 2).
Although statistically robust, the grid-like cells we observed have noisier firing maps than some grid cells reported in rodents. Whereas scientists studying rodent grid cells generally _target the dorsomedial EC precisely, there is localization variability in epilepsy patients because neurosurgeons implant electrodes according to clinical needs [14]. It is also important to understand whether the activities of human grid-like cells are affected by other factors besides location, such as eye position, which was shown to modulate grid cells in monkeys [9]. An additional factor is that humans perform our virtual navigation task using only visual information and thus do not receive the proprioceptive feedback that occurs during normal locomotion and was shown to be important for accurate spatial representations in rodents [18].
By demonstrating the presence of human grid-like representations during spatial navigation and learning, our findings suggest that grid cells play an important role in human cognition [13]. Given the purported role of the EC in spatial and non-spatial behaviors [13, 19], it seems likely that analogous grid-like signals also represent various types of human behavioral information. Thus, one important area of future research is characterizing the information coding of these cells during non-navigational behaviors and, furthermore, characterizing relations between grid cells, head-direction cells, and eye movements [9]. The EC is the main input to the hippocampus, which is critical for episodic memory. Obtaining a better understanding of the behavior of widespread EC cells [7, 17, 19, 20] is likely to shed light on how the human brain encodes spatial and non-spatial episodic memories in various contexts.
Online Methods
Task
During free time between clinical procedures, patients performed a spatial learning task on a bedside laptop computer. Our testing protocol is approved by the institutional review boards of Thomas Jefferson University and the University of California, Los Angeles. In this task, patients learned the locations of four visible goal objects and then re-navigated to these locations with the objects invisible. At the beginning of each session, each of the four objects were shown sequentially on a black screen for 2000 ms to familiarize the participants with their appearance; this repeated five times. Participants were then placed in the virtual environment where they began navigating, using a joystick to control the direction of their movement. In each trial the participant was instructed to drive a virtual bicycle to the location of a randomly selected object. The virtual environment consisted of a large open square arena with visual cues that included textured walls, a panoramic background image, and a floor that gradually transitioned between different colors. The patient’s top speed of movement allowed them to travel between opposite walls of the environment in ~3.5 seconds. We defined the width of the environment as 28 VRU.
The beginning of each session was a training period to teach the patient the objects’ locations. Each training trial began with the patient in the middle of the environment facing a single wall (“north”). Then they twice navigated to each object: the first time the object was clearly visible, and the second time, after being transported back to the center of the environment, the object was invisible until they were within 1.6 VRU. The patients visited each of the four objects in a random order, and then repeated this process three times for a total of twelve training trials. The objects were positioned in a large square-like shape (minor variations across sessions) to encourage patients to navigate throughout the environment.
After training, participants performed 48 delivery trials where they were asked to navigate directly from one object location to another. The goal object remained invisible until the participant was very close to its location. In rare cases when participants became disoriented, the experimenter could intervene to manually make the goal object appear. Participants navigated to each fixed goal location 12 times in a random order; there were approximately equal numbers of navigations between each pair of objects. We excluded seven sessions where patients had poor navigation performance (defined as having an mean excess delivery path length greater than 100 VRU).
Electrophysiology
We recorded single-neuron spiking from 40-μm research microwires that augmented the standard clinical macroelectrodes used by clinical teams to map epileptiform activity. Nine patients were recorded by I.F. using customized microelectrodes that extended from the tip of clinical depth electrodes. Five patients were recorded by A.S. using electrodes from AdTech Corporation that had microwires positioned on either the side or tip of each depth electrode. We localized electrodes by performing computed tomography (CT) scans after implant, aligning the CT images with pre-implant MRIs (Fig. S4), and then labeling the region of each electrode according to anatomical landmarks We recorded electrical activity at 28–32 kHz and identified spikes from individual cells using wavelet clustering and temporal autocorrelations [21]. The amplitude of individual spike waveforms averaged 48 μV (see Table S2). Our accuracy in distinguishing individual cells and background noise is largely consistent with recordings from animals, as measured using standard methods [22]: 76% of cells had a false-negative error rate less than 10% and 82% had an error rate less than 20%. 78% of cells had a false-positive error rate less than 10% and 85% had an error rate less than 20%.
Data analysis
Our data analyses probed the relation between each cell’s firing rate and the participant’s location in the virtual environment. We excluded cells with mean firing rates below 0.5 Hz or above 9 Hz (potential interneurons). We divided each recording session into 50-ms epochs and excluded any time intervals when the participant was not moving. Then, we computed the firing rate of each neuron across the environment, binning this activity into a 28 × 28 array and excluding any locations that were not occupied for at least 100 ms (~24% of the environment excluded on average). This firing-rate map was then smoothed with a 5×5 gaussian kernel [7].
To characterize the spatial firing of each neuron we computed the spatial autocorrelation, r, of each neuron’s smoothed firing rate [7]. This function identifies spatial patterns in the cell’s firing by computing the correlation between the firing rates at positions (x,y) and , aggregating across all locations (x,y) in the environment:
where and correspond to spatial lags, λ(x,y) is the firing rate at array location (x,y), n corresponds to the number of valid observations for (x,y), . To minimize potential spurious patterns, we only computed for values with at least 20 observations.
Using this autocorrelation function, we then computed each neuron’s gridness score [10] as the correlation (cor) between the elements in the original autocorrelation matrix r and a series of rotated autocorrelation matrices where is the angle of rotation. Each cell’s gridness score, g, was thus determined as
To identify the spacing of each grid cell, we computed each cell’s maximum gridness score across radii L∈5…28, in each computation including only such that .
We used a permutation procedure to identify putative grid cells by comparing each cell’s observed gridness score, g, with the distribution of gridness scores expected by chance for that cell, g*. To estimate g* for each cell, we reshuffled the original spiking data 1000 times and, for each shuffle, computed the gridness scores exactly as described above. This reshuffling preserved the temporal correlations in the patient’s behavior and neural activity by randomly rotating the spiking data with a circular wraparound. We designated a neuron as a putative grid cell if its true gridness score exceeded 95% of the distribution of g* and was positive. To identify cells exhibiting 4-, 8-, or 10-fold symmetric firing (Fig. 3C), we followed an analogous procedure but instead used appropriate angles when computing g (e.g., for 4-fold symmetry, we used .
To identify place cells, we used t tests to compare the firing rate within 5 VRUs of each virtual location with the activity at other locations [15]. A neuron was designated as a place cell if its smallest location-related p value was less than observed from reshuffled data at p<0.05. This procedure used the time-shifting reshuffling described above and thus it was unlikely for significant place cells to be caused by only a single traversal of a given location. We identified direction-sensitive place cells by using an ANOVA to determine if the cell’s firing inside the place field significantly varied according to the cardinal direction the patient faced.
Supplementary Material
Acknowledgments
We are grateful to the patients for participating in our study. This work was supported by NIH grants MH061975 and NS033221. We thank Kenton Lee, Dale Wyeth, Edmund Wyeth, Deena Pourshaban, Eric Behnke, and Tony Fields for technical assistance.
Footnotes
Contributions
The experiment was designed by J.J., C.T.W., M.J.K., A.S., and I.F. J.J., C.T.W., J.F.M., J.B., I.F., M.S., A.D.S., and N.S. collected the data. Data analyses were performed by J.J., X.W., C.T.W., A.S., and M.J.K. J.J. and M.J.K. wrote the manuscript.
Contributor Information
Joshua Jacobs, Email: joshua.jacobs@drexel.edu.
Itzhak Fried, Email: ifried@mednet.ucla.edu.
Michael J. Kahana, Email: kahana@psych.upenn.edu.
References
- 1.O’Keefe J, Dostrovsky J. Brain Research. 1971;34:171–175. doi: 10.1016/0006-8993(71)90358-1. [DOI] [PubMed] [Google Scholar]
- 2.Ekstrom AD, et al. Nature. 2003;425:184–187. doi: 10.1038/nature01964. [DOI] [PubMed] [Google Scholar]
- 3.McHugh T, et al. Cell. 1996;87:1339–1349. doi: 10.1016/s0092-8674(00)81828-0. [DOI] [PubMed] [Google Scholar]
- 4.Ulanovsky N, Moss C. Nature. 2007:224–233. doi: 10.1038/nn1829. [DOI] [PubMed] [Google Scholar]
- 5.Muller RU, et al. Journal of Neuroscience. 1987;7:1935–1950. doi: 10.1523/JNEUROSCI.07-07-01935.1987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Quirk G, et al. Journal of Neuroscience. 1990;10:2008–2017. doi: 10.1523/JNEUROSCI.10-06-02008.1990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Hafting T, et al. Nature. 2005;436:801–806. doi: 10.1038/nature03721. [DOI] [PubMed] [Google Scholar]
- 8.Yartsev M, et al. Nature. 2011;479:103–107. doi: 10.1038/nature10583. [DOI] [PubMed] [Google Scholar]
- 9.Killian N, et al. Nature. 2012;491:761–764. doi: 10.1038/nature11587. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Sargolini F, et al. Science. 2006;312:758–762. doi: 10.1126/science.1125572. [DOI] [PubMed] [Google Scholar]
- 11.Doeller CF, Barry C, Burgess N. Nature. 2010;463:657–661. doi: 10.1038/nature08704. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Bird C, Burgess N. Nature Reviews Neuroscience. 2008;9:182–194. doi: 10.1038/nrn2335. [DOI] [PubMed] [Google Scholar]
- 13.Buzsáki G, Moser E. Nature Neuroscience. 2013;16:130–138. doi: 10.1038/nn.3304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Jacobs J, Kahana MJ. Trends in Cognitive Sciences. 2010;14:162–171. doi: 10.1016/j.tics.2010.01.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Jacobs J, et al. Proceedings of the National Academy of Sciences, USA. 2010;107:6487–6482. [Google Scholar]
- 16.Rolls E. Hippocampus. 1999;9:467–480. doi: 10.1002/(SICI)1098-1063(1999)9:4<467::AID-HIPO13>3.0.CO;2-F. [DOI] [PubMed] [Google Scholar]
- 17.Krupic J, Burgess N, O’Keefe J. Science. 2012;337:853–857. doi: 10.1126/science.1222403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Terrazas A, et al. The Journal of Neuroscience. 2005;25:8085–8096. doi: 10.1523/JNEUROSCI.0693-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Hargreaves E, et al. Science. 2005;308:1792–1794. doi: 10.1126/science.1110449. [DOI] [PubMed] [Google Scholar]
- 20.Tsao A, et al. Current Biology. 2013;23:399–405. doi: 10.1016/j.cub.2013.01.036. [DOI] [PubMed] [Google Scholar]
- 21.Quiroga R, et al. Neural Computation. 2004;16:1661–1687. doi: 10.1162/089976604774201631. [DOI] [PubMed] [Google Scholar]
- 22.Hill D, Mehta S, Kleinfeld D. The Journal of Neuroscience. 2011;31:8699–8705. doi: 10.1523/JNEUROSCI.0971-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


