In human physiology research, response variance is often anticipated and addressed in sample size planning. This planned approach is intended to provide due consideration of variation when seeking to detect a _targeted net mean effect with reasonable precision. Although this form of planning often results in dichotomous findings (i.e., significant, non-significant), rarely do “non-significant” findings completely rule out meaningful effects. Given current recommendations by many journals to present individual data and increasing initiatives on precision health (Booth & Laye, 2010; Atkinson & Batterham, 2015; Ross et al., 2019), researchers are increasingly interested in differences in response variance, in addition to the net mean treatment effect. This form of secondary analysis may involve identifying variables that predict responders (individuals for which an intervention is beneficial) vs. non-responders (those for which an intervention has no benefit). As elegantly articulated by Islam and Gurd in their recently published article entitled, “Random error or true differences in exercise response?” (Islam & Gurd, 2020), an important consideration here is whether such heterogeneity in response to an intervention is attributed to (i) a differential, but inherent, physiological response (one that is reproducible) among individuals, or (ii) the influence of random error (i.e., noise due to technical and/or biological sources). In such instances, close attention should also be placed on the statistical approach employed for such secondary analysis, as elaborated below.
Where things go wrong
As noted above, experimental protocols which pre-specify an interest in response variance between intervention and control are well-prepared to explore this idea of treatment response heterogeneity (i.e., “responders” and “non-responders”). A secondary analysis that is inappropriate, but unfortunately commonly encountered in the literature, entails determining whether the individuals with low levels of outcome variable Y prior to the intervention (e.g., participants with impaired vascular function) are the individuals that have the greatest change in outcome variable Y following treatment X (e.g., exercise training). If each individual receives treatment X, this form of post-hoc analysis will likely produce the postulated finding – but not owing to a biological effect. Examining group differences in outcome variable Y when groups are categorized/divided by outcome variable Y violates the assumption of statistical independence and essentially ensures group differences will be observed (regression to the mean). Accordingly, this secondary analysis (dividing groups by the outcome being tested) can lead to serious misinterpretation of the data.
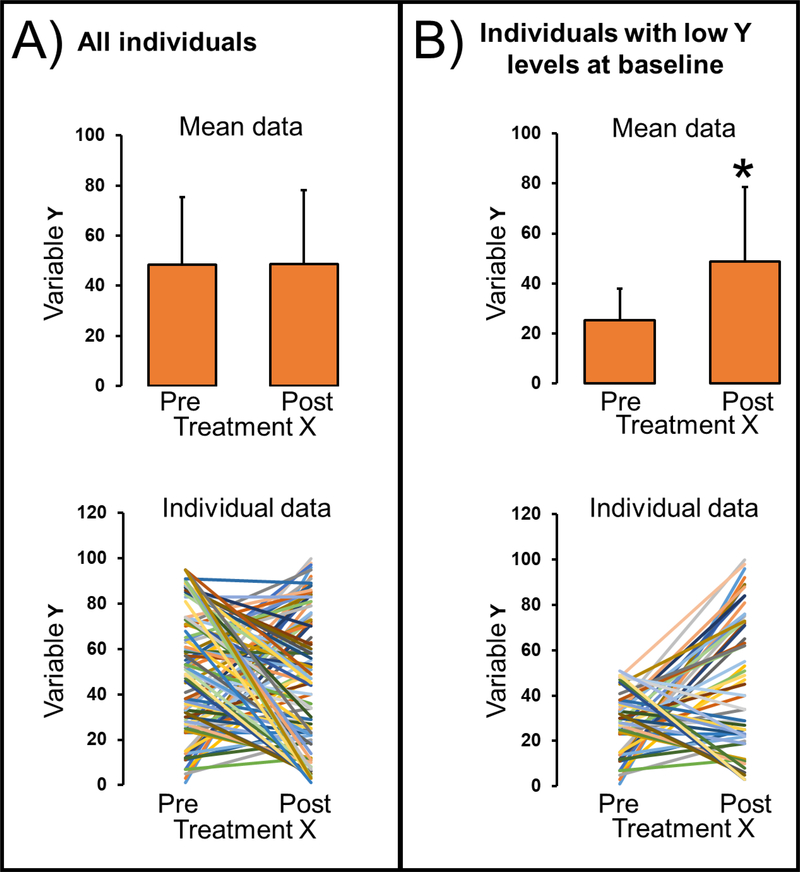
Presented in Figure 1, we walk the reader through the above scenario using randomly-generated normally distributed data for 100 individuals. In this example, values between 0 and 100 were randomly generated for outcome variable Y prior to and following treatment X using the Excel function [=RANDBETWEEN(0,100)]. In keeping with the supposition that treatment X is exercise training and outcome variable Y is vascular function, one would observe no effect of exercise training on vascular function (panel A). A secondary analysis involving the selection of individuals based on low baseline levels of vascular function would lead to an erroneous conclusion that those with impaired vascular function at baseline are more likely to exhibit an increase following exercise training (panel B). Conceptually, this makes sense as it is consistent with the notion that individuals that benefit from exercise are those that exhibit greater room for improvement. However, this analysis is statistically inappropriate as the outcome of vascular function is not independent from how individuals were grouped (e.g., low levels of vascular function prior to the intervention) and thus violates a fundamental assumption to test group differences.
Figure 1. A randomly-generated dataset illustrating a statistically inappropriate secondary analysis that is commonly encountered in the literature.
Panel A includes mean (top) and individual (bottom) data for all individuals (n=100). No significant differences in variable Y in response to treatment X were noted by paired t-test (p=0.92). Panel B includes mean (top) and individual (bottom) data for individuals with lowest Y levels at baseline (n=50). A significant effect of treatment X was noted by paired t-test (p<0.01). Error bars in top sub-panels denote standard deviation. Data were randomly generating using the Excel function [=RANDBETWEEN(0,100)]. The analysis presented in panel B lead to the erroneous conclusion that treatment X increases Y in individuals with low levels of Y at baseline.
The Solution
For a secondary analysis of this nature to be valid, the implementation of a control condition is required. The control condition should be built into the experimental design, such as in a crossover design or by including a separate cohort of control participants. The control condition allows one to discern what portion of the change in outcome variable Y in response to treatment X is actually attributable to the effect of X and not to chance or baseline values of Y. To test if baseline values of outcome variable Y are associated with the effect of treatment X, a treatment-by-baseline interaction term is required.
Impact and Future
Inadvertently, the current literature is flooded with analyses that lack appropriate control conditions, potentially leading to incorrect conclusions. We hope this commentary, along with the original article by Islam and Gurd (Islam & Gurd, 2020), serves to increase awareness of the influence of random error and the importance of incorporating control conditions for proper data interpretation, particularly in the setting of secondary analyses focused on identifying responders vs. non-responders. Rigorous training in statistics and research methods, whether in the classroom, at conferences, or more informally through journal club discussions, should continue to be promoted among physiologists.
Take Home Message:
Consideration of control conditions is critical to experimental design, needed for sound statistical inference, and will aid in post-hoc analyses to reach statistically appropriate conclusions. Robust analytical methods are crucial, but research design should be the priority. Indeed, no amount of statistical sophistication can compensate for a weak study design.
Acknowledgments
Funding
J.P. is supported by the National Institutes of Health (NIH) NIH R01 HL137769, E.L. is supported by NIH R34 AR074209A and Department of Defense research grant, J.K.L is supported by the NIH R00 HL130339 and R01 HL153523.
Footnotes
Disclosures
No conflicts of interest, financial or otherwise, are declared by the authors.
References
- Atkinson G & Batterham AM (2015). True and false interindividual differences in the physiological response to an intervention. Exp Physiol 100, 577–588. [DOI] [PubMed] [Google Scholar]
- Booth FW & Laye MJ (2010). The future: genes, physical activity and health. Acta Physiol (Oxf) 199, 549–556. [DOI] [PubMed] [Google Scholar]
- Islam H & Gurd BJ (2020). Random error or true differences in exercise response? Exp Physiol in press. [DOI] [PubMed] [Google Scholar]
- Ross R, Goodpaster BH, Koch LG, Sarzynski MA, Kohrt WM, Johannsen NM, Skinner JS, Castro A, Irving BA, Noland RC, Sparks LM, Spielmann G, Day AG, Pitsch W, Hopkins WG & Bouchard C (2019). Precision exercise medicine: understanding exercise response variability. Br J Sports Med 53, 1141–1153. [DOI] [PMC free article] [PubMed] [Google Scholar]