Abstract
Subclonal architectures are prevalent across cancer types. However, the temporal evolutionary dynamics that produce tumour subclones remain unknown. Here we measure clone dynamics in human cancers using computational modelling of subclonal selection and theoretical population genetics applied to high throughput sequencing data. Our method determines the detectable subclonal architecture of tumour samples, and simultaneously measures the selective advantage and time of appearance of each subclone. We demonstrate the accuracy of our approach and the extent to which evolutionary dynamics are recorded in the genome. Application of our method to high-depth sequencing data from breast, gastric, blood, colon and lung cancers, as well as metastatic deposits, showed that detectable subclones under selection, when present, consistently emerged early during tumour growth and had a large fitness advantage (>20%). Our quantitative framework provides new insight into the evolutionary trajectories of human cancers, facilitating predictive measurements in individual tumours from widely available sequencing data.
Introduction
Carcinogenesis is the result of Darwinian selection for malignant phenotypes, driven by genetic and epigenetic alterations that allow cells to evade normal homeostatic regulation and prosper in changing microenvironments1. High throughput genomics has shown that tumours across all cancer types are highly heterogeneous2,3 with complex clonal architectures4. However, because longitudinal observation of solid tumour growth unperturbed by treatment remains impractical, the temporal evolutionary dynamics that produce subclones remain undetermined, and consequently, there is no mechanistic basis that can be utilised to predict future tumour evolution and modes of relapse. More specifically, the magnitude of the fitness advantage experienced by a new cancer subclone has remained unknown.
The subclonal architecture of a cancer – as measured by the pattern of intra-tumour genetic heterogeneity (ITH) – is a direct consequence of the unobservable evolutionary dynamics of tumour growth. Therefore, given a realistically constrained model of subclonal expansion, the pattern of ITH in a tumour can be used to infer its most probable evolutionary trajectory. ITH represented within the distribution of variant allele frequencies (VAF), as measured by high coverage sequencing, is particularly amenable to such an approach.
In this study, we build upon theoretical population genetics models of asexual evolution5 and Bayesian statistical inference on genetic data6 to measure cancer evolution in human tumours. This type of approach is established in the field of molecular evolution, where evolutionary processes are also difficult to measure directly7,8, and examples of applications of these approaches to human cancers date back to the previous century9,10.
Recently, we have shown that under a neutral “null” evolutionary model (i.e. when all selected driver alterations are truncal and present in all cancer cells), the VAF follows a characteristic power law distribution11. Subsequent simulations that modelled space and subclonal selection demonstrated that genetic divergence in multi-region sequencing data could be used to categorize tumours based on the mode of their evolution12 (effectively-neutral or non-neutral), but the specific evolutionary dynamics that produce subclonal architectures, such as the fitness advantage of subclones, remained unmeasured. Here, using a combination of a stochastic branching process model of subclonal selection in cancer, an explicit sequencing error model, and Bayesian model selection and parameter inference, we identify the characteristic patterns of subclonal selection in the cancer genome and measure fundamental evolutionary parameters in non-neutrally evolving human tumours.
Results
Theoretical framework of subclonal selection
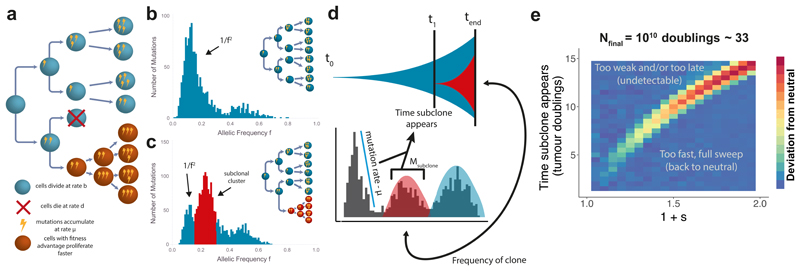
We developed a stochastic computational model of tumour growth applicable to cancer genomic data that accounts for subclonal selection (see Methods). The model is based on a classical stochastic branching process approach from population genetics13 that has been often used to model malignant populations5,14 and is here extended to be applicable to cancer sequencing data. Cells divide and die according to defined birth and death rates and daughter cells acquire new mutations at rate μ mutations per cell per division (Figure 1a). The fitness advantage of a mutant subclone is defined by the ratio of net growth rates between the fitter mutant (λm) and the background host population (λb)
| [1] |
This definition13 provides an intuitive interpretation for the fitness coefficient s: for example, s=1 implies that the mutant cell population grows twice as fast as the host tumour population, and s=0 implies λm=λb such that the subclone evolves neutrally with respect to the background population. Within the model, neutral evolution (s=0) leads to a VAF distribution characterised by a power-law distributed subclonal tail of mutations11,15–17 (Figure 1b), where the cumulative number of mutations at a frequency f is proportional to the inverse of that frequency, 1/f (in the non-cumulative VAF distribution such as Figure 1b, this shows as ~1/f2). Alternatively, clonal selection (s>0) produces characteristic ‘subclonal clusters’ within the VAF distribution that have been observed in cancer genomes18 (Figure 1c). Importantly, as neutral mutations continue to accumulate within each subclone, the 1/f tail is also present in tumours with selected subclones (Figure 1c).
Figure 1. Modelling patterns of subclonal selection in sequencing data.
(a) In a stochastic branching process model of tumour growth cells have birth rate b and death rate d, mutations accumulate with rate μ. Cells with fitness advantage (orange) grow at a faster net rate (b-d) than the host population (blue). (b) The variant allele frequency (VAF) distribution contains clonal (truncal) mutations around f=0.5 (in this example of diploid tumour), and subclonal mutations (f<0.5) which encode how a tumour has grown. In the absence of subclonal selection, a neutral 1/f2 tail describes the accumulation of passenger mutations as the tumour expands. (c) A selected subclone produces an additional peak in the distribution while a 1/f2 tail is still present due to passenger mutations accumulating in both the original population and the new subclone. (d) In the presence of subclonal selection, the magnitude and average frequency of the subclonal cluster of mutations (red) encode the age and size of a subclone respectively, which in turn allows measuring the clone’s selective advantage. (e) Frequentist power analysis of detectability of an emerging selected subclone on simulated data. Only early and/or very fit subclones caused significant alterations of the clonal composition of a tumour, resulting in the rejection of the neutral (null) model. Tumours were simulated to 106 cells and scaled to a final population size of 1010 with a mutation rate of 20 mutations per genome per division, each pixel represents the average value for the metric (area between curves) over 50 simulations.
A mathematical analysis of the model indicates how subclonal clusters encode the underlying evolutionary dynamics of a subclone: the mean VAF of the cluster is a measure of the relative size of the subclone within the tumour, and the total number of mutations in the cluster (i.e. the area of the cluster) indicates the subclone’s relative age (as later-arising subclones will have accumulated more mutations). Together, these two measures allow the fitness advantage s to be estimated19. We provide a summary derivation below and refer to the Supplementary Note for full details.
We define t0=0 to be the time when the first transformed cancer cell begins to grow. At a later time t1, a cell in the tumour acquires a subclonal ‘driver’ somatic alteration that confers a fitness advantage, giving rise to a new phenotypically distinct subclone that expands faster than the other tumour cells. We note that to measure selection dynamics it is not important what the actual driver event is: genetic (point mutation or copy number alteration), epigenetic, or even microenvironmental drivers will all cause somatic mutations in the selected lineage to ‘hitchhike’20 to higher frequencies than expected under the neutral null model. The number of hitchhiking mutations, Msub acquired by the founder cell of the fitter subclone which has experienced Γ successful divisions between t0 and t1 is therefore
| [2] |
The relationship between the mean number of divisions of a lineage, Γ and time measured in population doublings is Γ = 2log(2)t1 (see Supplementary Note). The mutation rate per population doubling can be estimated from the 1/f-like tail11. For a subclone that emerges at time t1, we would expect to observe Msub mutations at some frequency fsub/2 (for a subclone at a cancer cell fraction fsub in a diploid genome, and assuming a sample with 100% tumour purity), and given the limited accuracy of VAF measurement inherent to next generation sequencing this will appear as a cluster of mutations with a mean fsub/2 in the VAF distribution. Therefore, Equation [2] provides an estimate of t1, the time when the subclone appeared.
Assuming exponential growth and well mixed populations, and considering that the subclone grows 1+s times faster than the background tumour population as defined by Equation [1], the frequency of the subclone will grow in time according to:
| [3] |
This equation leads to an expression for the fitness advantage s given the frequency fsub and the relative time of the subclones appearance t1,
| [4] |
Given an estimate of the age of the tumour expressed in population doublings tend, equations [2] and [4] provide a means to measure the selective advantage of a subclone directly from the VAF distribution (Figure 1d). tend can be derived from the final tumour size Nend by the relation 2tend = (1 – fsub) × Nend. In the case of multiple subclones, Equation [4] takes a slightly modified form (Supplementary Note). We note that Equations [1-4] are known results in population genetics and have been previously used to describe the dynamics of asexual haploid populations 13.
Our previously presented frequentist approach to detect subclonal selection from bulk sequencing data involves an R2 test statistic19 to reject the hypothesis of neutral evolution (s=0), the null model in molecular evolution21. Here we extended our previous work to examine different test statistics for assessing deviations from the null neutral model (see Supplementary Figures 1-3 & Methods). However, the frequentist approach has limitations: it requires to choose the interval of the VAF distribution to test, and importantly only allows for the rejection of the null hypothesis (which is not necessarily evidence for the null itself).
To address these shortcomings, we implemented a Bayesian statistical inference framework (Supplementary Figure 4 & Methods) that fits our computational model incorporating both selection and neutrality to sequencing data, and simultaneously estimates the subclone fitness, time of occurrence, and the mutation rate. This method allowed us to perform Bayesian model selection22 for the number of subclones within the tumour and specifically calculate probabilities that a tumour contained 0 subclones (s=0, neutral evolution), 1 or more subclones (non-neutral evolution). The advantage of the Bayesian approach is that we can directly ask which model (neutral or non-neutral) is best supported by the data, using the whole VAF distribution.
Our framework models mutation, selection and neutral drift using a classical stochastic branching process13, while integrating several confounding factors and sources of noise in bulk sequencing data, principally allele sampling and depth of sequencing (see Methods and Supplementary Note). This approach allows sample-based schemes designed such that the data-generating process can be mimicked to account for complex experimental biases. Despite these confounding factors, we found that the 1/f tail accurately measures the mutation rate even in the presence of subclonal clusters (Supplementary Figure 5), and our inferred value of 1+s is largely insensitive to the final tumour size (Nend) when this value is realistically large (Nend>109) (Supplementary Figure 6 and Supplementary Note).
We note that the theoretical framework is based upon the assumption of exponential growth, which is a growth pattern well supported by empirical data in many cancer types23–25. The impact of alternate models of growth, such as logistic and Gompertzian growth, is explored in the Supplementary Note. We also implemented a cancer stem cell model where only a subset of cells has unlimited proliferation potential and found that for the purposes of this study this has little impact on the expected VAF distribution, which in this scenario only measure events that occur in the stem cell compartment (Supplementary Figure 7).
Recovery of evolutionary dynamics in synthetic tumours
First, we assessed the degree to which subclonal selection is detectable within VAF distributions by performing a frequentist power analysis to examine the conditions under which we correctly reject the null when the alternative (selection present) is true. We performed simulations to measure the values of t1 (time of subclone formation) and s (magnitude of selective advantage of subclone) that lead to observable deviations from the null neutral model (see Methods) in high depth sequencing data (100X). Only subclones that arise sufficiently early (small t1) or that were very fit (large s) were able to produce detectable deviations in the clonal composition of the tumour (Figure 1e).
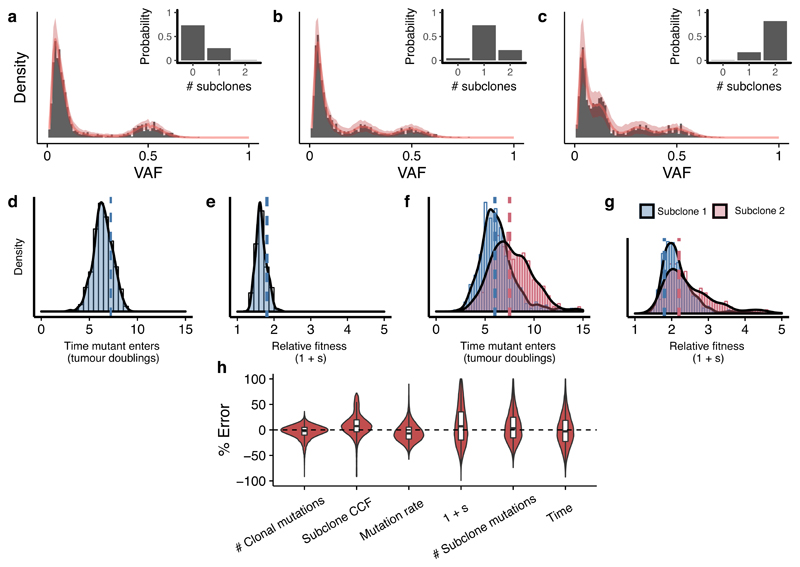
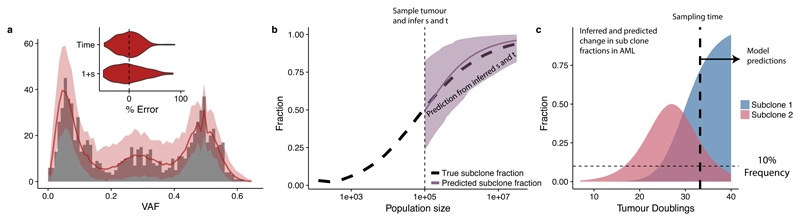
We then applied our Bayesian framework to estimate evolutionary parameters from synthetic data (VAF distributions derived from computational simulations of tumour growth with known parameters). Our framework identified the correct underlying model with high probability for representative examples of a neutrally growing tumour (Figure 2a), a tumour with a single subclone (Figure 2b) and a tumour with 2 subclones (Figure 2c), and also recovers the evolutionary parameters in each case (Figures 2d-g). Given that we modelled tumour growth as a stochastic process, variability in our estimates was expected (see Supplementary Note). In a cohort of 100 synthetic tumours (20 examples selected in Supplementary Figure 8), where the ground truth was known, the mean percentage error on parameter inference was below 10% (Figure 2h). The stochasticity also explains the width of the posterior distributions (Figures 2d-g). In particular, the rate of stochastic cell death has a large effect on the variability of lineage age and consequently can cause a slight over-estimation of the mutation rate and variability in the time taken for a lineage to clonally expand increases with increased cell death (see Supplementary Note).
Figure 2. Accurate recovery of evolutionary parameters from simulated data using Approximate Bayesian Computation.
Our method recovered the correct clonal structure in simulated tumour data for representative examples of (a) a neutral case, (b) a 1 subclone case and (c) a two subclones case. Grey bars are simulated VAF data, solid red lines indicate the median histograms from the simulations that were selected by the statistical inference framework (500 posterior samples), shaded areas are 95% intervals. The inferred posterior distributions of the evolutionary parameters contained the true values (dashed lines) for (d,f) the time of emergence of the subclones and (e,g) the selection coefficient 1+s. (h) The mean percentage error in inferred parameter values across a virtual tumour cohort (n=100 tumours) was below 10%. Boxplots show the median and inter quantile range (IQR), upper whisker is 3rd quantile + 1.5*IQR and lower whisker is 1st quantile - 1.5*IQR.
Monte Carlo analysis indicated that accurate measurement of subclonal evolutionary dynamics required high depth (>100X) for both whole-exome and whole-genome sequencing (Supplementary Figure 9). This analysis demonstrates how the clonal structure becomes progressively obscured as the sequencing depth decreases. Depths of sequencing of less than 100X preclude a robust quantification of subclonal dynamics, and moreover the neutral model is preferred by our Bayesian model selection framework, even when it is false (Supplementary Figure 9). Importantly, this analysis showed that even in some cases when selection is present (particularly weak selection), neutral evolution is the most parsimonious description of the data. In other words, the observed dynamics are then ‘effectively neutral’. In addition, we note that while the increased mutational information provided by WGS and higher sequencing depths makes quantification of subclonal structure more robust, this can also reveal (neutrally) drifting populations that may be falsely ascribed as a selected clone (Supplementary Figure 10). We also investigated the robustness of the inference method to tumour purity and cancer cell fraction of the subclone finding that at 100X sequencing depth a minimum purity of 50% is needed to confidently identify subclones with cancer cell fraction >30% (15% VAF in a diploid genome), see Supplementary Figure 11.
Detectable subclones have a large selective advantage
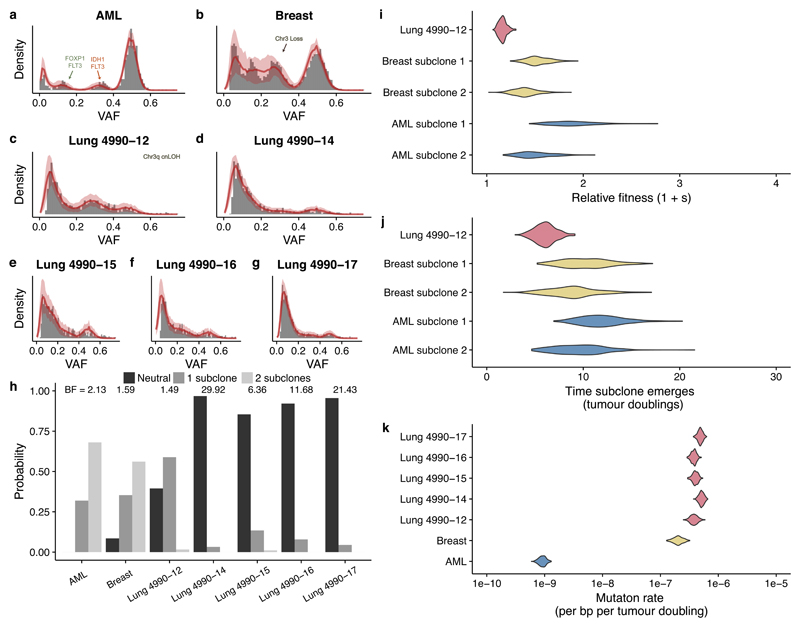
We first used our approach to quantify evolutionary dynamics in primary human cancers where high depth (>150X) and validated sequencing data were available. We considered whole-genome sequencing (WGS) of a single AML sample26, WGS of a single breast cancer sample18 and multi-region high-depth whole exome sequencing (WXS) of a lung adenocarcinoma27. To avoid the confounding effects of copy number changes, we exploited the hitchhiking principle and restricted our analysis to consider only somatic single nucleotide variants (SNVs) that were located within diploid regions (see Methods). After correction for cellularity the ‘clonal cluster’ at VAF=0.5, and a potentially complex distribution of mutations with VAF<0.5 representing the subclonal architecture were clearly observable.
The AML and breast cancer cases both showed evidence of 2 subclonal populations, corroborating the initial studies but instead finding the lowest frequency cluster to be a consequence of all within-clone neutral mutations18,26 (Figure 3a,b,h). Measurement of the evolutionary dynamics showed that for both cancers the subclones had considerably large fitness advantages (>20%, Figure 3i) and emerged within the first 15 population doublings (Figure 3j). In the AML sample, subclone 1 (highest frequency subclone) had putative driver mutations in IDH1 1 and FLT3 and subclone 2 had a distinct FLT3 mutation and a FOXP1 mutation. In the breast cancer sample, no putative driver point mutations were found in the subclonal clusters but we note that the original analysis found that subclone 1 (highest frequency subclone) had lost one copy of chromosome 13. Interestingly, the breast cancer sample also exhibited a 100-fold higher mutation rate per tumour doubling compared to the AML sample (Figure 3k). We note that our mutation rate estimate corresponds to the number of mutations per base per population doubling. Due to the high cell death and possibly differentiation in cancers (both leading to lineage extinction), doubling in volume may require several rounds of cell division. To derive the mutation rates per base per division an independent measurement of the probability β of a cell division to give rise to two surviving lineages is required (see Methods, Equation [9] and Supplementary Note). Mutational signature analysis28 of subclonal mutations provided support for the assumption of a constant mutation rate during subclone evolution (Methods and Supplementary Figure 12).
Figure 3. Quantifying selection from high-depth bulk sequencing of human cancers.
Both (a) an acute myeloid leukemia (AML) sample and (b) a breast cancer sample sequenced at whole-genome resolution showed evidence of two selected subclones. (c) In the case of a multi-region whole-exome sequenced case of lung cancer, one sample showed evidence of a single subclone whereas four other samples (d-g) from the same patient were consistent with the neutral model. Grey bars are the data, solid red lines indicate the median histograms from the simulations that were selected by the statistical inference framework (500 posterior samples), shaded areas are the 95% intervals. (h) Bayesian model selection reports the expected clonal structure for each case (Bayes Factors reported above histograms). (i) Inferred subclone fitness advantages were 20% and 80% faster than the original population. (j) Inferred times of subclone emergence indicated subclones arose within the first 15 tumour population doublings. (k) Inferred mutation rates were of the order of 10-7 mutations per base per tumour doubling in solid tumours but ~10-9 in AML, reflecting the respective differences in mutational burden between cancer types. All posterior distributions were generated from 500 samples.
In the lung adenocarcinoma case, multiple tumour regions (n=5) had been sequenced to high depth. Amongst these regions, only one region (region 12) showed strong evidence of a new subclone (Figures 3c,h, BF = 1.49) with a measured selective advantage of 30% (Figure 3j), while for all other regions a neutral evolutionary model was most probable (Figures 3d-g, BF = 6.36-29.92). Region 12 had unique copy number alterations on chromosome 3 that could plausibly have caused the subclonal expansion (Supplementary Figure 13). Together these data show spatial heterogeneity of the evolutionary dynamics within a single tumour.
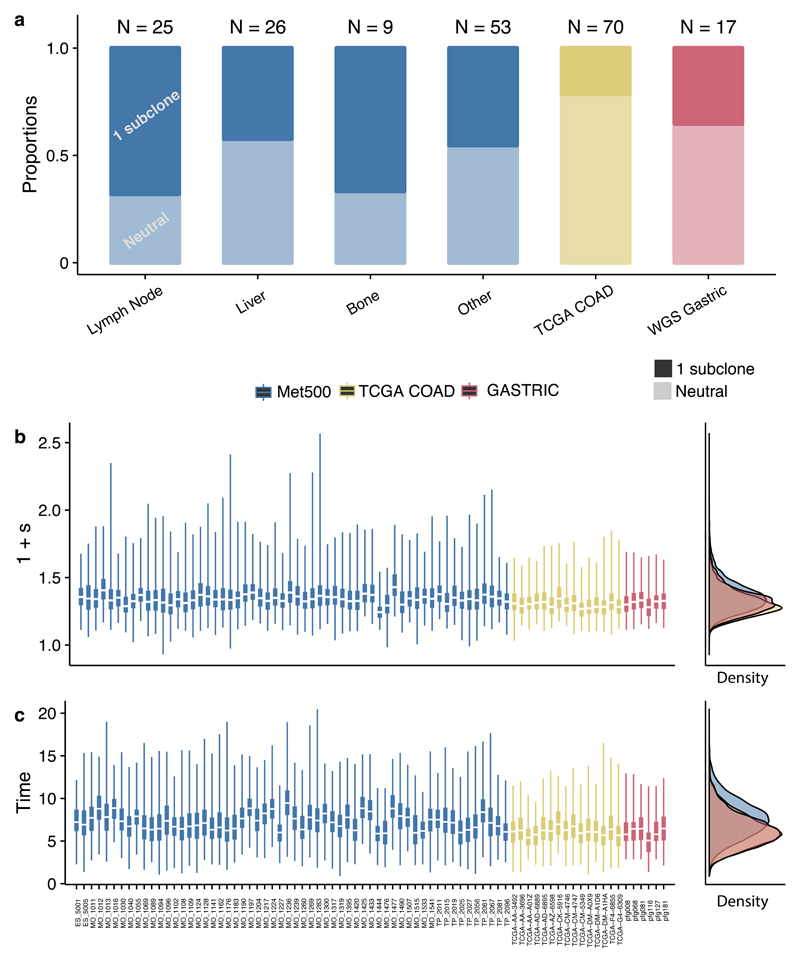
We then applied our analysis to 4 additional large cohorts of variable sequencing depth: WXS colon cancers from TCGA29 (Supplementary Figure 14), WGS gastric cancers from Wang et al30 (Supplementary Figure 15), WXS lung cancers from the TRACERx trial31 (Supplementary Figure 16), and WXS metastasis samples (multiple sites) from the MET500 cohort32 (Supplementary Figure 17). Based on our previous analysis of minimum data quality needed (see Supplementary Figure 11), we selected samples with purity >40% and number of subclonal mutations ≥25 for further analysis. Differentially selected subclones were detected in 29% (5/17 cases) of the gastric cancers and 21% (15/70 cases) of the colon cancers (Figure 4a). Interestingly the MET500 (51%, 58/113) data had a higher proportion of tumours with selected subclones. The measured selective advantage of these subclones was large (>20%) and emerged during the first few tumour doublings across all cohorts (Figures 4b,c). We note that in the metastases case, time is measured relative to the founding of the metastatic lesion, and differential selection of the subclone is measured relative to the other cells in the metastasis. Eventual founder effects in the metastasis are, by definition, clonal events in the sample, and so do not appear in the subclonal VAF spectrum. We also observed similarly large fitness advantages of subclones within the TRACERx cohort, where 97% of cases (36 out of the 37 cases suitable for our analysis) were characterised by non-neutral dynamics (Supplementary Figure 16 and 18).
Figure 4. Quantifying selection in large cohorts of primary tumours and metastatic lesions.
(a) 21% of colon cancers (N=70) from TCGA (sequenced to sufficient depth and with high enough cellularity for statistical inference), 29% of WGS gastric cancers (N=17) (data from ref.30, filtered for cellularity) and 53% of metastases (N=113) from sites had evidence of differentially selected subclones. When present, differentially selected subclones were found to have (b) large fitness advantages with respect to the host population and (c) emerge early during growth. Bayes Factors for subclonal structures for all data are reported in Supplementary Table 4. Posterior distributions were generated from 500 samples. Boxplots show the median and inter quantile range (IQR), upper whisker is 3rd quantile + 1.5*IQR and lower whisker is 1st quantile - 1.5*IQR.
Forecasting cancer evolution
Measuring the evolutionary dynamics of individual human tumours facilitates prediction on the future evolutionary trajectory of these malignancies33. Specifically, we can predict how the clonal architecture of a tumour is expected to change over time (in the absence of new drivers): such predictions could be useful, for instance, to decide how often to sample a tumour when making treatment decisions. We note we can only predict the future subclonal structure of a tumour assuming that environmental conditions stay the same – e.g. that subclone selective advantages are constant and intervention such as treatment is likely to invalidate this assumption.
Suppose a biopsy is taken and fitness of a subclone measured at some time t, we can then ask how long it will take for the subclone to become dominant (>90% frequency) in the tumour. From our model, the time for a subclone to shift from a frequency f1 to a frequency of f2 given a relative fitness advantage s is:
| [5] |
Figure 5 shows an in silico implementation of this method. The fitness advantage of a subclone was measured within a tumour at size N=105 using the Bayesian inference framework (Figure 5a), and the inferred values then use to predict subsequent growth of the subclone. The prediction well represented the ground truth (Figure 5b).
Figure 5. Predicting the future evolution of subclones.
(a) VAF distribution of an in silico tumour sampled at 105 cells was used to measure the fitness and time of emergence of a subclone. Grey bars are the simulated data, solid red lines indicate the median histograms from the simulations that were selected by the statistical inference framework (500 posterior samples), shaded areas are the 95% intervals. Inset shows error from ground truth. 500 posterior samples were taken to perform the inference. (b) These values were then used to predict the spread of the subclone as the tumour grew to 107 cells, showing the predictions matched the ground truth. Predictions were made by extrapolating the posterior distribution of 1+s using equations in the main text. Solid line shows the median value from the posterior distribution, shaded area shows the 95% interval. (c) Using the same approach in the AML sample, where we measured 1+s, t1 and t2, we would predict that subclone 2 would become dominant within 3-4 further tumour doublings while subclone 1 will become too small to be detected.
In the case of the examined AML sample (Figure 3a), the measured fitness advantages predict the future clonal structure of the malignancy (in the absence of treatment). Specifically, the larger of the two subclones present at the point when the tumour was sampled is predicted to take over the tumour, while the smaller clone is projected to become too rare to remain detectable (Figure 5c). Despite the assumption of constant conditions, our framework could be extended in the future to simulate treatment effects when those mechanisms are known.
Discussion
Here we have demonstrated how the VAF distribution can be used to directly measure evolutionary dynamics of tumour subclones. We confirmed that subclonal selection causes an overrepresentation of mutations within the expanding clone, manifested as an additional ‘peak’ in the VAF distribution, as suggested by many recent studies18,26,34. However, irrespective of subclonal selection, the tumour will still show an abundance of low frequency variants (a 1/f-like tail) as the natural consequence tumour growth, wherein the number of new mutations is proportional to the population size.
Our quantitative measurement of the selective advantage (relative fitness) of an expanding subclone revealed that detectable subclones had experienced remarkably large fitness increases, in excess of 20% greater than the background tumour population. Large increases in subclone fitness were also observed in metastatic lesions, indicating that there can still be on-going adaption even in late-stage disease, perhaps as a consequence of treatment. Because selection is inferred using only SNVs that shift in frequency due to hitchhiking, differential fitness can be measured by our analysis regardless of the underlying mechanism. Genetic driver mutations found within a subclone are one possible cause for the fitness increase.
The values of fitness advantage we infer in human malignancies are similar to reports from experimental systems. Evidence from growing human pluripotent stem cells indicates that TP53 mutants may have a fitness advantage as high as 90% (1+s=1.9)35 and that single chromosomal gains can provide a fitness advantage of up to 50%36 (range 20%-53%). A study of the competitive advantage of mutant stem cells in the mouse intestine during tumour initiation (at constant population size) showed that KRAS and APC mutant stem cells have a ~2-4 fold increased fixation probability in single crypts37 and TP53 mutant cells in mouse epidermis exhibited a 10% bias toward self-renewal38. Moreover, our inferred fitness advantages compare to large fitness advantages measured in bacteria39. Nevertheless, we acknowledge that experimental systems may differ significantly from in vivo human tumour growth and that new experimental systems are necessary to test these measurements. We also note that we are only able to measure large changes in fitness, and additional efforts will be needed to measure the complete distribution of fitness effects (DFE) within cancers. Furthermore, the inferred fitness value is sensitive to the underlying stochastic evolutionary model and thus caution is warranted in directly comparing fitness values.
Our inferred in vivo mutation rates per population doubling are also in line with experimental evidence. Seshadri et al.40 reported somatic mutation rates in normal lymphocytes of 5.5x10-8-24.6x10-8 and a 10-100 fold increase in mutation rate in cancer cell lines such as B-cell lymphoma (5.2x10-7-13.1x10-7) and ALL (66.6x10-7). A recent analysis of a mouse tumour model indicates somatic mutation rates in neoplastic cells are 11x higher than in normal tissue.
Our analysis highlights that even if cancer subclones experience pervasive weak selection, it is not sufficient to alter the clonal composition of the tumour and therefore to cause the VAF distribution to deviate detectably from the distribution expected under neutrality. It is important to note that the (initial) growth of tumours makes them peculiar evolutionary systems, as tumour growth dilutes the effects of selection41. Thus, our analysis does not discount the possibility of a multitude of ‘mini-drivers’42 but shows that these must have a corresponding ‘mini’ effect on the subclonal composition of a tumour (and that the VAF distribution in mini-driver tumours is well described by a neutral model). We note however, that the ratio of non-synonymous to synonymous variants (dN/dS), a classical test for selection, identified only a small subset of genes (<20 in a pan-cancer analysis) with extreme dN/dS values indicative of strong selection21,43.
Our previous analysis11 suggested that neutral dynamics were rejected in a higher percentage of colon cancers (approximately 65%) than the 21% reported here. The discrepancy is explained by the stochasticity in the evolutionary process where chance events can lead to deviations from the neutral 1/f distribution. Unlike our previous analytic derivation, the Bayesian model selection framework presented here captures this stochasticity (and hence neutral evolution is preferred in a greater proportion of samples).
Our measurement of evolutionary trajectories facilitates mechanistic prediction of how a tumour changes over time as demonstrated in our in silico prediction (Figure 5a,b), with implications for anticipating the dynamics of treatment resistant subclones. This may have particular value for novel evolutionary therapeutic approaches such as ‘adaptive therapy’, where the goal is to maintain the existence of competing subclones that mutually supress the growth of another44,45. Our measurements of relative clone fitness could potentially be used to optimize treatment regimes in order to maintain the coexistence of competing populations.
We acknowledge that features not described in our model, e.g. the spatial structure of the tumour, could affect the estimates of the evolutionary parameters46. Indeed, our analysis shows that there can be heterogeneity in the evolutionary process within a tumour (only 1/5 regions of a single lung tumour showed strong evidence of subclonal selection). Spatial models of tumour evolution can help elucidate other important biological parameters such as the degree of mixing within tumour cell populations, a purely spatial phenomenon which cannot be quantified using non-spatial models such as ours. We have recently shown how multiple samples per tumour increase the power to detect selection, in part because of the increased probability of sampling across a ‘subclone boundary’ where selection is evident12. We also acknowledge that complex, undetectable intermediate dynamics in the evolution of subclones, such as multiple small subclonal expansions before a subclone becomes detectable, are not modelled within our framework.
In summary, we have developed a quantitative framework to infer timing and strength of subclonal selection in vivo in human malignancies. This is a step towards enabling mechanistic prediction of cancer evolution.
Methods
Simulating tumour growth
We implement a stochastic birth-death process simulation of tumour growth, followed by a sampling scheme that recapitulates the ‘noise’ of cancer sequencing data. The sampling scheme is required to ensure that the underlying evolutionary dynamics measured from the data are not confounded by such noise. We first introduce the simulation framework for an exponentially expanding population where all cells have equal fitness, and then show how elements of the simulation are modified to include differential fitness effects and non-exponential growth (see Supplementary Note for details).
Tumour growth is assumed to begin with a single transformed cancer cell that has acquired the full set of alterations necessary for cancer expansion. In our model, this first cell will therefore be carrying a set of mutations (the number of these mutations can be modified) that will be present in all subsequent lineages, and thus appear as clonal (present in all cells and thus will generate the cluster of clonal mutations at frequency ½ for a diploid tumour) within the cancer population.
To simulate tumour, and subclone evolution, we specify a birth rate b and death rate d (b>d, for a growing population), meaning that the average population size at time t is:
| [6] |
We set b=log(2) for all simulations, such that in the absence of cell death the population will double in size at every unit of time. The tumour grows until it has reached a specified size Nend, where the simulation stops. At each division, cells acquire v new mutations, where v is drawn from a Poisson distribution with mean μ, the mutation rate per cell division. We assume new mutations are unique (infinite sites approximation). Not all divisions result in new surviving lineages because of cell death and differentiation. The probability of a cell division producing a surviving lineage β expressed can be expressed in terms of the birth and death rates:
| [7] |
Simulating subclonal selection
To include the effects of subclonal selection, a mutant is introduced into the population that has a higher net growth rate (birth minus death) than the host population. We only consider the cases of one or two subclonal populations under selection at any given time. We deem this simplification to be reasonable as the number of large-effect driver mutations in a typical cancer is thought to be small (<10 see ref44). Additionally, we found that sequencing depth >100X is required to resolve more than 1 subclone (Supplementary Figure 9). Fitter mutants can have a higher birth rate, a lower death rate, or a combination of the two, all of which results in the mutant growing at a faster rate than the host population. Given that the host/background population has growth rate bH and death rate dH, and the fitter population has growth rate bF and death rate dF, we define the selective advantage s of the fitter population as:
| [8] |
Fitter mutants can be introduced into the population with a specified selective advantage s and at a chosen time t1, allowing us to explore the relationship between the strength of selection and the time the mutant enters the population.
Simulation method and parameters
We used a rejection kinetic Monte Carlo algorithm to simulate the model45. Due to the small number of possible reactions (we consider at most 3 populations with different birth and death rates) this algorithm is more computationally efficient than a rejection-free kinetic Monte Carlo algorithm such as the Gillespie algorithm. The input parameters of the simulation are given in table 1.
Table 1. Input parameters for simulation.
| b | Birth rate within host population |
| d | Death rate within host population |
| bF | Birth rate of fitter populations, each new population will have a unique bF |
| dF | Death rate of fitter populations, each new population will have a unique dF |
| s | Selective advantage of fitter populations (calculated from bF and dF) |
| μ | Mutation rate |
| tevent | Time when fitter mutant is introduced |
| Nend | Maximum population size, simulation stops once this maximum is reached |
The simulation algorithm is as follows:
Simulation initialized with 1 cell and set all simulation parameters.
Choose a random cell, i from the population.
Draw a random number r~Uniform(0, bmax+dmax), where bmax and dmax are the maximum birth and death rates of all cells in the population.
Using r, cell i will divide with probability proportional to its birth rate bi and die with probability proportional to its death rate di. If bi+di <bmax+dmax there is a probability that cell i will neither divide nor die. If β = 1, ie no cell death then in the above dmax = 0.
If cell divides, daughter cells acquire v new mutations where v ~Poisson(μ).
Time is increased by a small increment where τ is an exponentially distributed random variable47.
Go to step 2 and repeat until population size is Nend.
The output of the simulation is a list of mutations for each cell in the final population.
Generating millions of simulations for parameter inference
A number of simplifications to our simulation scheme were made to improve computationally efficiency when used in our Bayesian inference method, a procedure that requires potentially many millions of individual simulations to be run in order to get accurate inferences. Our ultimate goal was to measure the time subclones emerge and their fitness. These parameters are measured in terms of tumour volume doublings, not in terms of cell division durations (as this is unknown in human tumours). Our approximations allow us to quantify relative fitness of subclones, measured in units of population doubling, from the VAF distribution. The approximations are:
Approximation 1: We model differential subclone fitness by varying the birth rate only, and setting the deth rate to 0 (e.g. β = 1, all lineages survive). This increases simulation speed because a smaller number of time steps are required to reach the same population size and ensures that tumours never die out in our simulations.
Timing the emergence of subclones depends on the number of mutations that have accumulated in the first cell that gave rise to the subclone. This is the product of the number of divisions and the mutation rate (n × μ), or equivalently the number of tumour doublings × the effective mutation rate Given we measure everything in terms of tumour doublings and the effective mutation rate (μ/β) is the only measure available to us from the VAF distribution (from the low frequency 1/f tail), we reduce our search space by fixing β = 1 and varying μ, recognizing that in reality the effective mutation rate is likely to have β < 1.
We do note however that cell death (β < 1) can affect our inferences in two ways. First of all, in the presence of one or more subclones, the low-frequency tail which encodes consists of a combination of two or more 1/f tails. If there are large differences in the β value between subclones, then the inference on the effective mutation rate from the gradient of the low-frequency tail may be incorrect. For example, a fitter subclone could arise due to decreased cell death rather than increased proliferation. To quantify this effect, we simulated subclones with differential fitness due to decreased cell death and measured the error on the inferred Even in cases where the death rate was dramatically different in the subclone compared to the host population (β = 1.0 vs β = 0.5) the mean error on the estimates of the mutation rate was 42% (Supplementary Figure 5), significantly less than the order of magnitude previously measured between cancer type11 and so we conclude that the constant β assumption is therefore acceptable. We do acknowledge however that we may underestimate the effects of drift, which will be accentuated in tumours with high death rates.
Approximation 2: We simulate a smaller tumour population size compared to typical tumour sizes at diagnosis, and scale the inferred values a posteriori. We note that the VAF distribution holds no information on the population size (it measures only relative proportions) and furthermore simulating realistic population sizes (in the order of tens or hundreds of billions of cells in human malignancies) is computationally unfeasible. To circumvent this, we generate synthetic datasets that capture the characteristics relevant to measuring the fitness and time subclones emerge, namely the effective mutation rate encoded by the low frequency part of the distribution, the number of mutations in any subclonal cluster and their frequency. Theoretical population genetics is then used to transform these measurements into values of fitness and time (via Equations [2] and [4]), and values are scaled by the realistic population size Nend = 1010.
Simulation length was required to allow the single cell that gives rise to the subclone sufficient time to accumulate the number of mutations ultimately observed in the empirical datum. In general, we found Nend=103 to be sufficient, except for the breast cancer and AML samples where we used the more conservative Nend=104. In general, Nend=104 is sufficient to be able to measure the range of parameters considered in Figure 1e.
To appropriately scale the estimates of s requires an estimate of the age of the tumour in terms of tumour doublings. Using Equation [4] with a final population size of Nend, we can calculate tend as:
| [10] |
where fsub is the frequency of the subclone. We assumed a realistic Nend = 1010, for generating the posterior distributions in Figures 3 & 4. We also generated posterior distributions for s as a function of Nend, for the AML, breast and lung cancers. For realistically large Nend (>109) the exact choice has minimal effect on our inferred values of s (Supplementary Figure 6).
To confirm that these assumptions do not invalidate our approach, we generated synthetic datasets with cell death and large final population size (106). We then used our inference method (detailed below) with the simplifying assumptions to infer the parameters used to generate these synthetic tumours. This demonstrated that we were able to accurately recover the input parameters when the simplifications were applied (Figure 2).
Sampling
To mimic the process of data generation by high-throughput sequencing we performed various rounds of empirically-motivated sampling of the simulation data. Sequencing data suffers from multiple sources of noise, most importantly for this study is that mutation counts (VAFs) are sampled from the true underlying frequencies in the tumour population (both because of the initial limited physical sampling of cells from the tumour for DNA extraction, and then due to the limited read depth of the sequencing). Additionally, it is challenging to discern mutations that are at low frequencies from sequencing errors, and the limited sampling of sequencing assays means that many low frequency mutations are likely not measured at all. Consequently only mutations above a frequency of around 5-10% with 100X sequencing are observable with certainty48. The ability to resolve subclonal structures is thus dependent on the depth of sequencing.
Our sampling scheme to generate synthetic datasets was as follows. For mutation i with true frequency VAFtrue, the sequence depth Di is Binomially distributed:
for a tumour of size N. The sampled read count with the mutant is Binomially distributed with the following parameters:
or if over-dispersed sequencing is modelled49,50 we use the Beta-Binomial model, which introduces additional variance to the sampling:
where ρ is the overdispersion parameter, and ρ = 0 reverts to the Binomial model. Finally, the sequenced VAF for mutation i is given by:
Modelling stem cells
Stem cell architecture was modelled with two-compartments: long lived stem cells and short lived non-stem cells. Stem cells divided symmetrically to produce two stem cells with probability α and asymmetrically to produce a single stem cell and a single differentiated cell with probability 1 − α. Differentiated cells divided n further times before dying. At each division all cells accumulated mutations as described above. We used α = 0.1 and n=5. If α = 0.1 then the model is equivalent to the above exponential growth model.
Bayesian Statistical Inference
We used Approximate Bayesian Computation (ABC) to infer the evolutionary parameters. We evaluated the accuracy of our inferences using simulated sequencing data where the true underlying evolutionary dynamics was known. The simulation approach to generate synthetic data was taken instead of a purely statistical approach, as the simulation naturally accounts for effects that would be difficult to represent in a pure statistical model (such as the convolution of multiple within subclone mutations at lower frequency ranges). Furthermore, the posterior distribution reported from this method naturally account for uncertainties due to experimental noise and stochastic effects such as Poisson-distributed mutation accumulation and stochastic birth-death processes. For in-depth discussion on these stochastic effects, see the Supplementary Note.
As in all Bayesian approaches, the goal of the ABC approach was to produce posterior distributions of parameters that give the degree of confidence that particular parameter values are true, given the data. Given a parameter vector of interest θ and data D, the aim was to compute the posterior distribution where π(θ) is the prior distribution on θ and p(D|θ) is the likelihood of the data given θ. In cases where calculating the likelihood is intractable, as was the case here where our model cannot be expressed in terms of well-known and characterized probability distributions, approximate approaches must be sought. The basic idea of these ‘likelihood free’ ABC methods is to compare simulated data, for a given set of parameter values, with observed data using a distance measure. Through multiple comparisons of different input parameter values, we can produce a posterior distribution of parameter values that minimise the distance measure, and in so doing accurately approximate the true posterior. The simplest approach is called the ABC rejection method and the algorithm is as follows51:
-
1)
Sample candidate parameters θ* from prior distribution π(θ)
-
2)
Simulate tumour growth with parameters θ*
-
3)
Evaluate distance, δ between simulated data and _target data
-
4)
If δ < ε reject parameters θ*
-
5)
If δ ≥ ε accept parameters θ*
-
6)
Return to 1
We used an extension of the simple ABC rejection algorithm, called Approximate Bayesian Computation Sequential Monte-Carlo (ABC SMC)22,52. This method achieves higher acceptance rates of candidate simulations and thus makes the algorithm more computationally efficient than the simple rejection ABC. It achieves this increased efficiency by propagating a set of ‘particles’ (sample parameter values) through a set of intermediate distributions with strictly decreasing ε until the _target εT is reached, using an approach known as sequential importance sampling53. The ABC SMC algorithm also allows for Bayesian model selection to be performed by placing a prior over models and performing inference on the joint space of models and model parameters, (m, θm). In contrast to many applications of ABC that use summary statistics, we use the full data distribution, thus avoiding issues of inconsistent Bayes factors due to loss of information54,55. For further details on the algorithm see references22 and the Supplementary Note on the specific details of our implementation. Bayes factors for all data are shown in Supplementary Tables 4 and 5. We found that the probability of neutrality was significantly correlated with our frequentist based neutrality metrics and that the inferred mutation rates were highly similar (Supplementary Figure 19).
The clonal structure of the cancer is encoded by the shape of the VAF distribution, we therefore used the Euclidean distance between the two cumulative distributions (simulated and _target datasets) for our inference.
Testing for Selection in the Frequentist paradigm
We also refined a simple analytical test in order to rapidly determine what evolutionary parameters of selection lead to an observable deviation of the VAF distribution from that expected under neutrality. Previously, we showed that under neutrality, the distribution of mutations with a frequency greater than f is given by11:
| [11] |
We fit a linear model of M(f) against 1/f and used the R2 measure of the explained variance as our measure of the goodness of fit.
Another approach is to use the shape of the curve described by Equation [5] and test whether our empirical data collapses onto this curve. To implement this approach, here we defined the universal neutrality curve Given an appropriate normalization of the data, the mutant allele frequency distribution governed by neutral growth will collapse onto this curve, although we recognize that deviations due to stochastic effects are possible. We can normalize the distribution described by Equation [5] by considering the maximum value of M(f) at f=fmin.
| [12] |
| [13] |
| [14] |
is independent of the mutation rate and the death rate and therefore allows comparison with any dataset. To compare this theoretical distribution against empirical data we used the Kolmogorov distance, Dk, the Euclidean distance between and the empirical data and the area between and the empirical data. The Kolmogorov distance Dk is the maximum distance between two cumulative distribution functions. Supplementary Figure 1 provides a summary of the different metrics.
To assess the performance of the 4 classifiers we ran 105 neutral and non-neutral simulations and compared the distribution of the test statistics for these two cases. Due to the stochastic nature of the model, not all simulations that include selection will result in subclones at a high enough frequency to be detected, therefore to accurately assess the performance of our tests we only included simulations where the fitter subpopulation was within a certain range (20% and 70% fraction of the final tumour size). All 4 test statistics showed significantly different distributions between neutral and non-neutral cases (Supplementary Figure 2). Under the null hypothesis of neutrality and a false positive rate of 5%, the area between the curves was the test statistics with the highest power (67%) to detect selection, slightly outperforming the Kolmogorov distance and Euclidean distance, with the R2 test statistics showing the poorest performance with a power of 61% (Supplementary Tables 1 and 2).
We also plotted receiver operating characteristic (ROC) curves by varying the discrimination threshold of each of the tests of selection and calculating true positive and false positive rates (using a dataset derived from simulations with subclonal populations at a range of frequencies, Supplementary Figure 3). This analysis showed that R2 had the least discriminatory power, with the other 3 performing approximately equally well (see Supplementary Table 3 for AUC). Increasing the range of allowed subclone sizes decreased the classifier performance, likely because the subclone could merge into the clonal cluster or 1/f tail when it took a more extreme size.
Code Availability Statement
Code for the simulation and inference method, frequentist based neutrality statistics and bioinformatic scripts are available at: https://marcjwilliams1.github.io/quantifying-selection
Bioinformatics analysis
Variant calls from the original studies were used for the AML data26, TRACERx31 data and MET500 data32. Our analysis of the TCGA colon cancer cohort and gastric cancers is explained in our previous publication11.For both these cohorts, we required the cellularity>0.4 to perform the analysis. For the breast cancer data18 and lung cancer data27, bam files from the original study were obtained and variants were called using Mutect256 and filtered to require at least 5 reads reporting the variants in the tumour and 0 reads in the normal. To mitigate the effects of low frequency mutations arising from paralogous regions of the genome we filtered any mutations where 75bp regions either side of the mutations had multiple BLAST hits (minimum of 100bp hit length, maximum of 3% mismatching bases).
Copy number aberrations could also potentially result in the multi-peaked distribution we observe, hence we only used mutations that were found in regions identified as diploid (and without copy-neutral LOH). The original AML study found no evidence of copy number alterations. For the TCGA colon cancer cohort we used paired SNP array data to filter out mutations falling in non-diploid regions. For the TRACERx data and MET500 data we used allele specific copy number calls provided in the original studies to filter the data. For all other datasets we applied the Sequenza algorithm to infer allele specific copy number states and estimate the cellularity57. As the original breast cancer study found evidence of subclonal copy number alterations in multiple chromosomes we only used mutations on chromosome 3 for our analysis, (Supplementary Figure 20). BAFs of regions called as copy neutral by Sequenza in the lung cancer sample were consistent with a diploid genome (Supplementary Figure 21).
We used cellularity estimated provided by the Sequenza algorithm to correct the VAFs for each individual sample. For a cellularity estimate κ, the corrected depth for variant i will be When cellularity estimates from Sequenza were unavailable (MET500 and TRACERx) we fitted the cellularity using our ABC method by including it as an additional parameter.
As noted our simulation can account for the over-dispersion of allele read counts. To measure the over-dispersion parameter ρ, we fitted a Beta-Binomial model to the clonal cluster where we know VAFtrue = 0.5. We used Markov Chain Monte Carlo (MCMC) to fit the following model to the right hand side of the clonal cluster so as to minimize the effects of the 1/f distribution or subclonal clusters:
where Di is the sequencing depth, fi is the allele read count and is the overdispersion parameter. We then used this estimate for ρ in the simulation sampling scheme. Supplementary figure 22 shows the fits to the clonal cluster for the AML data using both the Beta-Binomial and Binomial model, and supplementary table S6 reports the over-dispersion parameter for each dataset. We also used this analysis to further refine the cellularity estimate provided by sequenza, ensuring that the clonal cluster was centred at VAF = 0.5. We note that some of the over-dispersion is likely artificial and introduced by the cellularity correction.
Mutational signatures in the breast cancer sample and AML sample (Supplementary Figure 12) were identified using the deconstructSigs R package58 using the latest mutational signature probability file from COSMIC. Signature assignment was restricted to signatures known to be active in the respective cancer types. All other parameters were set to default values. To generate confidence intervals, we bootstrapped the assignment by generating 50 datasets by sampling 90% of the mutations and running the regression on each dataset, we then report the mean value and the 95% CI.
Supplementary Material
Acknowledgements
We thank Weini Huang and Kate Chkhaidze for fruitful discussions. We are grateful to Arul Chinnaiyan and Marcin Cieslik for providing us with data from the MET500 cohort, and to Suet Leung from providing access to the gastric cancer cohort. A.S. is supported by The Chris Rokos Fellowship in Evolution and Cancer and by Cancer Research UK (A22909). T.A.G. is supported by Cancer Research UK (A19771). C.P.B. is supported by the Wellcome Trust (097319/Z/11/Z). B.W. is supported by the Geoffrey W. Lewis Post-Doctoral Training fellowship. A.S. and T.A.G. are jointly supported by the Wellcome Trust (202778/B/16/Z and 202778/Z/16/Z respectively). C.C is supported by NIH R01CA182514. M.J.W is supported by a Medical Research Council student scholarship. This work was also supported by Wellcome Trust funding to the Centre for Evolution and Cancer (105104/Z/14/Z).
Footnotes
Contributions
MW wrote all simulation code and performed mathematical and bioinformatics analysis. BW performed mathematical analysis. TH performed bioinformatics analysis. MW, BW, TH, CC, CB, AS and TG analysed the data. MW, BW, CB, AS and TG wrote the paper. CB, AS and TG jointly conceived, designed, supervised and funded the study.
Data Availability Statement
Only publically available data was used in this study, and data sources and handling of these data are described above.
References
- 1.Greaves M, Maley CC. Clonal evolution in cancer. Nature. 2012;481:306–313. doi: 10.1038/nature10762. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Gay L, Baker A-M, Graham TA. Tumour Cell Heterogeneity. F1000Res. 2016;5:238–14. doi: 10.12688/f1000research.7210.1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Wang Y, et al. Clonal evolution in breast cancer revealed by single nucleus genome sequencing. Nature. 2014;512:155–160. doi: 10.1038/nature13600. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Burrell RA, Swanton C. Re-Evaluating Clonal Dominance in Cancer Evolution. Trends in Cancer. 2016 doi: 10.1016/j.trecan.2016.04.002. [DOI] [PubMed] [Google Scholar]
- 5.Durrett R. Branching Process Models of Cancer. Springer; 2015. [Google Scholar]
- 6.Marjoram P, Tavaré S. Modern computational approaches for analysing molecular genetic variation data. Nat Rev Genet. 2006;7:759–770. doi: 10.1038/nrg1961. [DOI] [PubMed] [Google Scholar]
- 7.Fu YX, Li WH. Estimating the age of the common ancestor of a sample of DNA sequences. Mol Biol Evol. 1997;14:195–199. doi: 10.1093/oxfordjournals.molbev.a025753. [DOI] [PubMed] [Google Scholar]
- 8.Tavaré S, Balding DJ, Griffiths RC, Donnelly P. Inferring coalescence times from DNA sequence data. Genetics. 1997;145:505–518. doi: 10.1093/genetics/145.2.505. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Tsao JL, et al. Colorectal adenoma and cancer divergence. Evidence of multilineage progression. The American Journal of Pathology. 1999;154:1815–1824. doi: 10.1016/S0002-9440(10)65437-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Tsao JL, et al. Genetic reconstruction of individual colorectal tumor histories. PNAS. 2000;97:1236–1241. doi: 10.1073/pnas.97.3.1236. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Williams MJ, Werner B, Barnes CP, Graham TA, Sottoriva A. Identification of neutral tumor evolution across cancer types. Nature Geneticsure. 2016;48:238–244. doi: 10.1038/ng.3489. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Sun R, et al. Between-region genetic divergence reflects the mode and tempo of tumor evolution. Nature Geneticsure. 2017;49:1015–1024. doi: 10.1038/ng.3891. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Hartl DL, Clark AG. Principles of population genetics. Sinauer; 1997. [Google Scholar]
- 14.Bozic I, et al. Accumulation of driver and passenger mutations during tumor progression. Proc Natl Acad Sci USA. 2010;107:18545–18550. doi: 10.1073/pnas.1010978107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Cheek D, Antal T. Mutation frequencies in a birth-death branching process. arXiv [Google Scholar]
- 16.Kessler DA, Levine H. Scaling Solution in the Large Population Limit of the General Asymmetric Stochastic Luria–Delbrück Evolution Process. J Stat Phys. 2014;158:783–805. doi: 10.1007/s10955-014-1143-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Durrett R. POPULATION GENETICS OF NEUTRAL MUTATIONS IN EXPONENTIALLY GROWING CANCER CELL POPULATIONS. The Annals of Applied Probability. 2013;23:230–250. doi: 10.1214/11-aap824. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Nik-Zainal S, et al. The life history of 21 breast cancers. Celll. 2012;149:994–1007. doi: 10.1016/j.cell.2012.04.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Levy SF, et al. Quantitative evolutionary dynamics using high-resolution lineage tracking. Nature. 2015 doi: 10.1038/nature14279. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Gillespie JH. Genetic Drift in an Infinite Population: The Pseudohitchhiking Model. Genetics. 2000;155:909–919. doi: 10.1093/genetics/155.2.909. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Wu C-I, Wang H-Y, Ling S, Lu X. The Ecology and Evolution of Cancer: The Ultra-Microevolutionary Process. Annu Rev Genet. 2016;50:347–369. doi: 10.1146/annurev-genet-112414-054842. [DOI] [PubMed] [Google Scholar]
- 22.Toni T, Stumpf MPH. Simulation-based model selection for dynamical systems in systems and population biology. Bioinformatics. 2010;26:104–110. doi: 10.1093/bioinformatics/btp619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Honda O, et al. Doubling time of lung cancer determined using three-dimensional volumetric software: comparison of squamous cell carcinoma and adenocarcinoma. Lung Cancer. 2009;66:211–217. doi: 10.1016/j.lungcan.2009.01.018. [DOI] [PubMed] [Google Scholar]
- 24.Peer PG, van Dijck JA, Hendriks JH, Holland R, Verbeek AL. Age-dependent growth rate of primary breast cancer. Cancer. 1993;71:3547–3551. doi: 10.1002/1097-0142(19930601)71:11<3547::aid-cncr2820711114>3.0.co;2-c. [DOI] [PubMed] [Google Scholar]
- 25.Tilanus-Linthorst MMA, et al. BRCA1 mutation and young age predict fast breast cancer growth in the Dutch, United Kingdom, and Canadian magnetic resonance imaging screening trials. Clinical Cancer Research. 2007;13:7357–7362. doi: 10.1158/1078-0432.CCR-07-0689. [DOI] [PubMed] [Google Scholar]
- 26.Griffith M, et al. Optimizing Cancer Genome Sequencing and Analysis. Cell Systems. 2015;1:210–223. doi: 10.1016/j.cels.2015.08.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Zhang J, et al. Intratumor heterogeneity in localized lung adenocarcinomas delineated by multiregion sequencing. Science. 2014;346:256–259. doi: 10.1126/science.1256930. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Alexandrov LB, et al. Signatures of mutational processes in human cancer. Nature. 2013;500:415–421. doi: 10.1038/nature12477. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Cancer Genome Atlas Network. Comprehensive molecular characterization of human colon and rectal cancer. Nature. 2012;487:330–337. doi: 10.1038/nature11252. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Wang K, et al. Whole-genome sequencing and comprehensive molecular profiling identify new driver mutations in gastric cancer. Nature Publishing Group. 2014;46:573–582. doi: 10.1038/ng.2983. [DOI] [PubMed] [Google Scholar]
- 31.Jamal-Hanjani M, et al. Tracking the Evolution of Non–Small-Cell Lung Cancer. N Engl J Med. 2017 doi: 10.1056/NEJMoa1616288. NEJMoa1616288–13. [DOI] [PubMed] [Google Scholar]
- 32.Robinson DR, et al. Integrative clinical genomics of metastatic cancer. Nature Publishing Group. 2017;548:297–303. doi: 10.1038/nature23306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Lässig M, Mustonen V, Walczak AM. Predicting evolution. Nat ecol evol. 2017;1:77. doi: 10.1038/s41559-017-0077. [DOI] [PubMed] [Google Scholar]
- 34.Shah SP, et al. The clonal and mutational evolution spectrum of primary triple-negative breast cancers. Nature. 2012;486:395–399. doi: 10.1038/nature10933. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Merkle FT, et al. Human pluripotent stem cells recurrently acquire and expand dominant negative P53 mutations. Nature. 2017:1–11. doi: 10.1038/nature22312. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Rutledge SD, et al. Selective advantage of trisomic human cells cultured in non- standard conditions. Sci Rep. 2016:1–12. doi: 10.1038/srep22828. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Vermeulen L, et al. Defining stem cell dynamics in models of intestinal tumor initiation. Science. 2013;342:995–998. doi: 10.1126/science.1243148. [DOI] [PubMed] [Google Scholar]
- 38.Klein AM, Brash DE, Jones PH, Simons BD. Stochastic fate of p53-mutant epidermal progenitor cells is tilted toward proliferation by UV B during preneoplasia. Proc Natl Acad Sci USA. 2010;107:270–275. doi: 10.1073/pnas.0909738107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Lenski RE, Travisano M. Dynamics of adaptation and diversification: a 10,000-generation experiment with bacterial populations. PNAS. 1994;91:6808–6814. doi: 10.1073/pnas.91.15.6808. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Seshadri R, Kutlaca RJ, Trainor K, Matthews C, Morley AA. Mutation rate of normal and malignant human lymphocytes. Cancer Res. 1987;47:407–409. [PubMed] [Google Scholar]
- 41.Sottoriva A, et al. A Big Bang model of human colorectal tumor growth. Nature Genetics. 2015;47:209–216. doi: 10.1038/ng.3214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Castro-Giner F, Ratcliffe P, Tomlinson I. The mini-driver model of polygenic cancer evolution. Nature Reviews Cancer. 2015:1–6. doi: 10.1038/nrc3999. [DOI] [PubMed] [Google Scholar]
- 43.Martincorena I, et al. Universal Patterns of Selection in Cancer and Somatic Tissues. Cell. 2017:1–35. doi: 10.1016/j.cell.2017.09.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Enriquez-Navas PM, et al. Exploiting evolutionary principles to prolong tumor control in preclinical models of breast cancer. Science Translational Medicine. 2016;8:327ra24–327ra24. doi: 10.1126/scitranslmed.aad7842. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Zhang J, Cunningham JJ, Brown JS, Gatenby RA. Integrating evolutionary dynamics into treatment of metastatic castrate-resistant prostate cancer. Nat Commun. 2017:1–9. doi: 10.1038/s41467-017-01968-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Fusco D, Gralka M, Kayser J, Anderson A, Hallatschek O. Excess of mutational jackpot events in expanding populations revealed by spatial Luria-Delbrück experiments. Nat Commun. 2016;7 doi: 10.1038/ncomms12760. 12760. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Waclaw B, et al. A spatial model predicts that dispersal and cell turnover limit intratumour heterogeneity. Nature. 2015 doi: 10.1038/nature14971. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Stead LF, Sutton KM, Taylor GR, Quirke P, Rabbitts P. Accurately identifying low-allelic fraction variants in single samples with next-generation sequencing: applications in tumor subclone resolution. Human Mutation. 2013;34:1432–1438. doi: 10.1002/humu.22365. [DOI] [PubMed] [Google Scholar]
- 49.Roth A, et al. PyClone: statistical inference of clonal population structure in cancer. Nat Methods. 2014;11:396–398. doi: 10.1038/nmeth.2883. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Gerstung M, et al. Reliable detection of subclonal single-nucleotide variants in tumour cell populations. Nat Commun. 2012;3:811. doi: 10.1038/ncomms1814. [DOI] [PubMed] [Google Scholar]
- 51.Pritchard JK, Seielstad MT, Perez-Lezaun A, Feldman MW. Population growth of human Y chromosomes: a study of Y chromosome microsatellites. Mol Biol Evol. 1999;16:1791–1798. doi: 10.1093/oxfordjournals.molbev.a026091. [DOI] [PubMed] [Google Scholar]
- 52.Toni T, Stumpf MPH. Simulation-based model selection for dynamical systems in systems and population biology. Bioinformatics. 2010;26:104–110. doi: 10.1093/bioinformatics/btp619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Del Moral P, Doucet A, Jasra A. Sequential Monte Carlo samplers. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 2006;68:411–436. [Google Scholar]
- 54.Robert CP, Cornuet J-M, Marin J-M. Pillai NS Lack of confidence in approximate Bayesian computation model choice. Proc Natl Acad Sci USA. 2011;108:15112–15117. doi: 10.1073/pnas.1102900108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Barnes CP, Filippi S, Stumpf MPH, Thorne T. Considerate approaches to constructing summary statistics for ABC model selection. Stat Comput. 2012;22:1181–1197. [Google Scholar]
- 56.Cibulskis K, et al. Sensitive detection of somatic point mutations in impure and heterogeneous cancer samples. Nat Biotechnol. 2013;31:213–219. doi: 10.1038/nbt.2514. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Favero F, et al. Sequenza: allele-specific copy number and mutation profiles from tumor sequencing data. Ann Oncol. 2015;26:64–70. doi: 10.1093/annonc/mdu479. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Rosenthal R, McGranahan N, Herrero J, Taylor BS, Swanton C. deconstructSigs: delineating mutational processes in single tumors distinguishes DNA repair deficiencies and patterns of carcinoma evolution. Genome Biology. 2016:1–11. doi: 10.1186/s13059-016-0893-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.