Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 1999 Sep 28;96(20):11311-6.
doi: 10.1073/pnas.96.20.11311.

A simple model for calculating the kinetics of protein folding from three-dimensional structures

V Muñoz  1 , W A Eaton
Affiliations

A simple model for calculating the kinetics of protein folding from three-dimensional structures

V Muñoz et al. Proc Natl Acad Sci U S A. .

Abstract

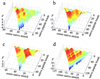
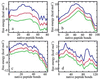
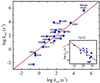
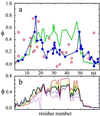
An elementary statistical mechanical model was used to calculate the folding rates for 22 proteins from their known three-dimensional structures. In this model, residues come into contact only after all of the intervening chain is in the native conformation. An additional simplifying assumption is that native structure grows from localized regions that then fuse to form the complete native molecule. The free energy function for this model contains just two contributions-conformational entropy of the backbone and the energy of the inter-residue contacts. The matrix of inter-residue interactions is obtained from the atomic coordinates of the three-dimensional structure. For the 18 proteins that exhibit two-state equilibrium and kinetic behavior, profiles of the free energy versus the number of native peptide bonds show two deep minima, corresponding to the native and denatured states. For four proteins known to exhibit intermediates in folding, the free energy profiles show additional deep minima. The calculated rates of folding the two-state proteins, obtained by solving a diffusion equation for motion on the free energy profiles, reproduce the experimentally determined values surprisingly well. The success of these calculations suggests that folding speed is largely determined by the distribution and strength of contacts in the native structure. We also calculated the effect of mutations on the folding kinetics of chymotrypsin inhibitor 2, the most intensively studied two-state protein, with some success.

PubMed Disclaimer

Figures

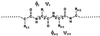
Figure 1
Figure 1
Schematic of peptide backbone showing that fixing the orientation of the CO-NH peptide plane by defining the two dihedral angles (ψi, φi+1) also defines the relative orientation of the Cα-Cβ bond vectors of residues Ri and Ri+1.
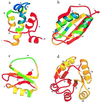
Figure 2
Figure 2
Structures of monomeric λ repressor (a), muscle acyl phosphatase (b), CI2 (c), and Che Y (d) showing by the color code the theoretical φ values for each position in the protein (see text). The φ values increase with decreasing wavelength, from red (φ = 0) to yellow (φ = 0.5) to blue (φ = 1). These φ values are calculated in the small perturbation limit, i.e., ΔRTlnK = 0.1 kcal⋅mol−1. The φ value pattern in Che Y requires some explanation because it is a three-state protein. The experiments report the φ values from unfolding kinetics (30) whereas the calculation shown here is for the folding rate from the completely denatured state. Because the N-terminal subdomain is already folded in the intermediate, the folding rate (i.e., the smaller eigenvalue) is insensitive to mutations in this area since they affect the intermediate and the transition state equally.
Figure 3
Figure 3
Free energy surfaces for monomeric λ repressor (a), muscle acyl phosphatase (b), CI2 (c), and Che Y (d). This surface is the free energy as a function of the number of native peptide bonds (j) and the position of the central residue of a contiguous stretch of native peptide bonds starting at residue i. The free energies increase with increasing wavelength from low (blue) to high (red).
Figure 4
Figure 4
Free energy profiles for monomeric λ repressor (a), muscle acyl phosphatase (b), CI2 (c), and Che Y (d). Profiles are shown in the single (blue, upper curve), double (red, middle curve), and triple (green, lower curve) sequence approximations.
Figure 5
Figure 5
Comparison of calculated and experimentally observed folding rates at zero denaturant concentration in the double sequence approximation. The observed rates are taken from the compilation by Jackson (3). The correlation coefficient in the single, double, and triple sequence approximations are 0.83, 0.85, and 0.87, respectively. In the first two, the parameters of the model were adjusted to maximize the agreement by using a least squares criterion. The rates in the triple sequence approximation were calculated with the values of the two Δsk’s and D from the double sequence approximation, and a new set of ɛ’s in order to reproduce the experimental equilibrium constants. A plot of the experimental log kf versus log K gives a correlation coefficient of 0.25, showing no significant correlation between folding rate and thermodynamic stability in this set of proteins. The inset shows a plot of the experimental rates versus the percent contact order (%CO) calculated using 0.4 nm as the cut-off-distance for the 18 two-state proteins of our study. The percent contact order defined by Plaxco et al. (19) is formula image where N is the total number of contacts, ΔSi,j is the sequence separation in residues between contacting residues i and j, and L is the total number of residues in the protein. The correlation coefficient is 0.64. The folding rate for the β-hairpin extrapolated from the least-squares line is almost 108× smaller than the experimental value. Without the length normalization (L), however, the extrapolated rate is only 30× slower.
Figure 6
Figure 6
Theoretical calculation of φ values. (a) Comparison of experimental and theoretical φ values for CI2. The experimental uncertainty in the φ values arises mainly from the uncertainty in the determination of the folding equilibrium constants. The φ values reported by Itzhaki et al. (40) were therefore divided into two groups according to the absolute magnitude of the change in folding free energy introduced by the mutation (at 4 M urea, the midpoint of the unfolding transition for the wild type). One group (filled blue circles) corresponds to φ values for mutations that cause folding free energy changes >1 kcal⋅mol−1 compared with wild-type whereas the second group (open red circles) corresponds to φ values for mutations that cause free energy changes <1 kcal⋅mol−1. In this second group, there are five negative φ values and one value >1.0, which are not plotted. Also, the value plotted for residue 16 is the one redetermined by Ladurner et al. (41). A blue line connects the filled blue circles to indicate that these values are, for the most part, better determined. Large changes in folding free energy can, however, change the φ value by changing the shape as well as the size of the free energy barrier. To investigate this effect, we used our model to calculate the dependence of the φ value for CI2 on the magnitude of the free energy change (b). These calculations show that the difference between the theoretical φ value calculated using the measured free energy change and the theoretical φ value calculated in the small perturbation limit (see Methods) is <0.1 for all residues except 29 and 47. (b) Dependence of theoretical φ values on the magnitude and sign of the free energy change produced by a mutation. The thick black line corresponds to φ values in the small perturbation limit. Dashed lines are φ values for mutations that stabilize the native state (magenta for |ΔΔG| = 3 kcal⋅mol−1; blue for |ΔΔG| = 1.5 kcal⋅mol−1), and continuous lines are for mutations that destabilize the native state (green for |ΔΔG| = 1.5 kcal⋅mol−1; yellow for |ΔΔG| = 3 kcal⋅mol−1; red for |ΔΔG| = 4.5 kcal⋅mol−1).
See this image and copyright information in PMC

Comment in

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Lansbury P T. Proc Natl Acad Sci USA. 1999;96:3342–3344. - PMC - PubMed
    1. Jackson S E, Fersht A R. Biochemistry. 1991;30:10428–10435. - PubMed
    1. Jackson S E. Fold Des. 1998;3:R81–R91. - PubMed
    1. Bryngelson J D, Wolynes P G. Proc Natl Acad Sci USA. 1987;84:7524–7528. - PMC - PubMed
    1. Onuchic J, Luthey-Schulten A, Wolynes P G. Annu Rev Phys Chem. 1997;48:545–600. - PubMed

LinkOut - more resources

  NODES
twitter 2