Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2008 Nov 27:8:79.
doi: 10.1186/1471-2288-8-79.

Undue reliance on I(2) in assessing heterogeneity may mislead

Gerta Rücker  1 , Guido Schwarzer, James R Carpenter, Martin Schumacher
Affiliations

Undue reliance on I(2) in assessing heterogeneity may mislead

Gerta Rücker et al. BMC Med Res Methodol. .

Abstract

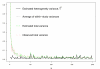
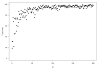
Background: The heterogeneity statistic I(2), interpreted as the percentage of variability due to heterogeneity between studies rather than sampling error, depends on precision, that is, the size of the studies included.

Methods: Based on a real meta-analysis, we simulate artificially 'inflating' the sample size under the random effects model. For a given inflation factor M = 1, 2, 3,... and for each trial i, we create a M-inflated trial by drawing a treatment effect estimate from the random effects model, using s(i)(2)/M as within-trial sampling variance.

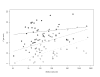
Results: As precision increases, while estimates of the heterogeneity variance tau(2) remain unchanged on average, estimates of I(2) increase rapidly to nearly 100%. A similar phenomenon is apparent in a sample of 157 meta-analyses.

Conclusion: When deciding whether or not to pool treatment estimates in a meta-analysis, the yard-stick should be the clinical relevance of any heterogeneity present. tau(2), rather than I(2), is the appropriate measure for this purpose.

PubMed Disclaimer

Figures

Figure 1
Figure 1
Top left panel: Meta-analysis of thrombolytic therapy in acute myocardial infarction [14]. Other plots: illustrative randomly sampled versions of the same meta-analysis with sample-size inflation factors of M = 4, 16 and 64 (details in text).
Figure 2
Figure 2
Within-study variation, decreasing with increasing sample size while heterogeneity remains constant. Details in text.
Figure 3
Figure 3
Percentage I2 of variation due to heterogeneity rather than to sampling error against sample size (same simulation data as in Figure 2).
Figure 4
Figure 4
I2 against median study size in a sample of 157 meta-analyses. Light, grey and black dots and regression lines correspond to the first, second and third tercile of the distribution of τ2.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Hardy RJ, Thompson SG. Detecting and describing heterogeneity in meta-analysis. Statistics in Medicine. 1998;17:841–856. doi: 10.1002/(SICI)1097-0258(19980430)17:8<841::AID-SIM781>3.0.CO;2-D. - DOI - PubMed
    1. Thompson SG, Sharp SJ. Explaining heterogeneity in meta-analysis: A comparison of methods. Statistics in Medicine. 1999;18:2693–2708. doi: 10.1002/(SICI)1097-0258(19991030)18:20<2693::AID-SIM235>3.0.CO;2-V. - DOI - PubMed
    1. Engels EA, Schmid CH, Terrin N, Olkin I, Lau J. Heterogeneity and statistical significance in meta-analysis: An empirical study of 125 meta-analyses. Statistics in Medicine. 2000;19:1707–1728. doi: 10.1002/1097-0258(20000715)19:13<1707::AID-SIM491>3.0.CO;2-P. - DOI - PubMed
    1. Higgins JPT, Thompson SG. Quantifying heterogeneity in a meta-analysis. Statistics in Medicine. 2002;21:1539–1558. doi: 10.1002/sim.1186. - DOI - PubMed
    1. Sidik K, Jonkman JN. Simple heterogeneity variance estimation for meta-analysis. JRSS Series C (Applied Statistics) 2005;54:367–384. doi: 10.1111/j.1467-9876.2005.00489.x. - DOI

Publication types

MeSH terms

  NODES
INTERN 2
twitter 2