Suppression of collapse for two-dimensional Airy beam in nonlocal nonlinear media
- PMID: 28646218
- PMCID: PMC5482803
- DOI: 10.1038/s41598-017-04095-9
Suppression of collapse for two-dimensional Airy beam in nonlocal nonlinear media
Abstract
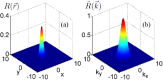
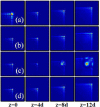
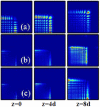
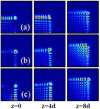
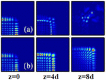
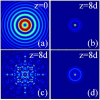
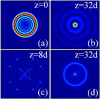
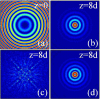
Dynamics and collapse of two-dimensional Airy beams are investigated numerically in nonlocal nonlinear media with split step Fourier transform method. In particular, the stability and self-healing properties of the Airy beams depend crucially on the location and topological charge of the vortex when the beams carry angular momentum. The propagation of abruptly autofocusing Airy beams is also demonstrated in local and nonlocal media. In strongly self-focusing regime, with the help of nonlocality, stationary propagation of two-dimensional Airy beams can be obtained, which always collapse in local nonlinear media.
Conflict of interest statement
The authors declare that they have no competing interests.
Figures
Similar articles
-
Solitons shedding from Airy beams and bound states of breathing Airy solitons in nonlocal nonlinear media.Sci Rep. 2015 Apr 22;5:9814. doi: 10.1038/srep09814. Sci Rep. 2015. PMID: 25900878 Free PMC article.
-
Terahertz circular Airy vortex beams.Sci Rep. 2017 Jun 20;7(1):3891. doi: 10.1038/s41598-017-04373-6. Sci Rep. 2017. PMID: 28634341 Free PMC article.
-
Interactions of Airy beams in nonlinear media with fourth-order diffraction.Opt Express. 2023 Apr 24;31(9):14715-14725. doi: 10.1364/OE.488852. Opt Express. 2023. PMID: 37157330
-
Controlling abruptly autofocusing vortex beams to mitigate crosstalk and vortex splitting in free-space optical communication.Opt Express. 2018 May 14;26(10):12605-12619. doi: 10.1364/OE.26.012605. Opt Express. 2018. PMID: 29801299
-
Nonlinear Beam Shaping in Domain Engineered Ferroelectric Crystals.Adv Mater. 2020 Jul;32(27):e1903775. doi: 10.1002/adma.201903775. Epub 2019 Nov 4. Adv Mater. 2020. PMID: 31682041 Review.
References
-
- Chong A, Renninger WH, Christodoulides DN, Wise FW. Airy-Bessel wave packets as versatile linear light bullets. Nat. Photon. 2010;4:103–106. doi: 10.1038/nphoton.2009.264. - DOI
Publication types
LinkOut - more resources
Full Text Sources
Other Literature Sources

