A computationally efficient physiologically comprehensive 3D-0D closed-loop model of the heart and circulation
- PMID: 34630765
- PMCID: PMC7611781
- DOI: 10.1016/j.cma.2021.114092
A computationally efficient physiologically comprehensive 3D-0D closed-loop model of the heart and circulation
Abstract
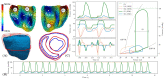
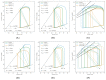
Computer models of cardiac electro-mechanics (EM) show promise as an effective means for the quantitative analysis of clinical data and, potentially, for predicting therapeutic responses. To realize such advanced applications methodological key challenges must be addressed. Enhanced computational efficiency and robustness is crucial to facilitate, within tractable time frames, model personalization, the simulation of prolonged observation periods under a broad range of conditions, and physiological completeness encompassing therapy-relevant mechanisms is needed to endow models with predictive capabilities beyond the mere replication of observations. Here, we introduce a universal feature-complete cardiac EM modeling framework that builds on a flexible method for coupling a 3D model of bi-ventricular EM to the physiologically comprehensive 0D CircAdapt model representing atrial mechanics and closed-loop circulation. A detailed mathematical description is given and efficiency, robustness, and accuracy of numerical scheme and solver implementation are evaluated. After parameterization and stabilization of the coupled 3D-0D model to a limit cycle under baseline conditions, the model's ability to replicate physiological behaviors is demonstrated, by simulating the transient response to alterations in loading conditions and contractility, as induced by experimental protocols used for assessing systolic and diastolic ventricular properties. Mechanistic completeness and computational efficiency of this novel model render advanced applications geared towards predicting acute outcomes of EM therapies feasible.
Keywords: Frank–Starling mechanism; Ventricular load; Ventricular pressure–volume relation.
Conflict of interest statement
Declaration of competing interest The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Figures
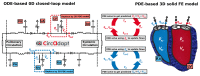

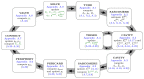
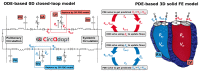
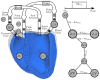


Similar articles
-
A Modular Framework for Implicit 3D-0D Coupling in Cardiac Mechanics.Comput Methods Appl Mech Eng. 2024 Mar 1;421:116764. doi: 10.1016/j.cma.2024.116764. Epub 2024 Jan 19. Comput Methods Appl Mech Eng. 2024. PMID: 38523716
-
A monolithic 3D-0D coupled closed-loop model of the heart and the vascular system: Experiment-based parameter estimation for patient-specific cardiac mechanics.Int J Numer Method Biomed Eng. 2017 Aug;33(8):e2842. doi: 10.1002/cnm.2842. Epub 2017 Feb 16. Int J Numer Method Biomed Eng. 2017. PMID: 27743468
-
Computer simulated modeling of healthy and diseased right ventricular and pulmonary circulation.J Clin Monit Comput. 2018 Dec;32(6):1015-1024. doi: 10.1007/s10877-018-0099-2. Epub 2018 Jan 12. J Clin Monit Comput. 2018. PMID: 29330837
-
Cardiovascular modeling in pulmonary arterial hypertension: focus on mechanisms and treatment of right heart failure using the CircAdapt model.Am J Cardiol. 2012 Sep 15;110(6 Suppl):39S-48S. doi: 10.1016/j.amjcard.2012.06.015. Am J Cardiol. 2012. PMID: 22921031 Review.
-
Cardiophysiology Illustrated by Comparing Ventricular Volumes in Healthy Adult Males and Females.Adv Exp Med Biol. 2018;1065:123-138. doi: 10.1007/978-3-319-77932-4_8. Adv Exp Med Biol. 2018. PMID: 30051381 Review.
Cited by
-
Simulating impaired left ventricular-arterial coupling in aging and disease: a systematic review.Biomed Eng Online. 2024 Feb 22;23(1):24. doi: 10.1186/s12938-024-01206-2. Biomed Eng Online. 2024. PMID: 38388416 Free PMC article.
-
Computational models of ventricular mechanics and adaptation in response to right-ventricular pressure overload.Front Physiol. 2022 Aug 24;13:948936. doi: 10.3389/fphys.2022.948936. eCollection 2022. Front Physiol. 2022. PMID: 36091369 Free PMC article. Review.
-
Approaches to vascular network, blood flow, and metabolite distribution modeling in brain tissue.Biophys Rev. 2023 Aug 18;15(5):1335-1350. doi: 10.1007/s12551-023-01106-0. eCollection 2023 Oct. Biophys Rev. 2023. PMID: 37974995 Free PMC article. Review.
-
Mechanoelectric effects in healthy cardiac function and under Left Bundle Branch Block pathology.Comput Biol Med. 2023 Apr;156:106696. doi: 10.1016/j.compbiomed.2023.106696. Epub 2023 Feb 24. Comput Biol Med. 2023. PMID: 36870172 Free PMC article.
-
Sequential Coupling Shows Minor Effects of Fluid Dynamics on Myocardial Deformation in a Realistic Whole-Heart Model.Front Cardiovasc Med. 2021 Dec 23;8:768548. doi: 10.3389/fcvm.2021.768548. eCollection 2021. Front Cardiovasc Med. 2021. PMID: 35004885 Free PMC article.
References
-
- Laslett LJ, Alagona P, Clark BA, Drozda JP, Saldivar F, Wilson SR, Poe C, Hart M. The worldwide environment of cardiovascular disease: Prevalence, diagnosis, therapy, and policy issues: A report from the American College of Cardiology. J Am Coll Cardiol. 2012;60(25 Supplement):S1–S49. - PubMed
-
- Timmis A, Townsend N, Gale CP, Torbica A, Lettino M, Petersen SE, Mossialos EA, Maggioni AP, Kazakiewicz D, May HT, et al. European society of cardiology: Cardiovascular disease statistics 2019. Eur Heart J. 2020;41(1):12–85. - PubMed
-
- Wilkins E, Wilson L, Wickramasinghe K, Bhatnagar P, Leal J, Luengo-Fernandez R, Burns R, Rayner M, Townsend N. European Cardiovascular Disease Statistics 2017. European Heart Network. 2017
Grants and funding
LinkOut - more resources
Full Text Sources
