Abstract
Skeleton-based action recognition has drawn much attention recently. Previous methods mainly focus on using RNNs or CNNs to process skeletons. But they ignore the topological structure of the skeleton which is very important for action recognition. Recently, Graph Convolutional Networks (GCNs) achieve remarkable performance in modeling non-Euclidean structures. However, current graph convolutional networks lack the capacity of modeling hierarchical information, which may be sub-optimal for classifying actions which are performed in a hierarchical way. In this work, a novel Hierarchical Graph Convolutional Network (HiGCN) is proposed to deal with these problems. The proposed model includes several Hierarchical Graph Convolutional Layers (HiGCLs). Each layer consists of an attention block and a hierarchical graph convolutional block, which are used for salient feature enhancement and hierarchical representation learning, respectively. To represent hierarchical information of human actions, we propose a graph pooling method, which is differentiable and can be plugged into GCN in an end-to-end manner. Extensive experiments on two benchmark datasets show the state-of-the-art performance of our method.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Action recognition is a fundamental task in computer vision with many applications such as robotics, video surveillance, etc. [11]. Due to the development of depth sensors and pose estimation methods [13], skeleton-based action recognition has drawn much attention recently. Different from other modalities, human skeletons only focus on spatial configurations and temporal evolution of human poses, which are robust to variations of viewpoints, body scales and motion speeds [20].
The main challenge of skeleton-based action recognition is how to model the spatial-temporal patterns of skeletons. Recent methods mainly rely on deep models, e.g., Recurrent Neural Networks (RNNs) [3, 17] and Convolutional Neural Networks (CNNs) [2, 5, 7], which are suitable for regular representations, e.g., sequential data and images. However, if we view spatial-temporal connections between body joints as a graph, the RNNs and CNNs may be not enough to handle the graph-shaped topology of skeleton.
Recently, Graph Convolutional Networks (GCNs) are applied to various applications [1, 6] with graph-shaped data, and obtains impressive performances. Two recent works in [22] and [9] first propose to employ the graph convolutional networks to automatically learn the spatial-temporal patterns of human skeletons. They construct a spatial graph based on the physical structure of human body and add temporal connections between corresponding joints in adjacent frames. Nevertheless, these methods only focus on the spatial-temporal patterns of body joints, ignoring the hierarchical information, i.e., the movement of human body parts in action recognition. Moreover, graph convolutional networks inherently lack the capacity of modeling hierarchical structure [23], which restricts the ability of predicting action labels for entire graph.
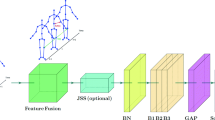
To address these limitations, we propose a novel Hierarchical Graph Convolutional Network (HiGCN). The proposed model is the stack of several Hierarchical Graph Convolutional Layers (HiGCLs), each of which consists of an attention block and a hierarchical graph convolutional block. The attention block is added first to emphasize the salient spatial-temporal nodes of skeletons. The hierarchical graph convolutional block is designed to model hierarchical information of human actions, the main idea is shown in Fig. 1. Specifically, it has two branches. One branch is a regular graph convolutional layer for modeling spatial-temporal patterns of body joints, and another branch consists of two graph pooling layers and a graph convolutional layer for hierarchical representation learning and reasoning.
Our contributions are summarized below:
-
We present a novel hierarchical graph convolutional network, i.e., HiGCN, which can model the spatial-temporal patterns of skeletons in a hierarchical way.
-
We propose a graph pooling method which can be elegantly plugged into GCN in an end-to-end manner.
-
Our method obtains the state-of-the-art results on two widely used benchmarks.
2 Method
In this section, the overall framework of Hierarchical Graph Convolutional Network (HiGCN) is introduced. In Sect. 2.1, we briefly introduce the original spatial-temporal graph convolutional network. In Sect. 2.2, we describe the proposed hierarchical graph convolution networks in detail.
2.1 Preliminaries
We consider an undirected graph \(\mathcal {G}=\{\mathcal {V},\mathcal {E}\}\), where \(\mathcal {V}\) is the set of vertices and \(\mathcal {E}\) is the set of edges. Let \(\varvec{A}\) denotes the adjacency matrix, whose element \(a_{ij}\) is the weight assigned to the edge (\(i, j\)). We set \(a_{ij}=1\) if vertices i and j are connected and \(a_{ij}=0\) otherwise. For the skeleton sequence, a spatial-temporal graph is constructed based on the physical structure of human body and chronological order.
Here, we adopt the similar implementation of graph convolution as in [6]. For spatial dimension, the graph convolution operation at layer \(l\) can be formulated as:
where \(\varvec{H}^{(l)}\in \mathbb {R}^{T \times V \times C_{in}}\) and \(\varvec{H}^{(l+1)}\in \mathbb {R}^{T \times V \times C_{out}}\) are the input feature and the output feature, respectively. \(C_{*}\) denotes the number of channels, \(T\) denotes the sequence length and \(V\) denotes the number of joints. \(\varvec{\widetilde{A}} =\varvec{A}+\varvec{I}_{V}\) and \(\varvec{\widetilde{D}} \in \mathbb {R}^{V \times V}\) is the degree matrix, whose element \(\widetilde{d}_{ii}=\sum _{j}\widetilde{a}_{ij}\). We also adopt the partition strategy, which is similar to the sampling function in CNN. However, different from [22], we employ the distance partitioning, which can be applied to any graph rather than skeletons. For temporal dimension, it is straightforward to perform graph convolution similar to the regular convolution. Specifically, we utilize a \(K_{t}\times 1\) convolution to simulate the temporal graph convolution operation. For more details, please refer to [22].
2.2 Hierarchical Graph Convolutional Network
The proposed hierarchical graph convolutional network mainly consists of several hierarchical graph convolutional layers (HiGCLs). The framework of a HiGCL is shown in Fig. 3, and the details are described as follows.
Input Features: Inspired by [15], we try to utilize more powerful features as input. We concatenate the original coordinates, relative coordinates as well as the temporal displacement into a new feature, we denote it as Hybrid Features. The effect of Hybrid Features will be evaluated in Sect. 3.
Graph Attention Block: Before feeding the feature for hierarchical representation learning, an additional attention block is employed to highlight the discriminative nodes. The overview of graph attention block is shown in Fig. 2. We first aggregate channel information of the input feature \(\varvec{H} \in \mathbb {R}^{T \times V \times C}\) by employing the average pooling and max pooling operation. The generated features \(\varvec{H}_{avg}\) and \(\varvec{H}_{max}\) are concatenated to form a spatial-temporal descriptor \(\varvec{H}_{att} \in \mathbb {R}^{T \times V \times 2}\). The descriptor is forwarded to a spatial-temporal graph convolutional block. We utilize the sigmoid function to make the values of the attention map to be between 0 and 1. During multiplication, the spatial-temporal attention map \(\varvec{M}_{st} \in \mathbb {R}^{T \times V \times 1}\) is broadcasted along channel dimension. In addition, we employ the skip connection to preserve information of the input feature. The whole attention process is represented as:
where \(\otimes \) is the Hadamard product, and \(\varvec{H}^{'} \in \mathbb {R}^{T \times V \times C}\) is the refined feature.
Hierarchical Graph Convolutional Block: The recent GCN-based approaches [9, 15, 22] focus on modeling spatial-temporal patterns of body joints. However, human actions are always performed in a hierarchical way. For example, we can easily distinguish wave from kick ball only by the movement of body parts, but for some fine-grained classes, e.g., reading and writing, we need more discriminative information such as the movement of body joints. Nevertheless, current graph convolutional networks lack such capacity of modeling hierarchical information.
To solve the above problem, we propose a hierarchical graph convolutional block which aims at modeling spatial-temporal evolutions of body joints and body parts in a two branch fashion, as illustrated in Fig. 3(a). The first branch is a regular graph convolutional network, which decouples the spatial-temporal graph convolution into two successive convolutional components. The second branch aims to explore the spatial-temporal relationship in a hierarchical way. Thus we need a pooling operation over graph to aggregate the nodes into super nodes.
(a) The overview of Hierarchical Graph Convolutional Layer (HiGCL). The HiGCL mainly consists of an attention block and a hierarchical graph convolutional block. (b) The spatial-temporal graph convolutional network. Here we adopt the distance partitioning in [22].
Inspired by [23], we develop a graph pooling operation which can learn hierarchical representations of graph in an end-to-end fashion. Let \(\varvec{H} \in \mathbb {R}^{V_{in} \times C}\)Footnote 1 represents the input feature of graph pooling layer. \(C\) denotes the number of channels, and \(V_{in}\) denotes the number of nodes. The graph pooling operation aims to aggregate feature \(\varvec{H}\) into compact feature \(\varvec{H}_{p}\in \mathbb {R}^{V_{out} \times C}\), where \(V_{out}\) denotes the number of pooled nodes. In general, we need \(V_{out}<V_{in}\). We propose to generate the pooling matrix as:
where \(\varvec{P} \in \mathbb {R}^{V_{in} \times V_{out}}\) is the learned pooling matrix, \(\mathcal {G}(\cdot ,\cdot )\) is graph convolution operation and \(\varvec{A}\) is the adjacency matrix. \(Relu(\cdot )\) is utilized for meeting the definition of pooling operation. However, different from other types of data, graph data has to take into account the intrinsic geometrical structure. Especially, it is essential to learn a new adjacency matrix after pooling for down-stream graph convolutional layers. For human body, it is easy to find a hierarchical structure, i.e., body joints and body parts. A body part can be viewed as an abstraction of several body joints, which means we can aggregate the nodes of body joints into the nodes of body parts. Moreover, the physical relation between body parts are obvious, so we can easily construct a new adjacency matrix for further reasoning the relation between human body parts.
Specifically, we manually define a mask \(\varvec{M} \in \mathbb {R}^{V_{in} \times V_{out}}\), whose element \(m_{ij} \in \{0, 1\}\). The rows of mask \(\varvec{M}\) are one-hot vectors, and each column of \(\varvec{M}\) represents one body part. \(m_{ij}=1\) means that the i-th joint belongs to the j-th body part, not vice versa. According to the physical structure of human body, we define several major body parts, i.e., torso, two arms and two legs. The pooling operation is formulated as:
where \(\varvec{P}\) is the same as in Eq. (3), \(\varvec{1} \in \mathbb {R}^{V_{in} \times V_{out}}\) is a matrix whose elements are all 1. \(n\) is a large negative number, we set it as \(-9\times 10^5\) in experiments. The softmax operation is implemented in a column-wise fashion. After graph pooling, the features of nodes are projected into a part-level space, and the pooled nodes have explicit semantic information.
We introduce the pooling method into the second branch for modeling hierarchical information. Specifically, the second branch includes two graph pooling layers and a spatial-temporal graph convolutional block, as shown in Fig. 3(a). The first pooling layer aggregates body joints into body parts for each frame, and the graph convolutional block is used for reasoning spatial-temporal relation of body parts. The new adjacency matrix are constructed based on the physical relation between body parts. The second pooling layer outputs a body-level feature, which is global-aware and discriminative. The outputs of two branches and an identity mapping of the input are summed up to form the output of the HiGCL.
3 Experiment
In this section, we first introduce the implementation details. Then, we compare our method with several state-of-the-art methods on two benchmark datasets. Next, we comprehensively investigate some ablation studies. Finally, we visualize the learned attention maps.
3.1 Datasets
NTU RGB+D [12]: This dataset consists of 56880 actions with 60 classes. The benchmark evaluations include Cross-Subject (CS) and Cross-View (CV). In the CS evaluation, training samples come from one subset of actors and networks are evaluated on samples from remaining actors. In the CV evaluation, samples captured from cameras 2 and 3 are utilized for training, while samples from camera 1 are employed for testing.
Northwestern-UCLA dataset (N-UCLA) [19]: This dataset contains 1494 videos of 10 actions. These actions are performed by 10 subjects, repeated 1 to 6 times. Each subject has 20 joints. There are three views in this dataset. Usually, two of the views are used for training and the other one is used for testing.
3.2 Implementation Details
The proposed hierarchical graph convolutional network is the stack of nine hierarchical graph convolutional layers. Before the first HiGCL, an embedding layer is employed to project the dimension of the input feature to 64. The number of output channels for each layer are 64, 64, 64, 128, 128, 128, 256, 256 and 256, respectively. After that, a global average pooling layer is performed and the final output is feeded to a fully connection layer and a softmax layer to get the prediction. The batch size is set to 64 for NTU RGB+D and 16 for N-UCLA. The learning rates for both datasets are 0.1 initially, reduced by 0.1 after 20 epochs and 50 epochs. The training procedure stops at 80 epochs.
3.3 Experimental Results
Comparison with the State-of-the-Art Methods. The experiments of our method on two widely used benchmark datasets (NTU RGB+D [12] and N-UCLA [19]) are shown in Tables 1 and 2, respectively. We first compare our method [16] with traditional method based on hand-crafted features. As we can see, our method significantly outperforms these approaches, which shows the superiority of deep learning methods over hand-crafted approaches. Then our method is compared with recent deep learning methods. We can see that our method outperforms the state-of-the-arts on both datasets. Specifically, our method achieves the highest accuracy of 87.9% and 93.8% using CS and CV protocols respectively on NTU RGB+D, and obtains the best performance 85.4% for V2 setting and 83.9% for Average setting on N-UCLA. Note that, the performance of ESV (Synthesized+Pre-trained) [10] is higher than ours on the N-UCLA dataset. However, they synthesize more data for training and benefit from the pre-trained model on large scale image datasets. By contrast, our method is trained from scratch and we can achieve better performance compared with ESV which is trained from scratch only using the original data.
Evaluation of Components of HiGCN. We evaluate several components in our network to show their effectiveness on skeleton-based action recognition. We give the results on the NTU RGB+D dateset as shown in Table 3. As we can see, our method significantly improves the performances by 6.4% in cross-subject and 5.5% in cross-view over the baseline model, i.e., ST-GCN [22]. Even without the Hybrid Features, our method still outperforms the baseline model. Moreover, after the removal of the attention block and the hierarchical block, the performances drop significantly, indicating the two proposed blocks are very useful for action recognition.
Visualization of Attention Maps. Visualization of attention maps of the first three HiGCLs is shown in Fig. 4. We find that the attention maps gradually fucus on the salient spatial-temporal patterns. This demonstrates that the attention maps at the later layers can effectively capture important spatial-temporal information of the skeleton sequence.
4 Conclusion
In this paper, we have proposed a novel Hierarchical Graph Convolutional Network (HiGCN) for skeleton-based action recognition. The construction of HiGCN is mainly based on the Hierarchical Graph Convolutional Layers (HiGCLs). The HiGCL is comprised of an attention block and a hierarchical graph convolutional block. We have evaluated our HiGCN on two publicly available datasets, i.e., NTU RGB+D and Northwestern-UCLA, and achieved the state-of-the-art performance on both datasets. We also show the effectiveness of different components of our method based on the experimental analysis. In the future we plan to focus more on modeling temporal dynamics of actions.
Notes
- 1.
We omit temporal dimension for simplicity.
References
Defferrard, M., Bresson, X., Vandergheynst, P.: Convolutional neural networks on graphs with fast localized spectral filtering. In: Advances in Neural Information Processing Systems, pp. 3844–3852 (2016)
Du, Y., Fu, Y., Wang, L.: Skeleton based action recognition with convolutional neural network. In: Asian Conference on Pattern Recognition, pp. 579–583. IEEE (2015)
Du, Y., Fu, Y., Wang, L.: Representation learning of temporal dynamics for skeleton-based action recognition. IEEE Trans. Image Process. 25, 3010–3022 (2016)
Du, Y., Wang, W., Wang, L.: Hierarchical recurrent neural network for skeleton based action recognition. In: IEEE Conference on Computer Vision and Pattern Recognition, pp. 1110–1118. IEEE (2015)
Kim, T.S., Reiter, A.: Interpretable 3d human action analysis with temporal convolutional networks. In: IEEE Conference on Computer Vision and Pattern Recognition Workshops, pp. 1623–1631. IEEE (2017)
Kipf, T.N., Welling, M.: Semi-supervised classification with graph convolutional networks. arXiv preprint arXiv:1609.02907 (2016)
Li, C., Zhong, Q., Xie, D., Pu, S.: Skeleton-based action recognition with convolutional neural networks. In: IEEE International Conference on Multimedia & Expo Workshops, pp. 597–600. IEEE (2017)
Li, C., Zhong, Q., Xie, D., Pu, S.: Co-occurrence feature learning from skeleton data for action recognition and detection with hierarchical aggregation. In: International Joint Conference on Artificial Intelligence, pp. 786–792 (2018)
Li, C., Cui, Z., Zheng, W., Xu, C., Yang, J.: Spatio-temporal graph convolution for skeleton based action recognition. arXiv preprint arXiv:1802.09834 (2018)
Liu, M., Liu, H., Chen, C.: Enhanced skeleton visualization for view invariant human action recognition. Pattern Recogn. 68, 346–362 (2017)
Poppe, R.: A survey on vision-based human action recognition. Image Vis. Comput. 28, 976–990 (2010)
Shahroudy, A., Liu, J., Ng, T.T., Wang, G.: Ntu rgb+d: A large scale dataset for 3d human activity analysis. In: IEEE Conference on Computer Vision and Pattern Recognition, pp. 1010–1019. IEEE (2016)
Shotton, J., et al.: Real-time human pose recognition in parts from single depth images. In: IEEE Conference on Computer Vision and Pattern Recognition, pp. 1297–1304. IEEE (2011)
Si, C., Jing, Y., Wang, W., Wang, L., Tan, T.: Skeleton-based action recognition with spatial reasoning and temporal stack learning. arXiv preprint arXiv:1805.02335 (2018)
Thakkar, K., Narayanan, P.: Part-based graph convolutional network for action recognition. arXiv preprint arXiv:1809.04983 (2018)
Vemulapalli, R., Arrate, F., Chellappa, R.: Human action recognition by representing 3d skeletons as points in a lie group. In: IEEE Conference on Computer Vision and Pattern Recognition, pp. 588–595. IEEE (2014)
Wang, H., Wang, L.: Modeling temporal dynamics and spatial configurations of actions using two-stream recurrent neural networks. In: IEEE Conference on Computer Vision and Pattern Recognition, pp. 499–508. IEEE (2017)
Wang, J., Liu, Z., Wu, Y., Yuan, J.: Learning actionlet ensemble for 3d human action recognition. IEEE Trans. Pattern Anal. Mach. Intell. 36, 914–927 (2014)
Wang, J., Nie, X., Xia, Y., Wu, Y., Zhu, S.C.: Cross-view action modeling, learning and recognition. In: IEEE Conference on Computer Vision and Pattern Recognition, pp. 2649–2656. IEEE (2014)
Wang, P., Li, W., Ogunbona, P., Wan, J., Escalera, S.: Rgb-d-based human motion recognition with deep learning: a survey. Comput. Vis. Image Understand. 171, 118–139 (2017)
Xia, L., Chen, C.C., Aggarwal, J.K.: View invariant human action recognition using histograms of 3d joints. In: IEEE Conference on Computer Vision and Pattern Recognition Workshops, pp. 20–27. IEEE (2012)
Yan, S., Xiong, Y., Lin, D.: Spatial temporal graph convolutional networks for skeleton-based action recognition. arXiv preprint arXiv:1801.07455 (2018)
Ying, Z., You, J., Morris, C., Ren, X., Hamilton, W., Leskovec, J.: Hierarchical graph representation learning with differentiable pooling. In: Advances in Neural Information Processing Systems, pp. 4801–4811 (2018)
Zhang, S., Liu, X., Xiao, J.: On geometric features for skeleton-based action recognition using multilayer lstm networks. In: IEEE Winter Conference on Applications of Computer Vision, pp. 148–157. IEEE (2017)
Acknowledgements
This work is jointly supported by National Key Research and Development Program of China (2016YFB1001000), National Natural Science Foundation of China (61525306, 61633021, 61721004, 61420106015, 61806194), Capital Science and Technology Leading Talent Training Project (Z181100006318030), Beijing Science and Technology Project (Z181100008918010), and CAS-AIR.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
Huang, L., Huang, Y., Ouyang, W., Wang, L. (2019). Hierarchical Graph Convolutional Network for Skeleton-Based Action Recognition. In: Zhao, Y., Barnes, N., Chen, B., Westermann, R., Kong, X., Lin, C. (eds) Image and Graphics. ICIG 2019. Lecture Notes in Computer Science(), vol 11901. Springer, Cham. https://doi.org/10.1007/978-3-030-34120-6_8
Download citation
DOI: https://doi.org/10.1007/978-3-030-34120-6_8
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-34119-0
Online ISBN: 978-3-030-34120-6
eBook Packages: Computer ScienceComputer Science (R0)