Landscape-Scale Aboveground Biomass Estimation in Buffer Zone Community Forests of Central Nepal: Coupling In Situ Measurements with Landsat 8 Satellite Data
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Field Measurements
2.3. Field-Based AGB
2.4. Image Acquisition and Data Processing
2.5. Deriving Spectral Data and Vegetation Indices
2.6. Modeling Methods and Model Precision Assessment
2.6.1. Multiple Linear Regression
2.6.2. Random Forest
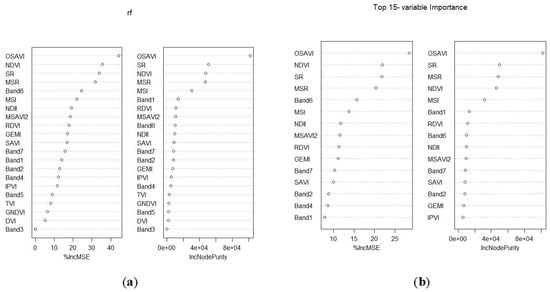
2.6.3. Variable Selection using Random Forest
2.6.4. The Effectiveness of MLR and RF in Predicting the AGB of BZCFs
3. Results
3.1. Field-Based AGB Estimates
3.2. AGB Estimates using Landsat OLI Based on the MLR
3.3. AGB Estimates using Pooled Data and Model Selected Predictor Variables Based on the RF Algorithm
4. Discussion
5. Conclusions
- Improvements in the medium-resolution Landsat 8 OLI have the potential to satisfactorily predict biomass in subtropical forest areas exhibiting flat terrain but complex forest characteristics.
- Important variables’ selection from pooled data derived from Landsat 8 OLI using the RF model yielded better results with the lowest observed RMSE value when compared to the MLR model.
- The RF model selected the Landsat 8 OLI-derived OSAVI, SR, and MSR as the most suitable variables for estimating AGB, whereas MLR selected Band 5 (NIR) and SR.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ebregt, A.; Greve, P.D. Buffer Zones and Their Management: Policy and Best Practices for Terrestrial Ecosystems in Developing Countries; Theme Studies Series; National Reference Centre for Nature Management: Wageningen, The Netherlands, 2000. [Google Scholar]
- Stræde, S.; Treue, T. Beyond buffer zone protection: A comparative study of park and buffer zone products’ importance to villagers living inside Royal Chitwan National Park and to villagers living in its buffer zone. J. Environ. Manag. 2006, 78, 251–267. [Google Scholar] [CrossRef] [PubMed]
- Baral, S. Mapping Carbon Stock Using High-Resolution Satellite Images in the Sub-Tropical Forest of Nepal. Master’s Thesis, University of Twente, Enschede, The Netherlands, 2011. [Google Scholar]
- Lu, D. Aboveground biomass estimation using Landsat TM data in the Brazilian Amazon. Int. J. Remote Sens. 2005, 26, 2509–2525. [Google Scholar] [CrossRef]
- Patenaude, G.; Milne, R.; Dawson, T.P. Synthesis of remote sensing approaches for forest carbon estimation: Reporting to the Kyoto Protocol. Environ. Science Policy 2005, 8, 161–178. [Google Scholar] [CrossRef]
- Clark, M.L.; Roberts, D.A.; Ewel, J.J.; Clark, D.B. Estimation of tropical rain forest aboveground biomass with small-footprint lidar and hyperspectral sensors. Remote Sens. Environ. 2011, 115, 2931–2942. [Google Scholar] [CrossRef]
- Chen, J.; Gu, S.; Shen, M.; Tang, M.; Matsushita, B. Estimating aboveground biomass of grassland having a high canopy cover: An exploratory analysis of in situ hyperspectral data. Int. J. Remote Sens. 2009, 30, 6497–6517. [Google Scholar] [CrossRef]
- Dube, T.; Mutanga, O.; Abdel-Rahman, E.M. Predicting Eucalyptus spp. stand volume in Zululand, South Africa: an analysis using a stochastic gradient boosting regression ensemble with multi-source data sets. Int. J. Remote Sens. 2015, 36, 3751–3772. [Google Scholar] [CrossRef]
- Mutanga, O.; Adam, E.; Cho, M.A. High-density biomass estimation for wetland vegetation using Worldview-2 imagery and random forest regression algorithm. Int. J. Appl. Earth Obs. Geoinf. 2012, 18, 399–406. [Google Scholar] [CrossRef]
- Rana, P.; Korhonen, L.; Gautam, B.; Tokola, T. Effect of field plot location on estimating tropical forest above ground biomass in Nepal using airborne laser scanning data. ISPRS J. Photogramm. Remote Sens. 2014, 94, 55–62. [Google Scholar] [CrossRef]
- Dube, T.; Mutanga, O. Evaluating the utility of the medium-spatial resolution Landsat 8 multi-spectral sensor in quantifying aboveground biomass in Umgeni catchment, South Africa. ISPRS J. Photogramm. Remote Sens. 2015, 101, 36–46. [Google Scholar] [CrossRef]
- Mathieu, R.; Naidoo, L.; Cho, M.A.; Leblon, B.; Main, R.; Wessels, K.; Asner, G.P.; Buckely, J.; Aardt, J.V.; Erasmus, B.F.N.; et al. Toward structural assessment of semi-arid African savannahs and woodlands: The potential of multitemporal polarimetric RADARSAT-2 fine beam images. Remote Sens. Environ. 2013, 138, 215–231. [Google Scholar] [CrossRef]
- Karlson, M.; Ostwald, M.; Reese, H.; Sanou, J.; Tankoano, B.; Mattsson, E. Mapping tree canopy cover and aboveground biomass in Sudano-Sahelian Woodlands using Landsat 8 and Random forest. Remote Sens. 2015, 7, 10017–10041. [Google Scholar] [CrossRef]
- Karna, Y.K.; Hussin, Y.A.; Gilani, H.; Bronsveld, M.C.; Murthy, M.S.R.; Qamer, F.M.; Karky, B.S.; Bhattarai, T.; Aigong, X.; Baniya, C.B. Integration of WorldView-2 and airborne LiDAR data for tree species level carbon stock mapping in Kayar Khola watershed, Nepal. Int. J. Appl. Earth Obs. Geoinf. 2015, 38, 280–291. [Google Scholar] [CrossRef]
- FRA/DFRS. Terai Forests of Nepal (2010-2012); Forest Resource Assessment Nepal/Department of Forest Research and Survey: Babarmahal, Kathmandu, Nepal, 2014. [Google Scholar]
- Murthy, M.S.R.; Wesselman, S.; Gilani, H. Multi-Scale Forest Biomass Assessment and Monitoring in the Hindu Kush Himalayan Region: A Geospatial Perspective; International Centre for Integrated Mountain Development (ICIMOD): Kathmandu, Nepal, 2015; pp. 70–82. [Google Scholar]
- Muinonen, E.; Parikka, H.; Pokharel, Y.P.; Shrestha, S.M.; Eerikäinen, K. Utilizing a multi-source forest inventory technique, MODIS data and Landsat TM images in the production of forest cover and volume maps for the Terai Physiographic Zone in Nepal. Remote Sens. 2012, 4, 3920–3947. [Google Scholar] [CrossRef]
- Koju, U.; Zhang, J.; Gilani, H. Exploring multi-scale forest above ground biomass estimation with optical remote sensing imageries. IOP Conf. Ser. Earth Environ. Sci. 2017, 57, 012011. [Google Scholar] [CrossRef] [Green Version]
- Pahlevan, N.; Schott, J.R. Leveraging EO-1 to evaluate capability of new generation of Landsat sensors for Coastal/Inland water studies. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 360–374. [Google Scholar] [CrossRef]
- Irons, J.R.; Dwyer, J.L.; Barsi, J.A. The next Landsat satellite: The Satellite data continuity mission. Remote Sens. Environ. 2012, 122, 11–21. [Google Scholar] [CrossRef]
- Zhao, P.; Lu, D.; Wang, G.; Wu, C.; Huang, Y.; Yu, S. Examining spectral reflectance saturation in Landsat Imagery and corresponding solution to improve forest aboveground biomass estimation. Remote Sens. 2016, 8, 469. [Google Scholar] [CrossRef]
- Chave, J.; Andalo, C.; Brown, S.; Cairns, M.A.; Chambers, J.Q.; Eamus, D.; Fölster, H.; Fromard, F.; Higuchi, N.; Kira, T.; et al. Tree allometry and improved estimation of carbon stocks and balance of tropical forest. Ecosyst. Ecol. 2005, 145, 87–99. [Google Scholar] [CrossRef] [PubMed]
- ANSAB; FECOFUN; ICIMOD. Forest Carbon Stock Measurement: Guidelines for Measuring Carbon Stocks in Community-Managed Forests; Asia Network for Sustainable Agriculture and Bioresources (ANSAB), International Centre for Integrated Mountain Development (ICIMOD), and Federation of Community Forest Users, Nepal (FECOFUN): Kathmandu, Nepal, 2010. [Google Scholar]
- Chaturvedi, A.N.; Khanna, L.S. Forest Mensuration; International Book Distributors: Dehra Dun, India, 1982. [Google Scholar]
- Dube, T. Primary Productivity of Intertidal Mudflats in the Wadden Sea: A Remote Sensing Method. Master’s Thesis, University of Twente, Enschede, The Netherlands, 2012. [Google Scholar]
- Dube, T.; Mutanga, O.; Elhadi, A.; Ismail, R. Intra-and-inter species biomass prediction in a plantation forest: Testing the utility of high spatial resolution space borne multispectral RapidEye sensor and advance machine learning algorithms. Sensors 2014, 14, 15348–15370. [Google Scholar] [CrossRef] [PubMed]
- Huete, A.R. A soil-adjusted vegetation index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Rouse, J.W., Jr. Monitoring the Vernal Advancement and Retrogra-Dation (Green wave Effect) of Natural Vegetation; NASA/GSFC: Washington, DC, USA, 1974. [Google Scholar]
- Jordan, C.F. Derivation of leaf-area index from quality of light on the forest floor. Ecology 1969, 50, 663–666. [Google Scholar] [CrossRef]
- Qi, J.; Chehbouni, A.; Huete, A.R.; Kerr, Y.H.; Sorooshian, S. A modified soil adjusted vegetation index. Remote Sens. Environ. 1994, 48, 119–126. [Google Scholar] [CrossRef]
- Hunt, E.R., Jr.; Rock, B.N. Detection of changes in leaf water content using near-and middle-infrared reflectances. Remote Sens. Environ. 1989, 30, 43–54. [Google Scholar] [CrossRef]
- Hardisky, M.A.; Klemas, V.; Smart, R.M. The influence of soil salinity, growth form, and leaf moisture on the spectral radiance of Spartina alterniflora canopies. Photogramm. Eng. Remote Sens. 1983, 49, 77–83. [Google Scholar]
- Pinty, B.; Verstraete, M.M. GEMI: A non-linear index to monitor global vegetation from satellites. Plant Ecol. 1992, 101, 15–20. [Google Scholar] [CrossRef]
- Roujean, J.L.; Breon, F.M. Estimating PAR absorbed by vegetation from bidirectional reflectance measurements. Remote Sens. Environ. 1995, 51, 375–384. [Google Scholar] [CrossRef]
- R Development Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2015. [Google Scholar]
- Davison, A.C.; Hinkley, D.V. Bootstrap Methods and Their Applications; Cambridge University Press: Cambridge, UK, 1997; ISBN 0-521-57391-2. [Google Scholar]
- Faraway, J.J. Practical Regression and ANOVA Using R; University of Michigan: Ann Arbor, MI, USA, 2002. [Google Scholar]
- Kuhn, M. Building Predictive Models in R Using the caret Package. J. Stat. Softw. 2008, 28, 1–26. [Google Scholar] [CrossRef]
- Liaw, A.; Matthew, W. Classification and regression by randomforest. R News 2002, 2, 18–22. [Google Scholar]
- Fassnacht, F.E.; Hartig, F.; Latifi, H.; Berger, C.; Hernández, J.; Corvalán, P.; Koch, B. Importance of sample size, data type and prediction method for remote sensing-based estimations of aboveground forest biomass. Remote Sens. Environ. 2014, 154, 102–114. [Google Scholar] [CrossRef]
- Dube, T.; Mutanga, O. Investigating the robustness of the newly Landsat-8 Operational Land Imager derived texture metrics in estimating plantation forest aboveground biomass in resource constrained areas. ISPRS J. Photogramm. Remote Sens. 2015, 108, 12–32. [Google Scholar] [CrossRef]
- Peat, J.; Barton, B. Medical Statistics: A Guide to Data Analysis and Critical Appraisal; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Öztuna, D.; Elhan, A.H.; Tüccar, E. Investigation of four different normality tests in terms of type 1 error rate and power under different distributions. Turkish J. Med. Sci. 2006, 36, 171–176. [Google Scholar]
- Dye, M.; Mutanga, O.; Ismail, R. Examining the utility of random forest and AISA Eagle hyperspectral image data to predict Pinus patula age in KwaZulu-Natal, South Africa. Geocarto Int. 2011, 26, 275–289. [Google Scholar] [CrossRef]
- Ismail, R.; Mutanga, O. A comparison of regression ensembles: Predicting Sirex noctilio induced water stress in Pinus patula forest of KwaZulu-Natal, South Africa. Int. J. App. Earth Obs. Geoinf. 2010, 12, S45–S51. [Google Scholar] [CrossRef]
- Prasad, A.M.; Iverson, L.R.; Liaw, A. Newer Classification and Regression Tree Techniques: Bagging and Random Forests for Ecological Prediction. Ecosystems 2006, 9, 181–199. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Ozcift, A. Random forest ensemble classifier trained with data resampling strategy to improve cardiac arrhythmia diagnosis. Comput. Biol. Med. 2011, 41, 265–271. [Google Scholar] [CrossRef] [PubMed]
- Palmer, D.S.; O’Boyle, N.M.; Glen, R.C.; Mitchell, J.B.O. Random forest model to predict aqueous solubility. J. Chem. Inf. Model. 2007, 47, 150–158. [Google Scholar] [CrossRef] [PubMed]
- Probst, P.; Boulesteix, A.L. To tune or not to tune the number of trees in random forest. J. Mach. Learn. Res. 2018, 18, 1–18. [Google Scholar]
- Scornet, E.; Biau, G.; Vert, J.P. Consistency of random forests. Ann. Stat. 2015, 43, 1716–1741. [Google Scholar] [CrossRef] [Green Version]
- Genuer, R.; Poggi, J.M.; Tuleau-Malot, C. Variable selection using random forests. Pattern Recognit. Lett. 2010, 31, 2225–2236. [Google Scholar] [CrossRef] [Green Version]
- Steininger, M.K. Satellite estimation of tropical secondary forest above-ground biomass: Data from Brazil and Bolivia. Int. J. Remote Sens. 2000, 21, 1139–1157. [Google Scholar] [CrossRef] [Green Version]
- Lu, D. The potential and challenges of remote sensing-based biomass estimation. Int. J. Remote Sens. 2006, 27, 1297–1328. [Google Scholar] [CrossRef]
- El-Askary, H.; Abd El-Mawla, S.H.; Li, J.; El-Hattab, M.M.; El-Raey, M. Change detection of coral reef habitat using Landsat-5 TM, Landsat 7 ETM+ and Landsat 8 OLI data in the Red Sea (Hurghada, Egypt). Int. J. Remote Sens. 2014, 35, 2327–2346. [Google Scholar] [CrossRef]
- Liu, K.; Wang, J.; Zeng, W.; Song, J. Comparison and evaluation of three models for estimating forest above ground biomass using TM and GLAS data. Remote Sens. 2017, 9, 341. [Google Scholar] [CrossRef]
- Sadeghi, Y.; St-Onge, B.; Leblon, B.; Prieur, J.F.; Simard, M. Mapping boreal forest biomass from a SRTM and TanDEM-X based on canopy height model and Landsat spectral indices. Int. J. Appl. Earth Obs. Geoinf. 2018, 68, 202–213. [Google Scholar] [CrossRef]
- Latifi, H.; Nothdurft, A.; Koch, B. Non-parametric prediction and mapping of standing timber volume and biomass in a temperate forest: Application of multiple optical/LiDAR-derived predictors. Forestry 2010, 83, 395–407. [Google Scholar] [CrossRef]
- Kuhn, M.; Johnson, K. Applied Predictive Modeling; Springer: New York, NY, USA, 2013. [Google Scholar]
- Biau, G.; Scornet, E. A random forest guided tour. Test 2016, 25, 197–227. [Google Scholar] [CrossRef]
- Verikas, A.; Gelzinis, A.; Bacauskiene, M. Mining data with random forests: A survey and results of new tests. Pattern Recognit. 2011, 44, 330–349. [Google Scholar] [CrossRef]
- Oshiro, T.M.; Perez, P.S.; Baranauskas, J.A. How many trees in a random forest. In International Workshop on Machine Learning and Data Mining in Pattern Recognition; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Grömping, U. Variable importance assessment in regression: Linear regression versus random forest. Am. Stat. 2009, 63, 308–319. [Google Scholar] [CrossRef]
- Tyralis, H.; Papacharalampous, G. Variable Selection in Time Series Forecasting Using Random Forests. Algorithms 2017, 10, 114. [Google Scholar] [CrossRef]
- Adam, E.M.; Mutanga, O.; Rugege, D.; Ismail, R. Discriminating the papyrus vegetation (Cyperus papyrus L.) and its co-existent species using random forest and hyperspectral data resampled to HYMAP. Int. J. Remote Sens. 2012, 33, 552–569. [Google Scholar] [CrossRef]
- Chen, J.M. Evaluation of Vegetation Indices and a Modified Simple Ratio for Boreal Applications. Can. J. Remote Sens. 1996, 22, 229–242. [Google Scholar] [CrossRef]
- Ojoyi, M.; Mutanga, O.; Odindi, J.; Abdel-Rahman, E.M. Application of topo-edaphic factors and remotely sensed vegetation indices to enhance biomass estimation in a heterogeneous landscape in the Eastern Arc Mountains of Tanzania. Geocarto Int. 2016, 31, 1–21. [Google Scholar] [CrossRef]
- Mutanga, O.; Skidmore, A.K. Narrow band vegetation indices overcome the saturation problem in biomass estimation. Int. J. Remote Sens. 2004, 25, 3999–4014. [Google Scholar] [CrossRef]
- Shao, Z.; Zhang, L. Estimating forest aboveground biomass by combining optical and SAR data: A case study in Genhe, Inner Mongolia, China. Sensors 2016, 16, 834. [Google Scholar] [CrossRef] [PubMed]
- Adam, E.M.; Mutanga, O.; Abdel-Rahman, E.M.; Ismail, R. Estimating standing biomass in papyrus (Cyperus papyrus L.) swamp: Exploratory of in situ hyperspectral indices and random forest regression. Int. J. Remote Sens. 2014, 35, 693–714. [Google Scholar] [CrossRef]
- Lu, D.; Mausel, P.; Brondızio, E.; Moran, E. Relationships between forest stand parameters and Landsat TM spectral responses in the Brazilian Amazon Basin. For. Ecol. Manag. 2004, 198, 149–167. [Google Scholar] [CrossRef] [Green Version]
- Kumar, R.; Gupta, S.R.; Singh, S.; Patil, P.; Dhadhwal, V.K. Spatial distribution of Forest biomass using remote sensing and regression models in Northern Haryana, India. Int. J. Ecol. Environ. Sci. 2011, 37, 37–47. [Google Scholar]
- Zheng, D.; Rademacher, J.; Chen, J.; Crow, T.; Bresee, M.; Le Moine, J.; Ryu, S.R. Estimating aboveground biomass using Landsat 7 ETM+ data across a managed landscape in northern Wisconsin, USA. Remote Sens. Environ. 2004, 93, 402–411. [Google Scholar] [CrossRef]
- Foody, G.M.; Cutler, M.E.; Mcmorrow, J.; Pelz, D.; Tangki, H.; Boyd, D.S.; Douglas, I. Mapping the biomass of Bornean tropical rain forest from remotely sensed data. Global Ecology and Biogeography 2001, 10, 379–387. [Google Scholar] [CrossRef]
- Rahman, M.M.; Csaplovics, E.; Koch, B. An efficient regression strategy for extracting forest biomass information from satellite sensor data. Int. J. Remote Sens. 2005, 26, 1511–1519. [Google Scholar] [CrossRef]
- Kumar, L.; Mutanga, O. Remote Sensing of Above-Ground Biomass. Remote Sens. 2017, 9, 935. [Google Scholar] [CrossRef]





| Data Type | Model | Input Variables |
|---|---|---|
| Image spectral information (ISI) | MLR | band 2 (BLUE), band 3 (GREEN), band 4 (RED), band 5 (NIR), band 6 (SWIR1), band 7 (SWIR2) |
| Vegetation indices (VIs) | MLR | DVI, GEMI, GNDVI, MSAVI2, MSI, NDII, NDVI, OSAVI, RDVI, MSR, SAVI, SR, TVI, and IPVI |
| ISI + VIs | MLR/RF | ISI + DVI, GEMI, GNDVI, MSAVI2, MSI, NDII, NDVI, OSAVI, RDVI, MSR, SAVI, SR, TVI, and IPVI |
| Most important variables | RF | OSAVI, NDVI, SR, MSR, band 6, MSI, NDII, MSAVI2, RDVI, GEMI, band 7, SAVI , band 2, band 4, and band 1 |
| Most importantvariables | MLR | band 5 and SR (pooled data), SR and MSI (VIs), and band 1, band 5, and band 7 |
| Band reflectance used | Blue, Red, SWIR1, SWIR2 | |
|---|---|---|
| Vegetation indices | Formula | References |
| Optimized soil-adjusted vegetation index (OSAVI) | [(NIR − RED) / (NIR + RED + L)] × (1 + L), where L = 0.16 and is the soil brightness correction factor | [27] |
| Normalized difference vegetation index (NDVI) | (NIR − RED) / (NIR + RED) | [28] |
| Simple ratio (SR) | NIR/RED | [29] |
| Modified simple ratio (MSR) | (NIR / RED) − 1 / √((NIR / RED)) + 1 | [30] |
| Moisture stress index (MSI) | ꝭ1599 µm / ꝭ819 µm, where ꝭ = wavelength, Band 5 = 819 µm, Band 6 µm = 1599 | [31] |
| Normalized difference infrared index (NDII) | (ꝭ819 µm − ꝭ1649 µm) / (ꝭ819 µm + ꝭ1649 µm), where Band 5 = 819 µm, Band 6 = 1599 µm | [32] |
| Global environmental monitoring index (GEMI) | n × (1 − 0.25 n) − [(RED − 0.125) / (1 − RED), where n = [2 × (NIR2 − RED2) + 1.5 × NIR + 0.5 × RED] / (NIR + RED + 0.5) | [33] |
| Second modified soil-adjusted vegetation index (MSAVI2) | 1/2 × ((NIR + 1) − sqrt ((2 × NIR+ 1)2 − 8(NIR − RED))) | [30] |
| Renormalized difference vegetation index (RDVI) | (NDVI × DVI)0.5 | [34] |
| Soil-adjusted vegetation index (SAVI) | (NIR − RED) / (NIR + RED + L) × (1 + L), where L = 0.5 | [27] |
| No. | Name of Forest | Total No. of Plots | Min(t ha−1) | Max(t ha−1) | Mean(t ha−1) | Standard Deviation |
|---|---|---|---|---|---|---|
| 1 | Ratomate Deurali BZCF | 17 | 35.25 | 115.95 | 115.87 | 33.66 |
| 2 | Jyamire BZCF | 30 | 34.75 | 304.19 | 166.81 | 88.60 |
| 3 | Radha Krishna BZCF | 59 | 105.40 | 230.72 | 174.91 | 35.51 |
| 4 | Janahit BZCF | 30 | 96.95 | 286.56 | 172.18 | 47.32 |
| 5 | Shrijana BZCF | 21 | 30.34 | 200.22 | 117.94 | 56.33 |
| 6 | Mushaharnimae BZCF | 16 | 90.95 | 210.48 | 170.52 | 40.26 |
| Cross-Validation | |||||
|---|---|---|---|---|---|
| Final Variable Inputs in the Model | R2 | Adj. R2 | RMSE (t ha−1) | relRMSE (%) | RMSE-CV |
| Band 1, band 5, and band 7 | 0.41 | 0.39 | 43.85 | 27.42 | 0.27 |
| SR and MSI | 0.57 | 0.56 | 37.23 | 23.08 | 0.23 |
| Band 5 and SR | 0.56 | 0.56 | 37.01 | 23.05 | 0.23 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pandit, S.; Tsuyuki, S.; Dube, T. Landscape-Scale Aboveground Biomass Estimation in Buffer Zone Community Forests of Central Nepal: Coupling In Situ Measurements with Landsat 8 Satellite Data. Remote Sens. 2018, 10, 1848. https://doi.org/10.3390/rs10111848
Pandit S, Tsuyuki S, Dube T. Landscape-Scale Aboveground Biomass Estimation in Buffer Zone Community Forests of Central Nepal: Coupling In Situ Measurements with Landsat 8 Satellite Data. Remote Sensing. 2018; 10(11):1848. https://doi.org/10.3390/rs10111848
Chicago/Turabian StylePandit, Santa, Satoshi Tsuyuki, and Timothy Dube. 2018. "Landscape-Scale Aboveground Biomass Estimation in Buffer Zone Community Forests of Central Nepal: Coupling In Situ Measurements with Landsat 8 Satellite Data" Remote Sensing 10, no. 11: 1848. https://doi.org/10.3390/rs10111848
APA StylePandit, S., Tsuyuki, S., & Dube, T. (2018). Landscape-Scale Aboveground Biomass Estimation in Buffer Zone Community Forests of Central Nepal: Coupling In Situ Measurements with Landsat 8 Satellite Data. Remote Sensing, 10(11), 1848. https://doi.org/10.3390/rs10111848