Ultrahigh Resolution Scatterometer Winds near Hawaii
Abstract
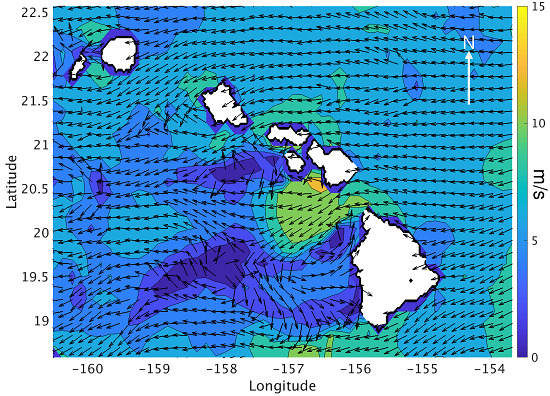
:1. Introduction
2. Scatterometer UHR Wind Estimates in the Lee of the Big Island
3. Comparison of Scatterometer Measured and Model Predicted
3.1. QuikSCAT versus Model Predicted
3.2. ASCAT versus Model Predicted
3.3. Summary
4. Nudging Field and Median Filter Window Size
5. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ulaby, F.T.; Long, D.G. Microwave Radar and Radiometric Remote Sensing; The University of Michigan Press: Ann Arbor, MI, USA, 2014. [Google Scholar]
- Long, D.G. Polar Applications of Spaceborne Scatterometers. IEEE J. Sel. Top. Appl. Earth Observ. 2017, 10, 2307–2320. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lindell, D.B.; Long, D.G. High-Resolution Soil Moisture Retrieval with ASCAT. IEEE Geosci. Remote Sens. Lett. 2016, 13, 972–976. [Google Scholar] [CrossRef]
- Lindell, D.; Long, D. Multiyear Arctic ice classification using ASCAT and SSMIS. Remote Sens. 2016, 8, 294. [Google Scholar] [CrossRef] [Green Version]
- Chang, P.S.; Jelenak, Z.; Sienkiewicz, J.M.; Knabb, R.; Brennan, M.J.; Long, D.G. Operational use and impact of satellite remotely sensed ocean surface vector winds in the marine warning and forecasting environment. Oceanography 2009, 22, 194–207. [Google Scholar] [CrossRef] [Green Version]
- Wentz, F.J.; Ricciardulli, L.; Rodriguez, E.; Stiles, B.W.; Bourassa, M.A.; Long, D.G.; Hoffman, R.N.; Stoffelen, A.; Verhoef, A.; O’Neill, L.W.; et al. Evaluating and extending the ocean wind climate data record. IEEE J. Sel. Top. Appl. Earth Observ. 2017, 10, 2165–2185. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Owen, M.P.; Long, D.G. Land Contamination Compensation for QuikSCAT Near-Coastal Wind Retrieval. IEEE Trans. Geoscie. Remote Sens. 2009, 47, 839–850. [Google Scholar] [CrossRef]
- Physical Oceanography Distributed Active Archive Center (PO.DAAC). Seawind’s User Guide; Rev. 3.0; Physical Oceanography Distributed Active Archive Center: Pasadena, CA, USA, 2006. [Google Scholar]
- Hersbach, H.; Stoffelen, A.; de Haan, S. An improved C-band scatterometer ocean geophysical model function: CMOD5. J. Geophys. Res. Oceans 2007, 112. [Google Scholar] [CrossRef]
- Naderi, F.M.; Freilich, M.H.; Long, D.G. Spaceborne radar measurement of wind velocity over the ocean-an overview of the NSCAT scatterometer system. Proc. IEEE 1991, 79, 850–866. [Google Scholar] [CrossRef]
- Shaffer, S.J.; Dunbar, R.S.; Hsiao, S.V.; Long, D.G. A median-filter-based ambiguity removal algorithm for NSCAT. IEEE Trans. Geosci. Remote Sens. 1991, 29, 167–174. [Google Scholar] [CrossRef] [Green Version]
- Schultz, H. A circular median filter approach for resolving directional ambiguities in wind fields retrieved from spaceborne scatterometer data. J. Geophys. Res. 1990, 95, 5291–5303. [Google Scholar] [CrossRef]
- Xie, S.P.; Liu, W.T.; Liu, Q.; Nonaka, M. Far-reaching effects of the Hawaiian islands on the Pacific Ocean-atmosphere system. Science 2001, 292, 2057–2060. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sakamoto, T.T.; Sumi, A.; Emori, S.; Nishimura, T.; Hasumi, H.; Suzuki, T.; Kimoto, M. Far-reaching effects of the Hawaiian Islands in the CCSR/NIES/FRCGC high-resolution climate model. Geophys. Res. Lett. 2004, 12. [Google Scholar] [CrossRef]
- Kilpatrick, T.; Xie, S.; Tokinaga, H.; Long, D.; Hutchings, N. Systematic scatterometer wind errors near coastal mountains. Earth Space Sci. 2019, 6, 1900–1924. [Google Scholar] [CrossRef] [PubMed]
- Nickerson, E.C.; Dias, M.A. On the existence of atmospheric vortices downwind of Hawaii during the HAMEC project. J. Appl. Meteorol. 1981, 20, 868–873. [Google Scholar] [CrossRef] [Green Version]
- Smith, R.B.; Grubišić, V. Aerial observations of Hawaii’s wake. J. Atmos. Sci. 1993, 50, 3728–3750. [Google Scholar] [CrossRef] [Green Version]
- Patzert, W.C. Eddies in Hawaiian Waters; Technical report; Hawaii Inst of Geophysics: Honolulu, HI, USA, 1969. [Google Scholar]
- Zhang, C.; Yuqing Wang, A.L.; Hamilton, K. Configuration and evaluation of the WRF model for the study of Hawaiian regional climate. Mon. Weather Rev. 2012, 140, 3259–3277. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, J. Evaluation of ISS-RapidScat wind vectors using buoys and ASCAT data. Remote Sens. 2018, 10, 648. [Google Scholar] [CrossRef] [Green Version]
- Asia-Pacific Data Research Center. 2019. Available online: http://apdrc.soest.hawaii.edu/ (accessed on 30 January 2020).
- Zhang, C.; Wang, Y.; Hamilton, K.; Lauer, A. Dynamical downscaling of the climate for the Hawaiian Islands. Part I: Present day. J. Clim. 2016, 29, 3027–3048. [Google Scholar] [CrossRef] [Green Version]
- Lindsley, R.; Long, D.G. Enhanced-Resolution Reconstruction of ASCAT Backscatter Measurements. IEEE Trans. Geosci. Remote Sens. 2016, 54, 2589–2601. [Google Scholar] [CrossRef]
- Williams, B.A.; Long, D.G. A reconstruction approach to scatterometer wind vector field retrieval. IEEE Trans. Geosci. Remote Sens. 2011, 49, 1850–1864. [Google Scholar] [CrossRef]
- Plagge, A.; Vandemark, D.C.; Long, D.G. Coastal validation of ultra-high resolution wind vector retrieval from QuikSCAT in the Gulf of Maine. IEEE Geosci. Remote Sens. Lett. 2009, 6, 413–417. [Google Scholar] [CrossRef]
- Williams, B.A.; Owen, M.P.; Long, D.G. The ultra high resolution QuikSCAT product. In Proceedings of the 2009 IEEE Radar Conference, Pasadena, CA, USA, 4–8 May 2009; pp. 1–6. [Google Scholar] [CrossRef] [Green Version]
- Williams, B.A.; Long, D.G. Estimation of Hurricane Winds from SeaWinds at Ultra High Resolution. IEEE Trans. Geosci. Remote Sens. 2008, 46, 2924–2935. [Google Scholar] [CrossRef] [Green Version]
- Owen, M.P.; Long, D.G. Simultaneous Wind and Rain Estimation for QuikSCAT at Ultra-High Resolution. IEEE Trans. Geosci. Remote Sens. 2011, 49, 1865–1878. [Google Scholar] [CrossRef]
- Owen, M.P.; Long, D.G. Prior Selection for QuikSCAT Ultra-High Resolution Wind and Rain Retrieval. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1555–1567. [Google Scholar] [CrossRef]
- Hutchings, N.; Long, D.G. Improved Ultrahigh-Resolution Wind Retrieval for RapidScat. IEEE Trans. Geosci. Remote Sens. 2018, 57, 3370–3379. [Google Scholar] [CrossRef]
- Lindsley, R.; Blodgett, J.R.; Long, D.G. Analysis and Validation of High-Resolution Wind from ASCAT. IEEE Trans. Geosci. Remote Sens. 2016, 54, 5699–5711. [Google Scholar] [CrossRef]
- Lindsley, R.D. Enhanced-Resolution Processing and Applications of the ASCAT Scatterometer. Ph.D. Thesis, Brigham Young University, Provo, UT, USA, 2015. [Google Scholar]
- Freilich, M.H.; Dunbar, R.S. The accuracy of the NSCAT 1 vector winds: Comparisons with National Data Buoy Center buoys. J. Geophys. Res. 1999, 104, 11232–11246. [Google Scholar] [CrossRef]
- Liu, W.T.; Tang, W. Equivalent Neutral Wind; Jet Propulsion Laboratory Publication: Pasadena, CA, USA, 1996; pp. 96–117. [Google Scholar]










© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hutchings, N.; Kilpatrick, T.; Long, D.G. Ultrahigh Resolution Scatterometer Winds near Hawaii. Remote Sens. 2020, 12, 564. https://doi.org/10.3390/rs12030564
Hutchings N, Kilpatrick T, Long DG. Ultrahigh Resolution Scatterometer Winds near Hawaii. Remote Sensing. 2020; 12(3):564. https://doi.org/10.3390/rs12030564
Chicago/Turabian StyleHutchings, Nolan, Thomas Kilpatrick, and David G. Long. 2020. "Ultrahigh Resolution Scatterometer Winds near Hawaii" Remote Sensing 12, no. 3: 564. https://doi.org/10.3390/rs12030564
APA StyleHutchings, N., Kilpatrick, T., & Long, D. G. (2020). Ultrahigh Resolution Scatterometer Winds near Hawaii. Remote Sensing, 12(3), 564. https://doi.org/10.3390/rs12030564