Introduction

Optical bound state in the continuum (BIC) is a highly localized optical mode trapped in a structure in a lossless regime regardless of the presence of a leakage channel due to the radiation feature dictated by the dispersion spectrum1,2,3,4,5,6. A BIC mode occurs at a certain special point of the dispersion diagram as a result of the destructive interference in the host structure that suppresses the radiative mode. Hence, light is trapped within the structure while otherwise, it should leak out. The unique feature of BIC is its very narrow resonance, in other words, an extremely high quality (Q) factor, theoretically reaching infinitely high numbers in the case of an ideal structure with an infinite lattice, absence of material absorption, and structural defects. In a realistic experimental system with a finite number of periodic elements and such imperfections as surface roughness and material loss, a BIC is called a quasi-BIC, which possesses a high but finite Q-factor. Intentionally introduced perturbation of structures also allows for the control of the Q-factor. High Q-factors and highly confined electric fields of BIC modes are attractive for various potential applications, such as lasing7,8, enhancement of the second- and third-harmonic generation9,10,11,12,13,14,15, light modulation16, biochemical sensing17,18,19,20,21,22,23,24,25,26,27 and imaging28, upconversion29.

Up to present, BIC modes have been observed in various periodic systems, including arrays of dielectric pillars2 and grating structures30, metasurfaces in various designs7,8,9,10,11,12,13,14,15,16,17,18,19,20,23,25,31,32,33, as well as aperiodic systems including a single resonator22, anisotropic waveguides34 and interfaces35. Furthermore, photonic crystal (PhC) structures are other settings where BIC modes are conventionally observed3,17,21,28,29. A photonic crystal is a periodic arrangement of dielectric or metallic elements with a period typically smaller than the wavelength of light. A characteristic feature of a PhC is the presence of a wavelength interval where light propagation is prohibited, referred to as a photonic bandgap (or a stop band)36. A two-dimensional photonic crystal (2DPhC) is typically an air hole array in a dielectric matrix or an array of dielectric discs or pillars erected on a substrate in an air background. Among other configurations, quasi-BIC modes in 2DPhCs have been observed in a square-lattice air hole array in a silicon nitride slab3,17, flower pattern in a Si slab37, and Si discs in square lattice structures38.

Two major types of BIC modes are supported on PhC structures: symmetry-protected (SP) BICs and accidental BICs4. SP-BICs exist at the Γ point of the dispersion diagram and do not possess in-plane wavevector components. On the other hand, accidental BICs, which are also referred to as Fredrich-Wintgen bound states in the continuum (FW-BIC), possess a non-zero in-plane wavevector and thus are propagating along the structure. FW-BICs have been observed in 2DPhC systems3,21,28,29,37. However, apart from these two major types, a unique type of a BIC surface mode has been predicted, which is supported at the edge of a truncated 2DPhC. To host such a mode, the terminating row of dielectric pillars should have a different diameter from the rest of the pillars39,40. Depending on the pillar diameter, either BIC modes that exist above light line or surface modes below the light line can be supported. The predicted BIC modes are Bloch surface-localized eigenstates, discrete states supported at the edge periodic arrangement, such as photonic crystals and gratings, which exist inside the free space continuum above the light line. While such modes leak into free space, under certain conditions, the incoming and back-reflected leakage radiation interfere destructively and result in no leakage. Initially, the predicted BICs are called Bloch BIC. Other Bloch BICs have been studied for 1D gratings41,42. In order to distinguish from these Bloch BIC on 1D gratings and surface modes at the edge of 2DPhC, we refer the current BIC under investigation as “edge BICs” in this article.

An edge BIC mode is also categorized as a Fabry-Pérot (FP) type BIC4,5 that is trapped between two reflectors. FP-BICs were theoretically studied for systems where reflectors are an asymmetric ridge with different thickness of waveguide films43 or anisotropic one-dimensional PhC44. Some of them have been experimentally observed for an array of dielectric waveguides where the reflectors are waveguide array and isotropic dielectric media45 and a metasurface made of gold nanoparticles, where a gold film above the metasurface is used as a reflector16. In the case of FP-BICs supported in 2DPhCs, the terminating layer of larger Si pillars is sandwiched between a pair of reflective interfaces, namely, the interface with air and that of 2DPhC with a photonic bandgap as the reflector39,40. Here, the air forms a leakage channel. FP-BIC modes with an electric field parallel to the pillars (TM polarization) exist within the photonic bandgap of the 2DPhC. As a result, the BIC mode propagates along the terminating array of dielectric pillars, being highly localized in their vicinity. Here we also stress that FP-BICs exist within the photonic bandgap above the light line, distinguishing them from FW-BICs, which are associated with one of the propagating modes of the 2DPhC outside the photonic bandgap3,21,28,29,37.

Here, we experimentally demonstrate the special type of Fabry-Pérot bound states in the continuum for near-infrared wavelengths supported at the edge of a two-dimensional photonic crystal patch. The 2DPhC is composed of Si pillars in a square lattice arrangement. One edge of 2DPhC structures is truncated by an array of Si pillars whose diameter is bigger than the rest of the pillars, as shown in Fig. 1a – c. We refer to this particular quasi-BIC mode as edge BIC, which distinguishes from other types of observed FP-BICs45 and surface BIC supported at the interface of anisotropic media35. The quality factor and resonance wavelength of the edge BIC modes are changed by a slight change in the terminating layer diameter by even a few nanometers. To the best of our knowledge, this is the first report on the observation of edge BICs on truncated 2DPhCs. We also show that a slight change of the dielectric environment by a nanometer-thick dielectric layer deposited around Si pillars improves the Q-factor from 237 to 396 and shifts the quasi-BIC’s resonance wavelength with 1.12 nm for every nanometer of the film thickness. This shows the option of the post-fabrication tuning of edge BIC modes and a strong potential for sensing applications in the detection of biomarkers.

Fig. 1: Truncated two-dimensional (2D) photonic crystal (PhC) structure, supporting edge bound state in the continuum (BIC).
figure 1

a Top and (b) birds-eye-view of scanning electron microscope (SEM) images of Si pillar PhCs and ridge waveguides after the deposition of 7.3 nm thick alumina film. The white dashed box corresponds to the inset of SEM image (black dashed box). Si pillars with 1.5 μm height lie on approximately 0.9 μm SiO2 pillars. c The design of Si pillar PhC system and Si ridge waveguides on silicon on insulator (SOI) wafer (top view). The PhC structures under consideration have a lattice constant (period) of a = 600 nm, diameter Dt = 260 nm for the terminating layer and D = 160 nm for the rest of Si pillars, height H = 1.5 μm. The number of periods along the x- and y-axis is Nx = 33 and Ny = 15, including the terminating layer, giving the Si pillar PhC area of 19.8  × 9.0 μm. d Schematic illustration of the experimental setup for end-fire coupling to measure transmission spectra through 2DPhC (side view). Coupling and out-coupling of light is done by polarization-maintaining (PM) fibers. The width of both Si ridge waveguides is w = 1.0 μm, and their lengths are approximately 4 mm long for both input and out-coupling parts.

Full size image

Results

Numerical simulation

The 2DPhC structures under consideration have a lattice constant (period) of a = 600 nm, diameter Dt = 270 nm for the terminating layer, and D = 160 nm for the rest of Si pillars with height H = 1.5 μm. The Si pillars stand on top of SiO2 pillars with 0.9 μm height created by under etch of SiO2 layer (Fig. 1b and Supplementary Fig. S1) in order to make the mode confined within Si pillars due to effective refractive index contrast between Si pillars and SiO2 pillars. Without the under etch of SiO2, the quasi-BIC mode significantly leaks into SiO2 layer and consequently, the transmission peak cannot be observed (Supplementary Figs. S2 and S3). The etch depth of 0.9 μm is chosen to suppress the leakage while not damaging the Si pillars themselves (Supplementary Fig. S4). The fabricated photonic crystal structure has Nx = 33 and Ny = 15 periods along x- and y-axis, respectively, covering 19.8 μm  × 9.0 μm area (Fig. 1c). Note that the number Ny of 2DPhC periods along y-axis needs to be sufficient for the photonic crystal to function as a reflector, and Ny = 5 is enough as was validated in46 (see also Supplementary Fig. S5). The 2DPhC area is in- and out-coupled by a pair of Si ridge waveguides with the same height of H = 1.5 μm and width w = 1.0 μm. These ridge waveguides stretch from the edge of the substrate and are used to inject broadband light into the 2DPhC area and to out-couple the guided modes to the polarization-maintaining (PM) single-mode fibers and further to the spectrometer (Fig. 1d). The 2DPhC and Si ridge waveguides are fabricated on a silicon on insulator (SOI) substrate with 2.0 μm thick silica (SiO2) layer (Materials and methods).

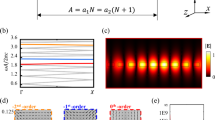
We conducted numerical analysis to elucidate the nature of edge-bound states in the continuum, as shown in Fig. 2. Figure 2a shows the dispersion diagram of 2DPhC with lattice constant a = 600 nm and diameter of Si pillars D = 160 nm in air background. Such 2DPhC lattice has the bandgap extended for ωa/2πc = a/λ = 0.352–0.482, corresponding to λ = 1244–1704 nm. The BIC appears within the photonic bandgap above the light line so that the mode in the terminating layer is reflected from the PhC side and the air semispace in a destructive manner. The edge BIC mode localized in the terminating layer propagates along the Γ-X direction of 2DPhC.

Fig. 2: Simulation of edge-bound states in the continuum (BIC).
figure 2

a Simulated dispersion of two-dimensional photonic crystal (2DPhC) composed of Si pillars in a square lattice arrangement with air background, lattice constant a = 600 nm, diameter of D = 160 nm for transverse magnetic (TM) polarization (Ez parallel to Si pillars). The photonic bandgap extends from ωa/2πc = a/λ = 0.352 to 0.482 (λ = 1244–1704 nm). The position of the observed edge BIC at ωa/2πc = a/λ = 0.421 (λ = 1424 nm, k ~ 0.25) is marked by a red circle above the light line. b Dispersion for the 2DPhC with the terminating layer with Dt = 270 nm in air with the light line. The dashed square corresponds to the parameter space for (c) Quality factor of the leaky surface modes along the dashed red line in b. The inset shows the electric field profile of Ez at A: kx = 0.24, B: kx = 0.26325, and C: kx = 0.28. d Simulated transmission spectra in 3D for three different diameters of terminating Si pillars, Dt = 270 nm (red), 275 nm (green), and 280 nm (blue), respectively. e Ez electric field profile of propagating mode (electric field parallel to Si pillars) through the terminating layer with Si pillar diameter Dt = 270 nm and D = 160 nm for 2DPhC for λ = 1424 nm. The inset shows the enlargement of dashed rectangular, showing one effective wavelength (period) of the edge BIC mode.

Full size image

We also calculated the dispersion diagram for the 2DPhC with the terminating layer of Si pillars with diameter, Dt = 270, as shown in Fig. 2b. We locate a guided surface mode below the light line within the photonic bandgap, which transforms into a leaky mode above the light line (red dashed line in Fig. 2b). This leaky mode is the candidate to become a BIC mode, as predicted in the similar way in ref. 39. To locate the quasi-BIC mode, we analyzed the Q-factor of the leaky mode under question for the range of kx = 0.22–0.30 (Fig. 2)c. A sharp increase of lifetime (Q-factor) that approaches infinity when the surface-parallel wavevector is near kx = 0.26325. At this point B of Fig. 2c, the radiation of resonant mode is suppressed, while at the vicinity of point B (A and C points), fields are intensively leaking into the air.

Figure 2d shows the simulated transmission spectra through the 2DPhC with the terminating layer composed of a row of Si pillars with diameter Dt = 270–280 nm. Note that this wavelength interval λ = 1400–1500 nm is completely within the photonic bandgap (λ = 1244–1704 nm) that does not accept any light waves except for the edge BIC modes guided through the terminating layer. Therefore, we observe the transmission peak in low transmission background. The transmission peak red-shifts as the diameter becomes bigger. Moreover, the full-width at half maximum (FWHM) enlarges from FWHM = 10.2 nm of Dt = 270 nm to FWHM = 11.7 nm and 22.6 nm for Dt = 275 nm and 280 nm, respectively. The corresponding Q-factors degrade from Q = 139 (Dt = 270 nm) to 123 (Dt = 275 nm) and down to 64 (Dt = 280 nm) due to the broadening of the resonance peak. Thus, the diameter Dt can be optimized for the high-Q resonance edge BIC mode.

The field profiles in Fig. 2e exhibit a high concentration of the electric field around the terminating layer, similar to the edge BICs reported in ref. 39. We can also see that the field pattern repeats after approximately four periods of pillars. Thus, the effective wavelength λeff of this mode is λeff ≈ 4a = 2400 nm for the vacuum wavelength of λ = 1424 nm, resulting in the normalized wavevector (in other words effective refractive index of the mode) of N = 1424 nm/2400 nm = 0.593. Note that here N = β/k0 where β is propagation constant and k0 is wavevector in vacuum, k0 = 2π/λ. Since N < 1, this propagating mode exists above the light line of the dispersion spectra and leaks into the air, satisfying the condition of edge BICs. Moreover, kx = βa/2π = k0Na/2π = Na/λ ≈ 0.25, which corresponds to kx = 0.26325 of point B in Fig. 2c and Fig. 5b of ref. 40. The normalized frequency of the edge BIC is ωa/2πc = a/λ = 600 nm/1424 nm = 0.421. This is within the photonic bandgap of the 2DPhC (ωa/2πc = 0.352 – 0.482 in Fig. 2a), also satisfying the condition for supporting edge BICs in 2DPhCs.

Measured transmission spectra

Silicon pillar PhC samples were fabricated by electron beam lithography and dry etching technique on silicon-on-insulator (SOI) wafers, as described in Materials and Methods. Here we stress that without the under etch of SiO2 layer, we were unable to observe narrow transmission peak associated with the edge BICs due to the leakage of mode energy into substrate (see Supplementary Figs. S2 and S3), which may have prevented the demonstration of this edge BIC mode up to present. With the SiO2 pedestal pillars underneath the Si pillars, the BIC modes are more confined within the Si pillars and observable transmission peaks are realized.

Figure 3 a shows measured transmission spectra for the 2DPhC samples (lattice constant a = 600 nm and Si pillar diameter D = 160 nm) in air with different diameters of the pillars in the terminating layer, Dt. We observe a transmission peak at λ = 1424.0 nm for the 2DPhC with Dt = 260 nm, which corresponds to the simulation of Dt = 270 nm case. This discrepancy in the optimal diameter Dt (Fig. 2d) between the simulation and experiment can be attributed to the imperfections in nanofabrication, such as the surface roughness of the pillars’ side walls and rounding of top of pillars (see Supplementary Figs. S1 and S6). The transmission peak red-shifts (normalized frequency decreases as in Fig. 3b) for larger diameter Dt = 264 and 270 nm. The FWHM of the observed resonance of Dt = 260 nm is FWHM = 6.0 nm, which gives a quality factor of Q = λ/FWHM = 237, as summarized in Table 1. For Dt = 264 and 270 nm, the Q-factor decreases to Q = λ/FWHM = 170 and 160, respectively. The shape of resonance deforms for larger Dt, and as a result, the Q-factor degrades too (Fig. 3c), following the tendency observed in simulations.

Fig. 3: Observation of edge-bound states in the continuum (BIC).
figure 3

a Measured normalized transmission spectra through Si pillar photonic crystals (2DPhC) with three different diameters of terminating Si pillars, Dt = 260 nm (red), 264 nm (green), and 270 nm (blue), respectively. The 2DPhC samples have the period a = 600 nm, height H = 1.5 μm height, and D = 160 nm and the termination row of Si pillars with Dt = 260 -- 270 nm. b Normalized frequency, ωa/2πc, and (c) quality factor of quasi-BIC modes for different diameters, Dt.

Full size image
Table 1 Summary of the measured performance of edge bound state in the continuum (BIC) supported on two-dimensional photonic crystal (2DPhC)
Full size table

Tunability and surface sensitivity measurement

Next, we investigate the tuning of the edge BIC resonance by a dielectric nanofilm conformally deposited on the 2DPhC structures with Dt = 260 nm and D = 160 nm. For that, alumina (Al2O3) layers with a refractive index of 1.6147 around 1400–1500 nm wavelengths and thicknesses ta between 2.5 to 7.3 nm are deposited on the sample’s surface by the atomic layer deposition (ALD) technique (Materials and methods). Transmission measurements help to evaluate edge BIC’s resonance tunability and surface sensitivity. Transmission spectra for samples with extra ta = 2.5 nm, 4.7 nm, and 7.3 nm thick alumina coatings are shown in Fig. 4a. As summarized in Table 1, the transmission peak corresponding to the edge BIC mode red-shifts from 1424.0 nm to 1432.2 nm with a corresponding normalized frequency decrease (Fig. 4b) due to the increase of the local refractive index around Si pillars. For ta = 2.5 nm, the transmission peak with FWHM = 3.6 nm shifts to 1426.6 nm from the original position at 1424.0 nm with the reference sample without the alumina layer, giving increased Q = λ/FWHM = 396, as plotted in Fig. 4c. For ta = 4.7 nm and 7.3 nm, the Q-factor significantly drops to Q = λ/FWHM = 270 and 247, respectively. This shows that we can realize fine post-tuning of the resonance and even improve the Q-factor from Q = 237 to 396 by depositing the dielectric nanofilm with the thickness of ta = 2.5 nm. This is a remarkable improvement of the Q-factor by 67 % compared with the reference structure without the alumina layer.

Fig. 4: Surface sensitivity and tunability of quasi-bound state in the continuum (BIC).
figure 4

a Transmission spectra of two-dimensional (2D) Si pillar photonic crystals (PhCs) with different alumina thicknesses, ta = 0 nm as reference (Ref. red), 2.5 nm (blue), 4.7 nm (gray), and 7.3 (black), for Dt = 260 nm and D = 160 nm. The inset shows the surface sensitivity Ss as the resulting resonance shift in wavelength for the thickness of alumina layers deposited on the samples. b Resonance in normalized frequency, ωa/2πc, and (c) quality factor in terms of deposited alumina film thickness, ta.

Full size image

The pronounced wavelength shift induced by the nanometer-thick dielectric coating can be used for surface refractometric sensing to detect biomarkers. Surface sensitivity, a measure of wavelength shift, Δλ, for the thickness of the analyte layer, ta is defined by48,49,50,51

$${S}_{s}=\frac{\Delta \lambda [nm]}{{t}_{a}[nm]}.$$
(1)

In the case of refractometric sensing where analyte molecules form nanometer-thick film on sensor surface, the surface sensitivity is relevant. The resonance shift by an alumina nanofilm in linear fit gives a comfortable 1.12 nm variation with every nanometer of a binding layer thickness as shown in the inset of Fig. 4a. The observed surface sensitivity of 1.12 nm edge BICs shift for every nanometer thickness is comparable to 1.24–1.40 nm/nm sensitivity of guided-mode resonances supported in Si high-contrast grating structures with alumina layer as model analyte in air background49,50. To improve the surface sensitivity, the parameters of 2DPhC and terminating layer, especially their diameters, should be optimized to maximize the overlap of field and analyte48.

Apart from the implication of potential applications for biosensing, the 2DPhC system supporting edge BICs may also find applications in temperature sensors and all-optical modulators for optical signals. The former application is due to the alteration of the ambient medium properties with temperature. The latter can be granted by the significant modulation strength of a system with powerful radiation. Recently, pronounced optical modulation by low fluence was demonstrated for Si metasurfaces that support collective modes such as guide mode resonances with comparable Q-factor ( ~170) for similar wavelengths (λ ~ 1380 nm)52. We anticipate that the edge BIC supported on Si-based 2DPhC and waveguides can be modulated by optical pulses at telecommunication wavelengths in a similar manner.

Discussion

A nanometer-thick oxide layer can shift the edge BIC resonance and improve its Q-factor. This suggests that the edge BIC resonance can be tuned by thin films conformally deposited by ALD as the post-fabrication tuning option. The ALD technique offers precise control of layer thickness and is advantageous for tuning edge BIC resonance. The maximum observed Q-factor of 396 with a 2.5 nm thick alumina layer increased from Q = 237 of the as-fabricated PhC is comparable to the reported numbers of Si-based metasurfaces supporting symmetry-protected BIC for the same wavelength region10,11,23. Further improvement of the Q factor can be realized in two ways. The first option is to increase the number of periods along the x-direction, Nx, since a pure BIC with an infinitely high Q-factor assumes an infinite number of periods. Thus, more periods result in higher Q-factor53. The other way is to reduce the fabrication imperfection, such as side wall roughness of Si pillars and tapering, which increases scattering loss and results in the degradation of the resonance quality.

In summary, we demonstrate the observation of unique type of FP-BIC modes supported at the edge of truncated 2DPhC composed of Si pillars in square lattice structures for a near-IR wavelength range from 1400 to 1500 nm. The edge BICs are supported by the Si pillars of larger diameter in the terminating layer than that of host 2DPhC. The Q-factor and resonance wavelength can be tuned by a nanometer-thick alumina layer conformally deposited by ALD. The fine-tuning of quasi-BIC results in an improved Q-factor by over 60 % and a red-shift of the resonance wavelength. These features can be used for surface sensing and refractometric sensing in the detection of biomarkers.

Methods

Theoretical analysis

The photonic band diagram in 2D (Fig. 2a) was simulated by MIT Photonic-Bands (MPB) software package54. The band diagram and Q-factors in terms of wavevector (Fig. 2b and c) were calculated by finite element method with COMSOL (COMSOL, Inc). The transmission spectra (Fig. 2d, Supplementary Figs. S2 and S5) and electrical field profile (Fig. 2e) were calculated, using Lumerical (Lumerical FDTD solutions from Lumerical Inc.) software based on finite-difference time-domain (FDTD) method with mesh size of 2 nm. The refractive indices of Si and SiO2 are 3.48 and 1.46, respectively. Note that the transmission spectra in Fig. 2d is normalized to the maximum one.

Sample fabrication

Truncated photonic crystal structures were fabricated by electron beam lithography and reactive ion etching (RIE) on an SOI (silicon on insulator) wafer with a 1.5 μm silicon device layer on top of a buried, 2 μm thick, silica layer (Supplementary Fig. S7). The wafers were acquired from Siegert Wafer GmbH (Germany). The device layer consists of <100 > crystalline p-type silicon with a specified resistivity of 1-5 Ohm-cm. The wafer was prepared for electron beam exposure by spin-coating a 180 nm layer of CSAR positive resist (AR-P 6200, Allresist GmbH, Germany) followed by thermal evaporation of a 20 nm aluminum discharge layer. The desired pattern was exposed using a JEOL JBX-9500FS electron beam lithography system with a dose of 350 μC/cm2. The discharge layer was stripped in TMAH developer, AZ 726 MIF (Merck, Germany), subsequently developed using developer, AR 600-546 (Allresist GmbH, Germany) for 90 seconds. A new 20 nm aluminum layer was deposited using e-beam evaporation. A lift-off process was carried out (Microposit Remover 1165) to remove the CSAR resist, leaving the aluminum layer with the desired pattern as a mask for the subsequent dry etch.

RIE using SPTS-Pegasus etcher was done using a single processing step with a mix of etching gas (SF6 at 44 sccm) and passivation gas (C4F8 at 77 sccm). The etch process lasted for 5–6 minutes with a coil power of 1000 W and a platen power of 20 W until the buried oxide was reached and the silicon device layer was fully removed. The processing parameters were then changed (40 sccm C4F8, 5 sccm O2, coil power 1100 W, platen power 180 W) in order to etch into the oxide for 2 min by STS-MESC Multiplex ICP etcher, giving an etch depth of approximately 900 nm (Supplementary Fig. S1). Afterwards, the remaining aluminum mask was removed using TMAH developer.

Alumina layers of ta = 2.5, 4.7, and 7.3 nm were conformally deposited on samples by the atomic layer deposition (ALD) technique by 25, 50, and 75 cycles, respectively (Fig. 4). Their thickness is measured by an ellipsometer on a flat Si substrate deposited at the same time as 2DPhC samples.

Transmission measurement

The experimental setup is shown in Fig. S8 of Supplementary Information. Supercontinuum light from the broadband laser (SuperK; NKT Photonics A/S, Birkerød, Denmark, emission wavelength: λ = 350–2400 nm) was coupled to the Si ridge waveguide at the cleaved edge of Si chip by end-fire coupling through a single mode polarization maintaining (PM) fiber. The transmitted light are out-coupled from the other end of Si ridge waveguide through another single-mode PM fiber and detected by the optical spectrum analyser (OSA, Ando AQ-6315E; Yokogawa Electric Corp. Tokyo, Japan, detection wavelength range: λ = 500–1750 nm) with the wavelength steps of 0.4 nm for Figs. 3, 4 and 0.6 nm for Supplementary Fig. S3, respectively. The baseline transmission was taken from the transmission spectrum through the Si waveguide with the same length but without the photonic crystal part, which was then used to normalize the measured transmission from the samples in Figs. 3, 4, and Supplementary Fig. S3.