Introduction

Soon after the original proposal of Josephson in 19621, it became clear that the Josephson effects are typical not only to tunnel junctions2, 3, but to many other types of so-called weak links. Those are the areas of a system (superconducting or superfluid) with the size of the order of the healing length, where the system’s order parameter is substantially suppressed4, 5. The actual sizes of weak links in various systems may drastically vary, from a few nm in the case of a superconducting tunnel junction3 up to 10–100 nm for Dayem bridges6, and even microns in the case of a normal-metal barrier7. Another example of a system exhibiting Josephson tunneling is liquid He flowing through an array of microapertures8, 9. In such a system, if a pressure is imposed on one side, counter-intuitively the superflow ceases to show mass transport and starts to oscillate. If the healing length drops as the temperature is lowered much below critical, the oscillatory sinusoidal current-phase relation connecting the two sides of the weak link gives way to a linear dependence10, 11. In atomic systems, the Josephson phenomena have been extensively studied for double-well potential traps, where a barrier separating the two Bose-Einstein condensates (BECs)12,13,14,15,16,17,18 provides the mechanism of coupling their order parameters. A similar setting has been realised in ultracold Fermi gas mixtures close to a Feshbach resonance, which unite Bose-Einstein condensation of tightly bound molecules and Bardeen-Cooper-Schrieffer superfluidity of long-range fermion pairs19.

It has been argued, however, that coherent oscillations in double-well-confined BECs may be regarded as the a.c. Josephson effect and such a setting can be reasonably called a Josephson junction only in the case when there is no confinement by the two sides of the barrier, i.e. in the limit of an infinite system20, or when the barrier is high enough to suppress the order parameter to zero17. The closest approximation of such a system can be realised by connecting the two wells in a ring geometry. Ring-shaped and toroidal atomic BECs with a weak link have been considered21,22,23, with the main focus on the investigation of the interplay of quantum fluctuations and tunneling of bosons through the junction. Atomic-BEC rings with a rotating weak link have been shown to exhibit quantum phase slips between quantized persistent current states24,25,26 including the hysteresis between the neighbouring linear current-phase branches27. In this case, due to the relatively large size of the barrier, only the hydrodynamic regime of the weak link has been reached28. Recently, finite-circulation states in a tunable array of tunneling weak links in a ring-shaped superfluid have been realised to reveal the effect of several junctions on the stability of the atomic flow29.

Another system that has come into focus for bosonic Josephson effects and realisation of supercurrents is that of exciton-polaritons, solid-state quasiparticles stemming from the strong coupling of excitons in a semiconductor and photons in a microcavity30. In polariton systems, the observation of oscillations (akin to a.c. Josephson effect) due to an imbalance of population between double-well-connected polariton BECs was observed under pulsed excitation31, 32. Still, no characteristic current-phase relation has been reported, and, for a barrier size comparable with the system size, this interconversion of the two BECs can more simply be interpreted as nonlinear Rabi oscillations in a coherent two-level system. At the same time, based on this progress and the mathematical analogy with superconducting flux qubits, split-ring polariton condensates have been proposed33, 34. The nontrivial topology of the ring-shaped BECs together with the uniformity of the potential along the ring circumference makes them an ideal system for investigating persistent currents and superfluid properties of polaritons. However, to date the experimental realisations of circulating polariton currents35,36,37,38 were only achieved in the settings with a broken chiral symmetry without the study of a possible weak-link behavior. Compared to atomic BECs where different regimes of a weak link in a ring can be studied by rotation of the cloud25—or, alternatively, rotation of the barrier24, 27, 28,—in solid-state condensates, such as exciton-polaritons, rotation of the particle ensemble or the weak link around a ring is hard to achieve due to the very short lifetime of such condensates. Recently, however, ultrafast temporal modulation techinques enabled for the striking demonstration of optical stirring of polariton condensates and for observation of Floquet-Bloch bands39,40,41.

Here, we demonstrate the first all-optical realisation of a ring Josephson junction within a solid-state platform of exciton-polaritons. The boundary conditions on the weak link and the supercurrent flowing through it are defined by obstructing one part of the ring from an externally imposed flow of particles otherwise present in both branches of the same ring. In this way we can exert an effective circulation akin to a moving barrier in a static ring. In our experiments, as the barrier is changed from a vanishingly thin to a thick one, the phase difference Δϕ across the weak link changes, and so does the velocity of superflow under the barrier v which is proportional to this phase difference. For Δϕ lower than π, v is lower than the sound velocity cs and the fluid behaves as a superfluid, with a continuously connected phase across the barrier. Phase slips leading to the appearance of a winding around the ring in this regime cannot happen as this would increase the system’s energy. However, for circulations that bring v close to cs, the phase difference across the barrier approaches π and it is energetically more favourable to reduce the amplitude of the order parameter within the barrier. At critical circulations, a true Josephson junction is formed with zero density across the barrier and phase discontinuity at its extremes. This state will be described in our theoretical model with the appearance of two degenerate minima in the system’s free energy landscape. This leads to two possible outcomes of the same-setting experiment: one with zero and one with non-zero quantized circulation of phase gradient around the ring. As a result, when experiments are repeated many times, supercurrent states created in many realisations form statistics of zero and non-zero windings of phase. These are key conditions for establishing of the Josephson regime. Here, a sinusoidal behaviour of the tunneling current versus applied circulation is demonstrated while the hydrodynamic flow is suppressed. For even larger barriers, Δϕ exceeds π and the order parameter in the region of the weak link is forced to reconnect again, recovering the hydrodynamic regime with velocity circulation increased by one quantum number. Our experiments provide direct evidence of the switching between hydrodynamic and Josephson regimes in an exciton-polaritons quantum fluid.

Results

Annular polariton BEC with imposed circulation

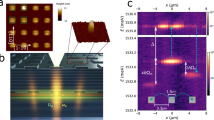
Exciton-polaritons present a powerful platform to study collective phenomena in the solid state. They are endowed with interactions inherited from their exciton component and, at the same time, they have a light effective mass and high degree of spatial and temporal coherence thanks to the underlying photons42. Furthermore, the driven-dissipative nature of polariton systems leads to the high accessibility and control over both the excitation and readout, allowing for optical shaping of such superfluids into desired configurations42, 43. Here, as shown in Fig. 1a, we form the annular polariton condensate by the continuous-wave pumping laser of a Mexican-hat profile that provides conditions for polaritons to reach the threshold density at the bottom of the potential. The polariton condensate is coherent along the whole ring, allowing the measurements of density (Fig. 1b) and phase (Fig. 1c) with interferometric techniques (see Methods for details). The phase profile shown in Fig. 1d highlights the phase gradient, which corresponds to a finite velocity from the top to the bottom of the ring. This is caused by a wedge in the cavity thickness (see the Supplementary Information, SI), accelerating polaritons in the direction of the wedge44, 45. Despite this, the net circulation along the ring remains zero, with the flow on one side compensating the flow on the other. However, when the flow in one part of the ring is suppressed by the presence of a barrier, the steady state which is created as a result exhibits a non-zero net circulation. To create a tunable barrier, we employ a second non-resonant laser to locally blueshift the polariton potential. This all-optical modulation is proportional to the intensity of the second laser and results from the repulsion between polaritons and the exciton reservoir cloud. The schematic of such tilted polariton ring with an imbalance of flows along the two arms is shown in Fig. 2a, along with an electric-circuit analog in Fig. 2b. By varying the position of the optically-created barrier and changing its power, we span a large range of circulations from negative to positive values. Figure 2c, d show examples of experimental density and phase profiles created on the polariton ring when the barrier is placed on the left (c) and on the right (d) sides of the ring.

Fig. 1: Polariton ring with an imposed flow.
figure 1

a Schematic of the non-resonant pump profile (red) creating the potential confining the polariton BEC (blue). Dimensions of the pump are given on the panel. b Experimental steady-state PL image of a ring-shaped polariton condensate in the uninterrupted case, and (c) the corresponding phase distribution dictated by the microcavity wedge. d Experimental density (blue) and phase (red) profiles of the annular polariton BEC with imposed flow, taken along the red dashed line in panel (c), counter-clockwise with the zero of azimuthal angle chosen at the top of the ring (bold red point). While the density is almost uniform, the linear slopes of the phase along the two halves of the ring reveal two supercurrents flowing in opposite directions, that results in a total circulation equal to zero.

Full size image
Fig. 2: Controllable imposed circulation along the tilted polariton ring-shaped BEC.
figure 2

a Sketch of the tilted (due to the microcavity wedge) polariton ring interrupted on the right-hand side by a weak link of effective width d. The yellow lines show the direction of the flow k. The red arrow marked Etun illustrates the tunneling energy (see text). b An electric-circuit analog of the experiment: a current-biased ring with the Josephson junction placed on the right arm. The black arrows indicate the direction of the current Ibias. The gray circular arrow indicates the azimuthal angle axis. c, d Exemplary density (blue) and phase (red) profiles along the central radius of the ring, for the barrier of power 5 mW placed on the left side (c) and the barrier of power 20 mW placed on the right side (d) of the ring. The insets show the experimental 2D intensity profiles for these cases. e, f The corresponding distributions of k according to Eq. (1) and the average imposed circulations (given on top of the panels) provided by the chosen barriers. By choosing the position of the barrier (left or right) and varying the power from 3 mW to 20 mW for each position we span a wide range of 〈k〉 from negative to positive values.

Full size image

In a steady state, the order parameter of the condensate must have the form \(\psi (\theta )=\sqrt{\rho (\theta )}{e}^{i\phi (\theta )}\), where ρ is the superfluid density and ϕ is the phase. The average imposed circulation 〈k〉 can be calculated for each given realisation by decomposing the experimental profiles ψ(θ) into plane waves as:

$$\langle k\rangle=\sum | {W}_{k}{| }^{2}k,\qquad {W}_{k} \sim \mathop{\int}\limits_{0}^{2\pi }\sqrt{\rho (\theta )}{e}^{i\phi (\theta )}{e}^{-ik\theta }d\theta .$$
(1)

Since the variable θ represents azimuthal angle, k are dimensionless and represent the angular momentum eigenstate numbers in such a decomposition. In Fig. 2e, f we show examples for specific realisations (those given in Fig. 2c, d) and the corresponding average externally-imposed circulations 〈k〉. They change from realisation to realisation. More examples of experimental profiles for various barrier positions and powers, and the corresponding decompositions (1) are provided in Supplementary Fig. 3.

Two regimes of the polariton weak link

The external circulation along the free part of the ring creates a phase difference Δϕ across the barrier region, resulting in a velocity of superflow under the barrier v ≈ (ℏ/m)Δϕ/d, where m = 0.5 × 10−4m0 is the effective mass of the particles (m0 is the free electron mass). By increasing the barrier power, we increase the absolute value of 〈k〉 and—extracting both the phase difference and the barrier width from experimental profiles—we are able to track the under-barrier flow velocity. For each experimental realisation, the phase difference and imposed current are evaluated individually, revealing the velocity-current relationship shown in Fig. 3a (it reports 4000 points corresponding to individual realisations, 500 per each barrier position and power). This comprehensive dataset provides robust statistics on the current-phase relationship across the entire range of experimental repetitions, where we are able to span a range from very small to large values of circulation in both negative and positive domain. Figure 3a unites the data taken for different barrier positions and powers; in order to analyse the data in combination, for the right-placed barriers we plotted v taking the phase difference in the opposite direction (−Δϕ).

Fig. 3: Two regimes of the weak link and the system’s free energy landscapes.
figure 3

a The under-barrier velocity versus imposed circulation. The data is united for all 〈k〉 obtained from both the left- and right-placed barriers. All data points correspond to different experimental realisations, with colors of the points indicating the hydrodynamic (blue) and Josephson (red) regimes. The black dashed line is a guide to the eye for velocity behavior in a phase slip event. The red dotted line marks the average sound velocity cs, the red-shaded range indicates the minimal and maximal values of cs estimated from variations in density (see SI). b, c Two realisations in the Josephson regime obtained for the 10 mW right-placed barrier, one of which shows zero winding (the dashed red line in (b) and the left phase map in (c)) and the other winding 1 (the solid red line in (b) and the right phase map in (c)). The gray-shaded area shows the barrier region. d–f Enlarged views of the under-barrier density for realisations corresponding to different regimes. In particular, (e) is a zoom of (b), with the two lines corresponding to the realisations with zero (dashed) and non-zero (solid) windings. For both lines, the density touches zero under the barrier creating the condition for a phase jump. d, f Similar regions for the density profiles taken in the hydrodynamic regime at low and high 〈k〉 (see the rhombus and circle symbols in (a)). In this regime the density under the barrier does not go to zero. g The system’s free energy according to Eq. (3) for selected realisations (see the SI), revealing the changing “washboard” potentials. For small imposed circulations, the global minimum corresponds to no winding (top blue). For the barrier realisations resulting in ∣〈k〉∣ in the critical range (the red points in a), some realisations of the same-setting experiment provide the minimum close to Δϕ = − π (the dashed dark-red line, w = 0) and others at Δϕ = π (the solid dark-red line, w = 1), forming statistics among realisations. At further increase of 〈k〉, the minimum at Δϕ = π corresponding to w = 1 prevails at all times (bottom blue).

Full size image

For small powers, as long as the order parameter is not fully suppressed in the barrier region, the phase does not have room for ambiguity due to single-valuedness of ψ. This is the hydrodynamic regime, in which the phase difference across the barrier is bound to compensate for the flow along the opposite side of the ring. An example of the phase and density profiles in this regime is given in Fig. 2c. However, when ∣〈k〉∣ is increased, we clearly see in Fig. 3a that the data points start deviating from the linear hydrodynamic dependence. When the phase difference imposed on the barrier reaches π, within the repeated realisations of the same experiment we start to register stochastic sharp phase jumps in the weak-link region that reverse the direction of the under-barrier flow (see the red data points in Fig. 3a, which upon reaching a critical velocity experience a drop to negative values, creating two plateaus in an extended range of 〈k〉). Example of the density and phase profiles corresponding to this regime are shown in Fig. 3b, c: whereas the density distribution along the ring stays practically unchanged, the phase profiles can randomly show the absence or presence of a non-zero winding, for the same position and same power of the barrier. We find that the critical velocity of the under-barrier flow that is reached when the behaviour of the weak link is changing (see the red dotted line in Fig. 3a) is approximately equal to the sound velocity \({c}_{{\rm{s}}}=\sqrt{gn/m}\approx 0.63\,\mu {\rm{m}}/{\rm{ps}}\), with n denoting the average condensate density and g the polariton interaction constant. To account for fluctuations in condensate densities across different realizations and barrier powers (see SI), the sound velocity in Fig. 3a is shown with a corresponding variability range (the red-shaded range of velocities). At further increase of ∣〈k〉∣ the system exhibits a phase slip: the phase difference created by the external circulation is decreased by 2π. If we keep increasing the power of the barrier, the hydrodynamic regime is recovered (blue data points in the region of large ∣〈k〉∣ in Fig. 3a). At this point, the under-barrier superflow velocity starts to grow again linearly with Δϕ, but with a non-zero winding of phase around the ring (w = ± 1 for barriers on the right and left, respectively).

Since it is apparent from Fig. 3a that in the critical range of imposed circulations the dependence v(〈k〉) is multi-valued, in order to accurately distinguish between the situations when the weak link is hydrodynamic and when it realises a Josephson junction, we take a look at the behavior of the order parameter in the weak-link region. Figure 3d–f show such regions enlarged, for four realisations in different regimes that correspond to chosen points on the velocity panel a. As predicted, in the hydrodynamic regime the wavefunction is connected everywhere (Fig. 3d), supporting the superflow along the ring circumference. When the critical velocity is reached, however, we observe that the density under the barrier goes to exact zero in one point (Fig. 3e), breaking the continuity and creating the condition for stochastic phase jumps (see SI for more details). The superfluid motion in the weak link region in this regime is suppressed. Importantly, as demonstrated in Fig. 3f, when the hydrodynamic regime is restored for a higher barrier power, we see the reappearance of a fully connected phase and non-zero order parameter.

An important feature of our experiments is that both the barrier and the ring condensate are all-optically generated by external lasers. Although fluctuations in the laser intensities lead to variations in the barrier width and polariton densities (see Supplementary Fig. 2), there is no associated error in the evaluation of individual points in Fig. 3a, as both the average 〈k〉 and the phase difference are extracted independently for each experimental point. The effect of these fluctuations is therefore visible in the distribution of the whole dataset shown in Fig. 3a: despite the spread of points, the current-phase relationship remains clearly visible.

System’s free energy landscapes

As Josephson pointed out for superconductors46, for a system which is interrupted by a barrier, the free energy of the system

$${\mathcal{E}}[\psi ]=\oint Rd\theta \left[-\frac{{\hslash }^{2}}{2m{R}^{2}}{\psi }^{*}\frac{{d}^{2}}{d{\theta }^{2}}\psi+\frac{g}{2}| \psi {| }^{4}+(U(\theta )-\mu )| \psi {| }^{2}\right]$$
(2)

contains a contribution from the barrier region, which depends on the phases of the order parameter ψ by the two sides of the weak link and whose magnitude becomes greater as the barrier is made thinner. In Eq. (2), μ is the condensate chemical potential and the optically-created potential U(θ) is nonzero only in the region of the weak link. We use an equilibrium, zero-temperature model, similar to that applied in superconductors and atomic gases. While the system is driven-dissipative, the long polariton lifetime (100 ps) allows the effect of dissipation to be neglected in our steady-state observations. As we show below, this model provides a good correspondence with the experiment. The line integral in Eq. (2) is to be taken around the red dashed line in e.g. Fig. 3c, which can be split without the loss of generality into the barrier region of the width d and the remainder of the ring of the length L = 2πR − d, such that ∮ = ∫L + ∫d. The last term in this sum represents the part of the free energy from the barrier Etun similar to the one described by Josephson. Then, to gain insight into the role of external circulation 〈k〉 imposed on the polariton ring, we consider an approximation where along the free part of the ring the coherent condensate wave function has a uniform density and a linearly changing phase (including the own phase and the one from the imposed motion), whereas at the barrier the wave function experiences a phase jump Δϕ. These approximations allow us to build an intuitive, minimal model that—despite its simplicity—captures the essential fundamental features of Josephson physics. Deriving the associated energy landscape in this fashion, we get the free energy in terms of the phase difference Δϕ:

$${\mathcal{E}}(\Delta \phi )={E}_{{\rm{kin}}}{(\Delta \phi )}^{2}-{E}_{{\rm{tun}}}\cos (\Delta \phi+\langle k\rangle L/R)+\,\text{const}\,,$$
(3)

where Ekin = ℏ2ρ0/(2mL) = ℏ2N/(2mL2) denotes the amplitude of the parabolic term, with ρ0 = N/L and N the number of particles in the polariton BEC. The detailed derivation is provided in Methods.

In Eq. (3), Δϕ can be treated as a coordinate and \({\mathcal{E}}(\Delta \phi )\) as the potential energy for the system’s dynamics, so that in equilibrium it is forced to stabilize in a global minimum of \({\mathcal{E}}(\Delta \phi )\). By changing the width and height of the barrier in U(θ) one can manipulate both the circulation 〈k〉 and the ratio of the amplitudes Ekin/Etun. This effectively results in the reshaping (tilting and shifting) of the free energy landscape as a function of the phase difference Δϕ across the barrier. Note that the ratio Ekin/Etun extracted from the experiments falls within the correct parameter range to enable the interplay between the two terms in (3) (see Supplementary Fig. 4a). In our experimental data, any specific realisation allows to assess Ekin/Etun by analytical fitting of the density tails in the barrier region, as well as to define the barrier width d and average 〈k〉 according to Eq. (1). The corresponding energy landscapes \({\mathcal{E}}(\Delta \phi )\) calculated per one particle (divided by N) for four chosen realisations belonging to different regimes are plotted in Fig. 3g. The calculation details are provided in the SI, together with more examples for both left and right barriers of different powers in Supplementary Fig. 4. For small imposed circulations, the free-energy landscape (top blue line in Fig. 3g) shows that the system in the steady state has to stay in the global minimum of \({\mathcal{E}}\) at Δϕ < 0, which is shifting with the growth of 〈k〉. When 〈k〉L/R approaches  − π for the left-placed barriers (or  + π for the barriers on the right) and Ekin/Etun is assuming its maximal values, the two minima of \({\mathcal{E}}(\Delta \phi )\) become shallow and close in energy (up to being degenerate). Repeated realisations of the experiment in this regime result in the statistics revealing one minimum lower than the other in some of realisations, and vice versa in the others (see the dashed and solid red lines in Fig. 3g). The dependence of Δϕ on 〈k〉 in this regime is flat, with the phase difference across the barrier being constant (with a small variance) in the vicinity of  ± π. Provided by these energy considerations, the possibility to realise two distinct values of the phase difference (equilibrate in one of the two degenerate minima of \({\mathcal{E}}\)) stochastically requires the existence of at least one point under the barrier where ρ = 0 so that the phase is undefined. This is confirmed by looking at the density behavior under the barrier, see Fig. 3e. When 〈k〉 is increased and the phase slip occurs, the minimum corresponding to a non-zero winding becomes deeper and prevails in all realisations (the bottom blue line in Fig. 3g).

Mass transport across the weak link and the tunneling current

The Josephson regime is characterized by the undefined phase inside the weak link. The experimentally observed Δϕ becomes independent of  〈k〉 within a certain range, which results in the two plateaus of the red data points in Fig. 3a. One concludes that the observed phase difference, which stays fixed while the externally-imposed value 〈k〉L/R is changing, contains a contribution from the inherent (tunneling) phase of the order parameter, \(\Delta \tilde{\phi }\). The change of this tunneling phase by the two sides of the weak link is the origin of the Josephson (tunneling) current. Since there is no bulk superflow around the ring as soon as the density touches zero under the barrier, the only current through the weak link is the Josephson current \(\propto \sin (\Delta \tilde{\phi })\). Therefore, in this regime we expect the periodic change of the under-barrier current versus the imposed circulation 〈k〉, which is analogous to a supercurrent in a SQUID becoming a periodic function of the magnetic flux piercing the ring47. To retrieve the Josephson current, one needs to distinguish the tunneling contribution to the phase difference from the total measured Δϕ. To do so, we use the observed shapes of the wave function in the weak link region (their analytical fitting in the under-barrier region, see Supplementary Fig. 2 for details) and, assuming for the model case a linear growth of phase along the free part of the ring, make a rigid shift by the imposed phase difference  − 〈k〉L/R in the obtained functional dependence \({j}_{\theta }={j}_{c}\sin (\Delta \phi+\langle k\rangle L/R)\) which is provided in Methods. Plotting this way the under-barrier current against the imposed circulation 〈k〉 in Fig. 4a, we thereby confirm that the experimental points corresponding to the Josephson regime show periodic sinusoidal behavior, while the points corresponding to the hydrodynamic regime are scattered (due to the added contribution of bulk current).

Fig. 4: Josephson current and the density imbalance at the barrier.
figure 4

a The under-barrier current \({j}_{\theta }=-{j}_{c}\sin (\Delta \phi+\langle k\rangle L)\) versus applied circulation 〈k〉, with jc = j0ρ2D/d, j0 ≲ 1 ps−1 given the polariton mass m = 0.5 × 10−4m0 (see Methods for calculation details), revealing the periodic change versus 〈k〉 for the Josephson regime. The points corresponding to the hydrodynamic regime (the open circles) do not follow the sinusoidal behavior (the black dashed line), being spread around zero. b Density imbalance between the two sides of the barrier versus the average imposed circulation (absolute value). The offset due to the wedge for the non-interrupted ring is subtracted. The dashed black lines are guide to the eye indicating the independence of Δn on 〈k〉 for the realisations in the hydrodynamic regime (open-circle points) and the linear change with 〈k〉 for the Josephson regime (full-circle points). The enlarged individual groups of points are provided in Suppl. Fig. 7. Colour code of the data points in panels (a, b) is chosen to distinguish different barrier positions and powers, as given in the legend. c Probability of realisations with non-zero windings (w = ± 1) against the absolute value of average imposed circulation. d Winding numbers versus 〈k〉 for all realisations among all barriers. The color code in panels (b, d) is blue for the left- and yellow for the right-placed barriers. Gray points in (d) correspond to the case of an uninterrupted ring (without a barrier). The dashed line indicates the expected behaviour from our idealised theory for a fixed L = 7πR/4.

Full size image

Finally, we check the behavior of the density imbalance at the barrier versus the applied current in the two regimes. To do so, we extract from the density profiles in each experimental realisation the normalised imbalance Δρ = ρ(θ2) − ρ(θ1) for barriers on the right and the opposite for the left-placed barriers, and then multiply by the 2D density measured for each barrier power: Δn = ρ2DΔρ. The density imbalance is plotted against the absolute value of the applied circulation in Fig. 4b for both positions of the barrier united. Individual groups of points for each power are provided separately in the SI. One can clearly see that in the realisations corresponding to the hydrodynamic regime there is no dependence of Δn on 〈k〉. It suggests that in this regime the polaritons form a superfluid ring where the density imbalance is not dependent on the imposed flow, with the mass transport sustained along the macroscopic flow path (ring circumference). When no winding of phase is present (light- and dark-blue open points), the average imbalance is zero, while for the hydrodynamic flow with w = 1 (orange and red open points) the constant level of average Δn is shifted, indicating that the superfluid density redistributes along the ring to sustain the winding. On the other hand, for the Josephson regime (solid points of all colors) there is a clear linear trend Δn on 〈k〉 that indicates that as soon as the flow under the barrier is interrupted (ρ = 0 in one point), there is no mass transport across the weak link and only tunneling is allowed.

To complete the analysis, we present the Josephson junction characteristics in terms of winding-current dependence. To do so, we unite the data of observed windings versus average imposed current 〈k〉 regardless of the barrier powers. Then we extract the statistical probability to realise a non-zero winding (in our case, w = ±1) at each ∣〈k〉∣ within all 4000 frames (see the Supplementary Fig. 6 for a statistical histogram of the windings). Figure 4c reveals that this probability experiences a sharp rise in the region of ∣〈k〉∣ ∈ (0.4, 0.65), which corresponds to the imposed circulation values resulting in under-barrier velocities close to critical, in which the difference in phase of the weak link can equally be ± π (Josephson regime). In Fig. 4d, the phase winding around the ring is reported as a function of the average imposed current for each of the 4000 realisations, showing the jump between quantised levels corresponding to angular momentum  −1, 0 and  +1.

In conclusion, we have demonstrated that the characteristic features of a weak link in a ring geometry can be measured in a photonic setting leveraging the nonlinear behavior of exciton-polaritons. Even while the optical pumping introduces some level of experimental noise, the Josephson physics that we report here is very robust to such fluctuations. Notably, the current-density relation derived from the density and phase of the quantum fluid shows a quantitative correspondence with the minimalistic zero-temperature equilibrium model, formulated in terms of an energy functional and analogous to that of superconductors. This underlines that exciton-polariton platform, despite being inherently driven-dissipative, indeed belongs to the class of systems displaying the fundamental Josephson-junction behavior. While superconductor rings are crucial for high-precision measurements of magnetic fields (SQUIDs) or for generation of stable voltages (Josephson voltage standard), and superfluid helium or atomic BECs in a ring geometry have been proposed for the realisation of very sensitive gyroscopes48, the driven-dissipative nature of exciton-polaritons will allow for design of new schemes of operation based on fast nonlinear optics and coherent laser excitation. Finally, despite this work having been performed at the temperature of 10K, suitable materials like transition-metal dichalcogenides49, 50 or perovskite crystals51, 52 will make it possible to operate a polariton ring Josephson junction at room temperature.

Methods

Experimental methods

The sample is a GaAs-based microcavity with 12 quantum wells embedded within two distributed Bragg reflector mirrors. The high-quality factor of the microcavity (Q = 105) allows the attainment of extended polariton lifetimes (polariton linewidth  = 0.1 meV) and it is designed to incorporate a significant wedge in the microcavity thickness of 1 μeV/μm. The Rabi coupling measures 15 meV, and the cavity-exciton detuning is  −2 meV.

The formation of the ring polariton condensate occurs under non-resonant excitation using a continuous-wave laser tuned to 735 nm (polariton resonance at 774 nm), achieved by shaping the laser profile into a Mexican-hat intensity pattern (shown schematically in Fig. 1a) that serves both as the pumping beam and a confining potential. The laser intensity is modulated using a phase-only spatial light modulator (SLM) positioned in the Fourier plane of the optical system. A conjugate gradient descent algorithm53 combined with Gerchberg-Saxton iterations was used to optimize the formation of the Mexican hat in the image plane. A telescopic system is utilized to focus the beam on the sample surface and reduce the size of the Mexican hat by a factor of 50, resulting in a polariton ring condensate with the average radius R = 11.5 microns (the inner and outer radii of the ring-shaped BEC are R1 = 8 μm and R2 = 15 μm, respectively), which is formed above the threshold density in the lowest confined mode of the potential.

The barrier used to split the annular polariton condensate consists of a second non-resonant continuous-wave laser beam tightly focused into a Gaussian spot with FWHM = 2 μm. The position of the second beam relative to the polariton ring condensate is adjusted using two external mirrors. The excitation power for the barrier laser is varied from 3 mW to 20 mW in each position.

The emission from the polariton ring condensate is collected in reflection configuration by the same imaging objective (NA = 0.5, focal length = 50 mm). A small portion of the condensate is selected in one arm of a Mach-Zehnder interferometer and used as the reference phase. The image of the ring condensate and the reference are combined at the exit of the Mach-Zehnder interferometer and imaged on the CCD detector to produce an interferogram. The phase and density information are then extracted from the interferogram using FFT as described in ref. 54.

The pump lasers are chopped at a frequency of 300 Hz with a duty cycle of 10%, leaving an open time window of 333 μs. The detector is externally triggered to synchronise the acquisition with the opening of the chopper. Both the ring and barrier pump lasers are focused on the same point on the chopper plane to cut them simultaneously. For each pump power of the barrier and side of the ring (right or left), we take 500 realisations.

Theoretical methods

To describe our system we consider a one-dimensional (1D) geometry corresponding to a thin ring of an average radius R = 11.5 μm, and assume all quantities dependent exclusively on the azimuthal angle θ (see Fig. 1b–d). The validity of the 1D approximation as compared to the full 2D treatment is addressed in the SI.

To study the influence of external circulation 〈k〉 imposed on the polariton ring, in the order parameter ψ in (2) we explicitly separate the factor containing this imposed motion: \(\psi \to \psi {e}^{i\langle k\rangle \theta }=\sqrt{\rho (\theta )}{e}^{i\tilde{\phi }(\theta )}{e}^{i\langle k\rangle \theta }\), with \(\tilde{\phi }\) denoting the own phase of the condensate independent of the external circulation. The model consists of a simple consideration in which the coherent condensate wave function along most of the ring ψ(θ ∈ [θ2, θ1]) has a uniform density ρ(θ) = ρ0 and a linearly changing phase \(\tilde{\phi }(\theta )+\langle k\rangle \theta=[\phi ({\theta }_{1})-\phi ({\theta }_{2})]\theta R/L=-\Delta \phi \theta R/L\) (here θ1,2 denote the positions of the two sides of the barrier, so that θ1 + d/R = θ2 and, given the periodicity, θ2 + L/R = θ1). Having cut the barrier region out of the whole ring in this fashion, we can think of it as of a defect of the size d on which the wave function ψbarrier has a phase jump Δϕ between the right and left sides. Then the barrier part of the energy functional (2) can be integrated to produce a function \(\propto -{E}_{{\rm{tun}}}\cos (\Delta \phi+\langle k\rangle L/R)+\,\text{const}\,\), with the tunneling energy Etun defined by the specific shape of the density in the region. At the same time, substituting \(\psi=\sqrt{{\rho }_{0}}\exp \{-i(\Delta \phi )\theta R/L\}\) to the ring part of Eq. (2), we get the free energy in terms of the phase difference Δϕ given in Eq. (3) with

$${E}_{{\rm{tun}}}\approx 2N\,\frac{R}{L}\int\limits_{{\rm{barrier}} \atop {\rm{region}}}\frac{[\mu -U(\theta )]d\theta }{1+{e}^{d/\sigma }+{e}^{(\theta -{\theta }_{1})R/\sigma }+{e}^{({\theta }_{2}-\theta )R/\sigma }},$$
(4)

where σ is the fitting parameter defined individually for each chosen experimental realisation. In Eq. (4), for the sake of analytical simplicity we assumed the slopes of the under-barrier wavefunction tails to be symmetric, which is not always the case. In the data analysis presented, those tails were fitted precisely with separate parameters σ1 and σ2. The details of this calculation and additional considerations are provided in the Supplementary Information.

Josephson current

The analytical fitting of the experimental wavefunction profiles in the barrier region allows as well to calculate the expression for the under-barrier current, which in terms of the experimentally-measured phase difference reads \({\boldsymbol{j}}=(\hslash /m){\rm{Im}}[{\psi } {\ast }\nabla \psi ]=-{{\boldsymbol{j}}}_{c}\sin \Delta \tilde{\phi }=-{{\boldsymbol{j}}}_{c}\sin (\Delta \phi+\langle k\rangle L/R)\) with

$${j}_{c}=\frac{\hslash {\rho }_{0}}{m\sigma }\,\frac{2{e}^{d/\sigma }+{e}^{(\theta -{\theta }_{1})R/\sigma }+{e}^{({\theta }_{2}-\theta )R/\sigma }}{{(1+{e}^{d/\sigma }+{e}^{(\theta -{\theta }_{1})R/\sigma }+{e}^{({\theta }_{2}-\theta )R/\sigma })}^{2}}\,\approx 0.1\,\frac{2\hslash {\rho }_{0}}{md}\approx 0.2\frac{\hslash }{m}\frac{\pi ({R}_{2}^{2}-{R}_{1}^{2})}{L}\frac{{\rho }_{{\rm{2D}}}}{d},$$
(5)

where the number prefactor is an upper-bound estimate coming from the consideration that θ ∈ [θ1, θ2], θ2 − θ1 = d/R. Additionally, to be able to plot the dependence of j on 〈k〉 in Fig. 4a from the available experimental data, we roughly assumed σ ~ d/2 (more accurately, σ depends not only on the width of U(θ), but also on its steepness and the polariton nonlinearity, i.e. it changes with the healing length).